おさらい
随時、参照してください。
確率分布からのサンプリング
これからサイコロを投げようと思うのですが、最初に確率分布からのサンプリングのお話。
例えば、
X[x_1,...,x_{1000}]\sim N(μ=0,δ=1)
というのは、1000個のデータを平均0分散1の確率分布からサンプリングする事を示します。
至極当たり前の事を書きますが、これは個々のxが0に等しい事を保証するのではなく、
個々のxが大体0だよ、という意味であります。
で、このμを別の確率分布からサンプリングしてくる事を考えます。
X[x_1,...,x_{1000}]\sim N(μ, 1) \\
μ\sim N(0, 1)
これは、Xはだいたい「だいたい0の分布からサンプルされた値」だ、と言っているわけです。
こうしたサンプリングを、概念図で書くとこんな感じになります。
(この書き方をgraphical modelと呼んだりします。)
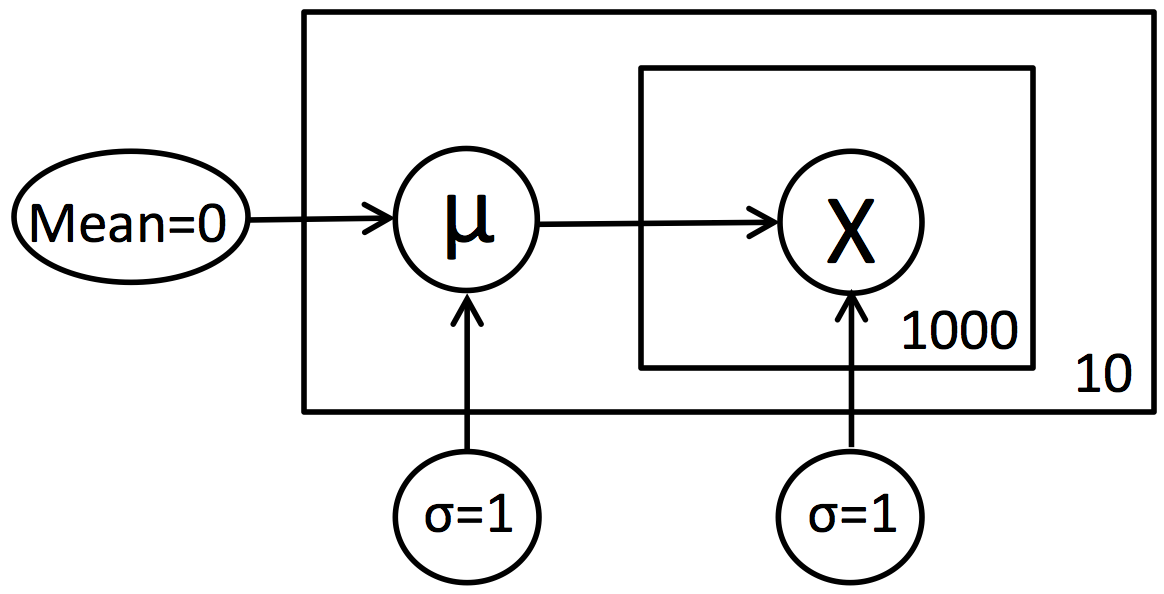
実際のXの分布がどうなるかRで描いてみます。
とりあえずXを10回ぐらい生成してみます。
set.seed(1)
N <- 10
myu <- rnorm(N, 0,1)
dat <- NULL
for(i in 1:N){
dat <- rbind(dat, cbind(i, rnorm(1000, rnorm(1, myu[i], 1), 1)))
}
dat <- data.frame(dat)
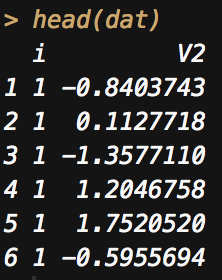
で、描画
library(ggplot2)
dat$i <- factor(dat$i)
ggplot(dat, aes(x=V2, color=i))+
geom_density(size=1.5)

与えた条件は、Xの平均の平均が0、Xの平均の分散が1、Xの分散が1の3つです。
まぁ概ね予想通りなのではないでしょうか。緑のぶっ飛んだヤツが出てくれて美味しい。
サイコロを振ろう
正六面体の理想サイコロを振るとします。
結果は多項分布になりますよね。
\frac{N!}{m_1!m_2!...m_K!}\prod_k μ_k^{m_k} \equiv Mult(m|N,μ)
μは、理想サイコロの場合、μ1~6が全て等しく1/6。
Rでとりあえず10回投げると、
set.seed(1)
rmultinom(10, 1, c(1,1,1,1,1,1))
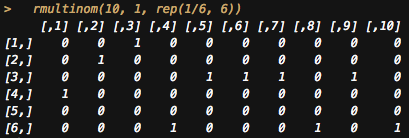
rmultinomの2番目の引数は、同時に投げるサイコロの数、です。
3番目の引数が、各面の出る偏りを示す割合を入れますが、勝手に確率にスケールしてくれます。
とりあえず1000回投げて、結果を見てみると、
set.seed(1)
dat <- rmultinom(1000, 1, c(1,1,1,1,1,1))
apply(dat, 1, sum)
1000/6=166.66..なので、まぁ概ね均一ですね。
では、1が他の面よりも3倍も出やすいイカサマサイコロを振ってみましょう。
set.seed(1)
dat <- rmultinom(1000, 1, c(3,1,1,1,1,1))
apply(dat, 1, sum)
これは、理想のイカサマサイコロですよね。
「1が他の面よりも3倍も出やすい」事が「真」だ、という意味です。
でも実際のイカサマサイコロは、この「3倍」が厳密ではなく、揺らぎを持っているわけです。
つまり、c(3,1,1,1,1,1)で与えていたμを、確率分布で与えたい。
μの分布?あ、それはディリクレ分布ですな。
\frac{Γ(a_0)}{Γ(a_1)...Γ(a_K)}\prod_k μ_k^{a_k-1} \equiv Dir(μ|a)
「1が3倍出やすいような」サイコロを100個ほど用意し、それぞれ1000回投げてみましょう。
グラフィカルモデルを書くと、こんな感じ。

ディリクレ分布の乱数は、MCMCpack::rdirichletで発生させる。
library("MCMCpack")
library("ggplot2")
library("tidyr")
set.seed(1)
N <- 100
a <- rdirichlet(N, c(3,1,1,1,1,1))
dat <- NULL
for(i in 1:N){
dat <- rbind(dat, apply(rmultinom(1000, 1, a[i,]), 1, sum))
}
dat <- data.frame(dat)
ggplot(gather(dat), aes(x=value, color=key))+
geom_density(size=2)+
xlim(0, 1000)

サイコロNo.4なんかは、面1が95/1000回しか出ていない。
が、100個のサイコロで面kが出ていた回数の分布はグラフのようになり、
全体としては面1が極端に多く出るように偏っているのが分かる。
なんというか、いい感じに偏ったイカサマサイコロを選ぶ、というのが既にギャンブルですよね。


