独立成分分析(ICA)をC++で実装してみる

初めに

独立成分分析（ICA: Independent Component Analysis) をC++で実装してみようという記事です．
間違っているところがあれば，コメントお願いします．特に記載がなければ本記事ではFastICAのことをICAと呼ぶようにします．(ICAにもいろいろあるので...)

(３年くらい前から温めていて，Githubにも載せていなかったのですが，本日高熱出して休養中なので，これを供養します)

• 2025/07/25 誤字を訂正しました

独立成分分析

ICAって何？

独立成分分析（ICA: Independent Component Analysis) とは，ざっくり言えば「混ざり合った信号」から「信号源から発せられる信号に別々に分離」することができる手法です．
初めに,以下のような信号があったとします[1]．

$$
s(t) = (s_1(t), s_2(t), ..., s_n(t))^t, t=0,1,2,...
$$

これらの信号は，干渉はしないかつ，各信号は統計的に独立であるとします．
センサなどから，得られる信号を以下のように定義します．

$$
x(t) = (x_1(t), x_2(t), ..., x_n(t))^t, t=0,1,2,...
$$

そうすると，これらは，何かしらの行列$A$で混合されているはずです．そうなると以下のように仮定できます．

$$
x(t) = As(t)
$$

ICAでは，この行列$A$を知らずに，分離しようというものです．
ただし, 元の信号$s(t)$について

• 平均は0
• モーメントは適当な次元まで発散しない

である必要があります．

今回は，復元行列$W$というものを仮定して，これを求めていくようなプログラムを書いていきたいと思います．
つまり

$$
s(t) = W^tx(t)
$$

というような$W$を求めていきます．

FastICA

ICAは一般的に，FastICA([2], [3])と呼ばれるアルゴリズムが使われるらしいです．とりあえずWikiに書いてある方法で実装してみます．

高速化？

今回は行列演算を多く行うので，速度の関係からできる限りDSP命令などを使いたいところです．めんどくさいのでライブラリを使うことにします．特に，固有値分解なんかやりたくないですね....

高貴な感じで行くなら，CBLAS/LAPACKだと思います？が，今回は手軽さをもとめてC++の行列計算といえばのEigenを選びました．

C++での実装

データのセンタリング

データのセンタリング(中心化)をします．各信号から平均値を引くだけです．
データのレンジがバラバラだと計算がしにくい(深層学習でもデータの標準化はよくやりますよね)のと，平均値は二次統計量です．今回求めたい高次統計量における独立性には，直接寄与しないはずですので，取り除いて問題ありません．

Eigenだとnumpyみたいに簡単に書けます．

void __centering() {
    mean_ = x_.rowwise().mean();
    for (int i = 0; i < rows_; i++) {
        x_.row(i).array() -= mean_(i);
    }
}

データのホワイトニング(白色化)

で次に白色化をして，無相関化します．
白色雑音とか思い受けべてもらうといいかも知れません．
ホワイトノイズは全ての周波数成分が等しいパワーで含まれる雑音のことで，その統計的性質として分散共分散行列が単位行列になること・無相関が特徴だったと思います．

ICAでは非ガウス性を最大化することで，独立成分を見つけます．したがって，白色化を行った二次統計量を取り除き，相関のない状態にしていくことで，残された依存性(高次統計量)から独立成分を見つけます．

なんかうだうだ言いましたが，やっていることは単純で，分散共分散行列を計算してその固有値と固有ベクトルを求めています．

手順ですが，以下の通りです．

void __whitening() {
    // 分散共分散行列の計算: Cov = XX^T / (n-1)
    conv_ = (x_ * x_.transpose()) / (cols_ - 1);

    // 固有値分解: Cov = EDE^T (E=>固有ベクトル行列, D=>固有値の対角行列)
    Eigen::SelfAdjointEigenSolver<Eigen::MatrixXd> eigen_solver(conv_);
    eigen_ = eigen_solver.eigenvalues();
    e_ = eigen_solver.eigenvectors();

    // 固有値の平方根の逆数を対角行列に変換 => D^(-1/2)
    d_sq_inv_ = Eigen::MatrixXd::Zero(rows_, rows_);
    for (int i = 0; i < rows_; i++) {
        d_sq_inv_(i, i) = 1.0 / std::sqrt(eigen_(i));
    }

    // ホワイトニングの行列=> W = D^(-1/2)E^T
    Eigen::MatrixXd whitening_mat_ = d_sq_inv_ * e_.transpose();

    // で，最後にかけて，ホワイトニングする
    z_ = whitening_mat_ * x_;
}

独立成分の抽出

前述したようにICAでは非ガウス性を最大化していきます．したがって，不動点アルゴリズムを使用します．

各成分を反復的に求めて，その前に見つかった成分に対して直交するようにします．そうすると，複数の独立成分が同じ方向に収束することを防ぎ，白色化空間内で互いに無相関な方向が得られるため，互いに独立した成分を順番に抽出することができます．

非線形関数としては，とりあえずwikiにtanhが載っていたので，これを使ってみます．

void __ica() {
    w_ = Eigen::MatrixXd(sigs_, rows_);

    for (int c = 0; c < sigs_; c++) {
        // ランダムな初期重みベクトル
        Eigen::VectorXd w = Eigen::VectorXd::Random(rows_);
        w.normalize();

        // 反復計算
        for (int iter = 0; iter < max_iter_; iter++) {
            Eigen::VectorXd w_prv = w;

            // g(x) = tanh(x)
            Eigen::VectorXd wx = w.transpose() * z_;
            Eigen::VectorXd g_wx(cols_);
            Eigen::VectorXd g_p_wx(cols_);

            for (int j = 0; j < cols_; j++) {
                // tanhとその導関数tanh'(x) = 1 - tanh^2(x)を適用する
                g_wx(j) = std::tanh(wx(j));
                g_p_wx(j) = 1.0 - std::pow(std::tanh(wx(j)), 2);
            }

            // 重みベクトルの更新
            w = (z_ * g_wx) / cols_ - (g_p_wx.mean() * w);

            // ベクトルを直交化
            if (c > 0) {
                Eigen::MatrixXd proj = Eigen::MatrixXd::Zero(rows_, rows_);
                for (int i = 0; i < c; i++) {
                    proj += w_.row(i).transpose() * w_.row(i);
                }
                w = w - proj * w;
            }

            w.normalize();

            // 距離見て, toleより小さいなら収束したと判定
            double d = std::abs(1.0 - std::abs(w.dot(w_prv)));
            if (d < tole_) {
                break;
            }

            if (iter == max_iter_ - 1) {
                // TODO: warn log
                std::cerr << "Component " << c + 1 << " did not converge."
                          << std::endl;
            }
        }

        // 収束したやつをとっておく
        w_.row(c) = w.transpose();
    }
}

計算結果

上記までにも求めたものたちを掛け合わせればOKです！

y_ = w_ * z_;

ちなみに求めた混合行列を得るには

// 固有値の平方根を対角行列に変換=> D^(1/2)
Eigen::MatrixXd d_sq = Eigen::MatrixXd::Zero(rows_, rows_);
for (int i = 0; i < rows_; i++) {
    d_sq(i, i) = std::sqrt(eigen_(i));
}

// 混合行列の推定=> A = ED^(1/2)W^(-1)
// だけど，この行列は元の混合行列の推定値であり，スケーリングと順序が異なる場合がある (ICAはこうゆうもん)
transform_ = e_ * d_sq * w_.inverse();

とすれば良いです．

完成したやつ

殴り書きしたコードなので汚いですが，一応公開します.
https://github.com/KikuchiTomo/FastICA

開発環境

• OS : MacOS
• コンパイラ : G++ (と思ったけどMacなのでapple clangです...エイリアスはるな!)
• C++ : c++11

実行結果

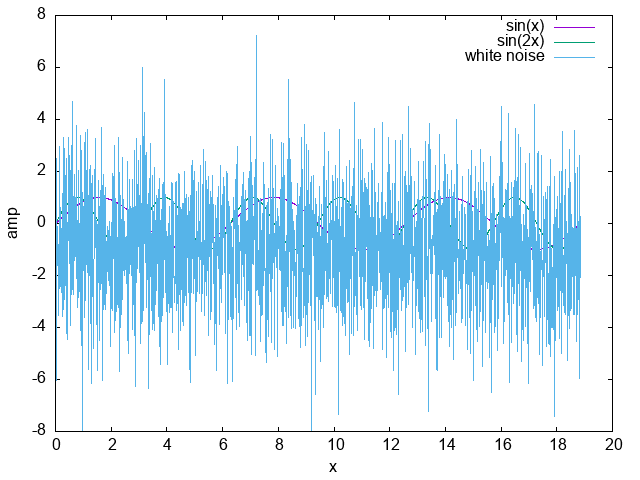
元の信号

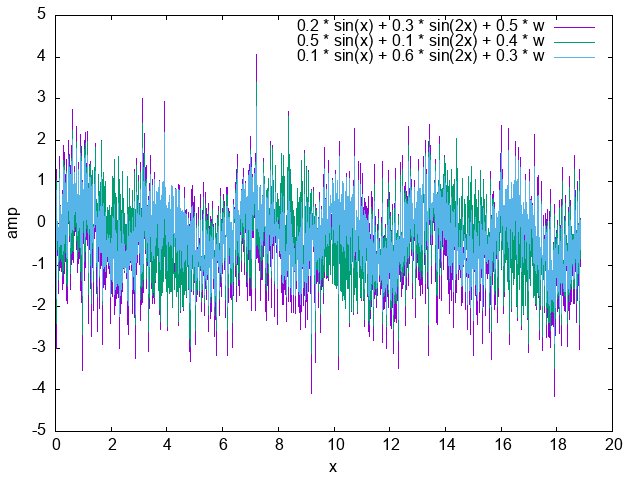
混ぜたやつ

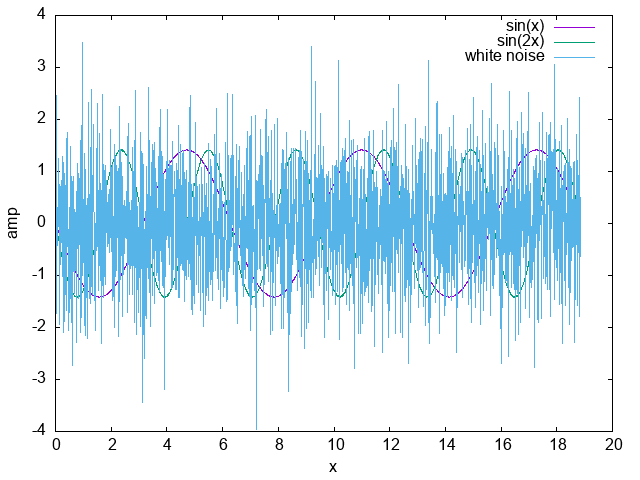
復元信号

なんか良さそうですね．

〜 FIN 〜

参考文献

[1] 村田昇, 入門　独立成分分析, 東京電機大学出版局，pp28-30, 2005．
[2] Hyvärinen, A.; Oja, E. (2000). "Independent component analysis: Algorithms and applications" (PDF). Neural Networks. 13 (4–5): 411–430. CiteSeerX 10.1.1.79.7003. doi:10.1016/S0893-6080(00)00026-5. PMID 10946390.
[3] Hyvarinen, A. (1999). "Fast and robust fixed-point algorithms for independent component analysis" (PDF). IEEE Transactions on Neural Networks. 10 (3): 626–634. CiteSeerX 10.1.1.297.8229. doi:10.1109/72.761722. PMID 18252563.
[4] FastICA, Wikipedia, 2022/06/28, https://en.wikipedia.org/wiki/FastICA#cite_note-Hyvarinen-1