ガンマ分布
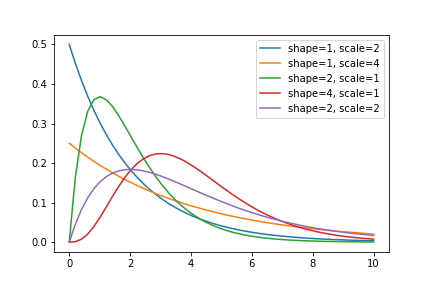
ガンマ分布は正の連続値をとる値のモデリングに使われる。
パラメータは2つあるが、ライブラリによって微妙に定義が違ったり、平均値、分散がどの程度になるか分かりづらく、いつも調べている気がするので、まとめておく。
確率密度関数
\begin{align}
f(x) &= \frac{1}{\Gamma(k) \theta^k} x^{k-1} e^{- \frac{x}{\theta}} \\
&= \frac{\lambda^k}{\Gamma(k)} x^{k-1} e^{- \lambda x}
\end{align}
$k$: shape parameter
$\theta$: scale parameter
いずれも正の値をもつパラメータである。
ただし、ライブラリによっては、$\lambda = \frac{1}{\theta}$を使って表す場合もある。
統計量
平均 $\mu= k \theta = \frac{k}{\lambda}$
分散 $v = k \theta^2 = \frac{k}{\lambda^2}$
逆に、平均、分散からパラメータを決めたい場合は、こちらを用いる。
$\theta = \frac{v}{\mu} \ (\lambda = \frac{\mu}{v})$
$k = \frac{\mu^2}{v}$
各ライブラリでのパラメータ指定方法
まとめるとこんな感じ。この表が書きたかった!
ライブラリ | shape parameter | scale parameter |
--- | --- | --- | ---
numpy.random.gamma | $k$ | $\theta$ |
scipy.stats.gamma | $a$ | $\theta$ |
PyMC3(pm.Gamma) | $\alpha$ | $1 / \beta$ |
TensorFlow Probability (tfp.Gamma)) | concentration | 1/rate |
Stan (gamma) | $\alpha$ | $1 / \beta$ |
R (rgamma) | shape | scale, 1/rate|
numpy, scipyはscale parameter $\theta$ を採用しているが、PyMC3, Stan TFPなどいわゆる確率的プログラミング言語では $\theta$ の逆数での指定となっている。
$\theta$の逆数$\lambda$はrate parameterと呼ばれ、パラメータを$\alpha, \beta$と呼んでいるライブラリでは、$\lambda$による定義を採用しているようだ。
なお、PyMC3では平均(mu), 標準偏差(sigma)でガンマ分布を指定することも可能。
また、Rではshape, rateのいずれでも指定できるようだ。
実装の確認
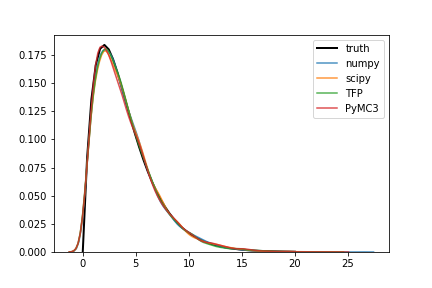
上記のパラメータ一覧が正しいか確認するため、各ライブラリで $Gamma(2, 2)$ から1万個の乱数を取得、確率密度関数を推定して比較してみた。
import numpy as np
import scipy as sp
import pymc3 as pm
import tensorflow_probability as tfp
import pystan
import matplotlib.pyplot as plt
import seaborn as sns
shape = 2
scale = 2
rate = 1 / scale
n_sample = 10000
xx = np.linspace(0, 20)
# ground truth
gamma_pdf = sp.stats.gamma(a=shape, scale=scale).pdf
s_np = np.random.gamma(shape=shape, scale=scale, size=n_sample)
s_sp = sp.stats.gamma(a=shape, scale=scale).rvs(size=n_sample)
s_tfp = tfp.distributions.Gamma(concentration=shape, rate=rate).sample(n_sample).numpy()
s_pm = pm.Gamma.dist(alpha=shape, beta=rate).random(size=n_sample)
fig, ax = plt.subplots()
ax.plot(xx, gamma_pdf(xx), label='truth', lw=2, c='k')
sns.kdeplot(s_np, ax=ax, label='numpy', alpha=0.8)
sns.kdeplot(s_sp, ax=ax, label='scipy', alpha=0.8)
sns.kdeplot(s_tfp, ax=ax, label='TFP', alpha=0.8)
sns.kdeplot(s_pm, ax=ax, label='PyMC3', alpha=0.8)
結果は下図の通りで、どのライブラリでも正しく実装できていることが確認できた。
Stanだけは確率分布から直接乱数を得る方法が分からなかったので、代わりに上記で得た乱数からガンマ分布のパラメータを推定してみた。
stan_code = '''
data {
int N;
vector<lower=0>[N] Y;
}
parameters {
real<lower=0> shape;
real<lower=0> rate;
}
model {
Y ~ gamma(shape, rate);
}
'''
data = dict(N=n_sample, Y=s_np)
stan_model = pystan.StanModel(model_code=stan_code)
fit = stan_model.sampling(data=data)
print(fit)
shape, rateパラメータの推定値はそれぞれ、1.98, 0.49となり、こちらも期待通りの結果となっている。
Inference for Stan model: anon_model_6a5d60bed963727c801dc434b96a49a1.
4 chains, each with iter=2000; warmup=1000; thin=1;
post-warmup draws per chain=1000, total post-warmup draws=4000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
shape 1.98 8.3e-4 0.03 1.93 1.97 1.98 2.0 2.04 1016 1.0
rate 0.49 2.3e-4 7.4e-3 0.47 0.48 0.49 0.49 0.5 1020 1.0
lp__ -2.3e4 0.03 1.01 -2.3e4 -2.3e4 -2.3e4 -2.3e4 -2.3e4 1192 1.0
平均、標準偏差による分布の指定
平均、標準偏差から、該当するガンマ分布のshape, scaleを計算する関数を用意しておくと便利。
def calc_gamma_param(mu, sigma):
return (mu / sigma)**2, sigma**2 / mu
mu, sigma = 4, 2
shape, scale = calc_gamma_param(mu, sigma)
def plot_gamma(xx, shape, scale):
plt.plot(xx, sp.stats.gamma(a=shape, scale=scale).pdf(xx), label=f'shape={shape}, scale={scale}')
xx = np.linspace(0, 10)
plot_gamma(xx, shape, scale)
plt.legend()
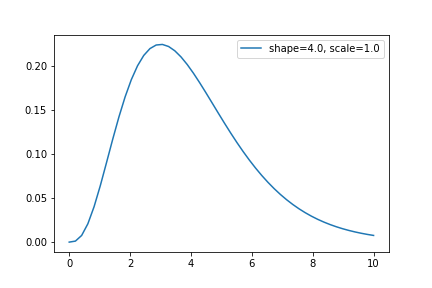
平均4、標準偏差2のガンマ分布。右に裾が長い分布なので、最頻値(最も確率が高い値)は平均値より小さくなることに注意。
おまけ:他の確率分布との関係
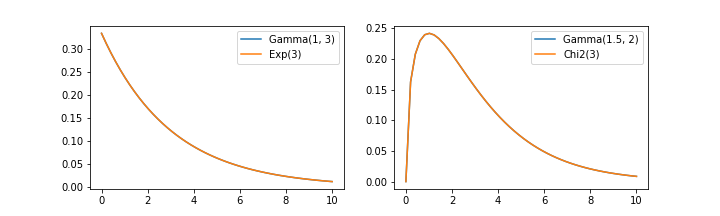
$k = 1$の時、ガンマ分布はパラメータ$\theta$の指数分布と一致する。
$k = \frac{n}{2}(n=1,2,\dots),\ \theta=2$ の時、ガンマ分布は自由度$n$のカイ二乗分布と一致する。
コードはこちら。
from scipy import stats
xx = np.linspace(0, 10)
fig, ax = plt.subplots(1, 2, figsize=(10, 3))
shape, scale = 1, 3
ax[0].plot(xx, stats.gamma(a=shape, scale=scale).pdf(xx), label=f'Gamma({shape}, {scale})')
ax[0].plot(xx, stats.expon(scale=scale).pdf(xx), label=f'Exp({scale})')
ax[0].legend()
shape, scale = 3/2, 2
ax[1].plot(xx, stats.gamma(a=shape, scale=scale).pdf(xx), label=f'Gamma({shape}, {scale})')
ax[1].plot(xx, stats.chi2(df=2*shape).pdf(xx), label=f'Chi2({int(2*shape)})')
ax[1].legend()
plt.savefig('gamma_exp_chi2.png')