概要
PRML第8章グラフィカルモデル,8.3.3 例:画像のノイズ除去をPythonで実装
コードと実験結果をまとめたJupyter notebook.
グラフィカルモデル
確率的グラフィカルモデル(probabilistic graohical model)は確率分布の図式的表現である.グラフィカルモデルを解析に用いることで,確率変数間の依存関係を直観的に読み取ることができる.
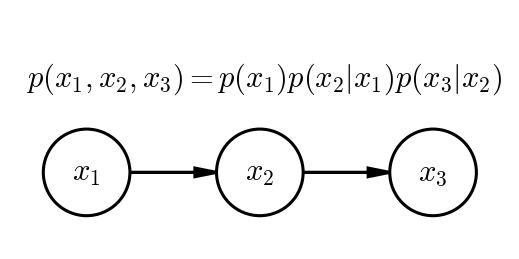
上の図は,確率分布$p(x_{1}, x_{2}, x_{3}) = p(x_{1})p(x_{2}|x_{1})p(x_{3}|x_{2})$を__有向グラフ(ベイジアンネット)で表したものである.頂点を__ノード,辺を__リンク__と呼ぶ.
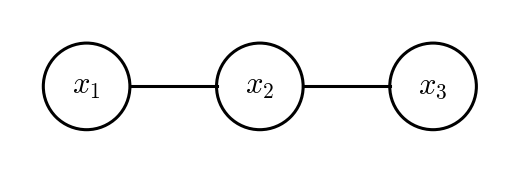
上の図は,同じ確率分布を__無向グラフ(マルコフ確率場)で表したものである.無向グラフィカルモデルでは,リンクされたノードの集合を__クリーク(clique)と呼ぶ.上の図では$\{x_{1}, x_{2}\}, \{x_{2}, x_{3}\}$がクリークとなる.無向グラフは確率分布をクリークC上の__ポテンシャル関数__$\psi_{C}(\mathbf{x}_{C})$の積の形で表す.
$$ p(\mathbf{X}) = \frac{1}{Z}\prod_{C}{\psi_{C}(\mathbf{x}_{C})}$$
ここで$Z$は規格化定数である.ポテンシャル関数は狭義に正に限られるため,指数関数で表現すると便利である.
$$ \psi_{C}(\mathbf{x_{\rm{C}}}) = \exp\{-E(\mathbf{x_{\rm{C}}})\} $$
ここで,$E(\mathbf{x_{\rm{C}}})$は__エネルギー関数__(energy function)と呼ばれ,この指数関数表現は__ボルツマン分布__(Boltzman distribution)と呼ばれる.
グラフィカルモデルの重要かつ美しい特徴の1つは,複数の確率変数間の同時分布の__条件付き独立性__を解析的手続きなしに直接グラフから読み取れることである.これを実現する一般的枠組みは__有向分離__(d-separation)と呼ばれる.また同時分布の和を高速に計算して周辺確率を推論するアルゴリズム,同時確率を最大化する確率変数の値の組み合わせを高速に推論するアルゴリズムも知られている(メッセージパッシングによる積和,max-sumアルゴリズム).これらの重要な特徴についてはPRMLを参照.
例:画像のノイズ除去
2値画像のノイズ除去の例を用いて,無向グラフの使い方について説明する.ノイズを含む観測画像が2値ピクセル値$y_{i} \in \{-1, +1\}$の2次元配列として記述されているとする.ここで,$i=1, \dots ,D$はピクセルの通し番号である.この観測画像は,$x_{i} \in \{-1, +1\}$で記述される未知の(ノイズのない)2値画像から,ある小さい確率(ここでは10%)でピクセルの符号をランダムに反転させることによって得られたものとする.
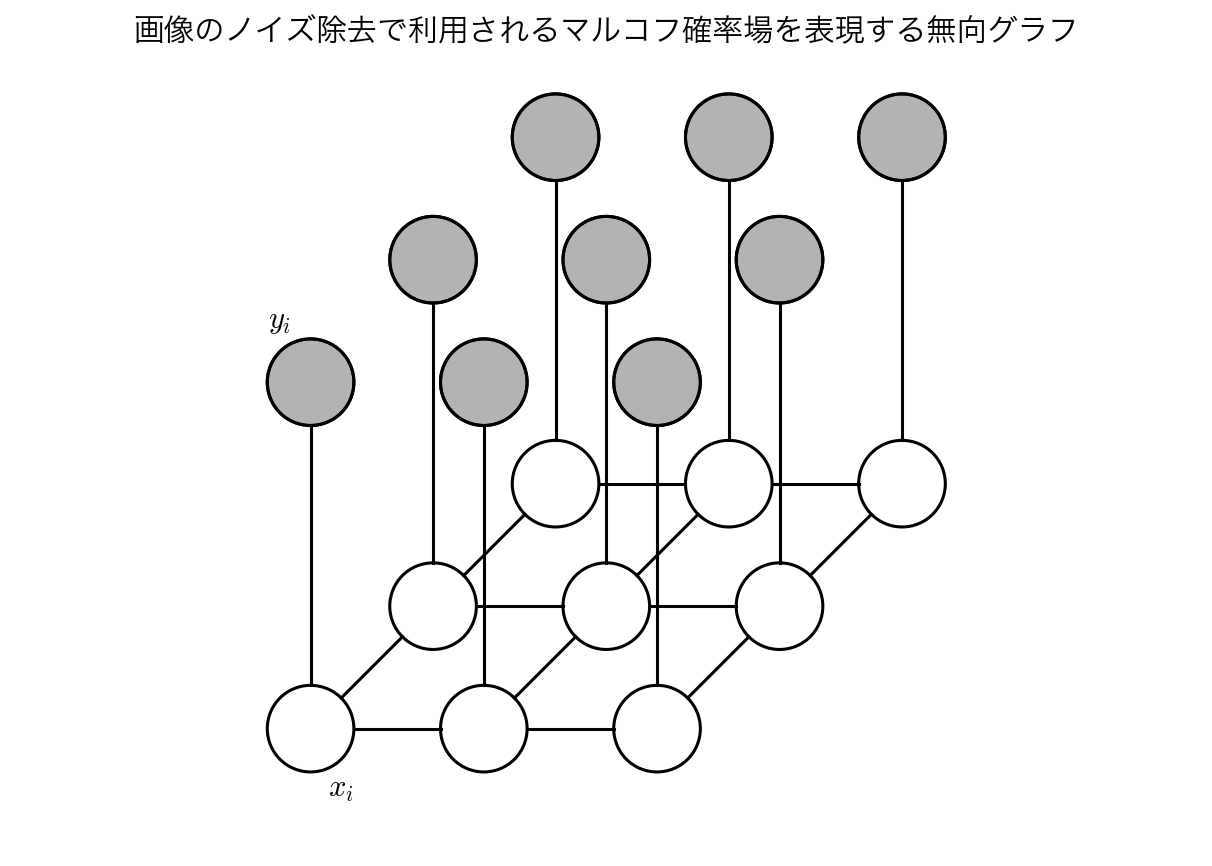
ノイズレベルが十分低いため,$x_{i}$と$y_{i}$の間に強い相関が残っていることが期待される.また,画像中の隣接ピクセル$x_{i}$および$x_{j}$の間にも強い相関があることを知っている.これらの事前知識は,下図に示される無向グラフに対応するマルコフ確率場モデルで表現される.
このグラフは2変数からなるクリークを2種類もつ.$\{x_{i}, y_{i}\}$の形のクリークは,これらの変数間の相関を表現するエネルギー関数に関連づけられる.ここではこれらのクリークに対して,$-\eta x_{i}y_{i}$の形の非常に簡単な関数を用いる.ただし,$\eta$は正定数である.このエネルギー関数は$x_{i}$と$y_{i}$とが同符号のとき低いエネルギー(高い確率)を持ち,異符号のとき高いエネルギー(低い確率)を持つという望み通りの効果を持つ.
もう1種類のクリークは隣接する変数の対$\{x_{i}, x_{j}\}$からなる.ただし,$i$と$j$は隣接するピクセルの番号である.これらのクリークに関しても,2つのピクセル値が異符号の場合よりも同符号の場合の方がエネルギーが低くなるようにしたい.よって$-\beta x_{i}x_{j}$で与えられるエネルギー関数を用いる.ただし,$\beta$も正定数である.
ポテンシャル関数であるためには極大クリーク上の任意の非負関数でありさえすればよいので,クリークの部分集合上の任意の非負関数を掛けることができる.ここではノイズなし画像の$i$番目のピクセル値$x_{i}$の関数として$hx_{i}$という項を追加してもよい.この項は,ピクセル値が特定の符号を持ちやすくなるようにバイアスを掛ける効果を持つ.
以上をまとめると,このモデルの全エネルギー関数は
$$ E(\mathbf{x}, \mathbf{y}) = h \sum_{i} x_{i} - \beta \sum_{\{i, j\}} x_{i}x_{j} - \eta \sum_{i} x_{i}y_{i}$$
と書ける.また,これを用いて,$\mathbf{x}$および$\mathbf{y}$の同時分布は
$$ p(\mathbf{x}, \mathbf{y}) = \frac{1}{Z} \exp\{-E(\mathbf{x}, \mathbf{y})\} $$
で与えられる.$\mathbf{y}$を観測画像に固定すると条件付き分布$p(\mathbf{x}|\mathbf{y})$が決定される.この問題は,統計物理学において広く研究されてきた__イジングモデル__(Ising model)の例である.観測画像$\mathbf{y}$から高い確率を持つ画像$\mathbf{x}$を復元するには,反復条件付きモード(ICM; iterated conditional modes)と呼ばれる簡単な繰り返し法を用いればよい.この方法では単に軸ごとに勾配上昇法が適用されていく.まず始めに変数$\{x_{i}\}$を初期化する.例えばすべての$i$について$x_{i}=y_{i}$とすればよい.次にノード$x_{j}$を1つずつ選んで,その他のノード変数の値を固定したまま$x_{j}$の2つの可能な状態($x_{j}=+1$および$x_{j}=-1$)における全エネルギーを評価する.最後に$x_{j}$の値をエネルギーが小さくなる方に設定する.このような更新を場所を変えて繰り返し,ある適切な停止条件が満たされた時点で終了する.ノードの更新はラスタスキャンで規則的に行ってもよいし,ランダムにノードを選択していってもよい.
下図は,パラメータを$h=0, \beta=1, \eta=1$とした場合の結果である.
考察
- ICMをmax-sumに置き換えた場合も実装したい
- ベイジアンネット,マルコフ確率場,ボルツマン分布に名前負けしていたが,むしろd-分離やメッセージパッシングの方が重要(な気がする)