区間推定
今回は前回に引き続き推定を行っていきたいと思います。
前回は点推定を行いましたので気になる方は見てみてください。
データに関して
今回もPokemonのデータセットを使用して区間推定を行ってみました。
データは下のようになっています。
今回もこのデータのHPのデータをを母集団として区間推定を行っていきたいと思います。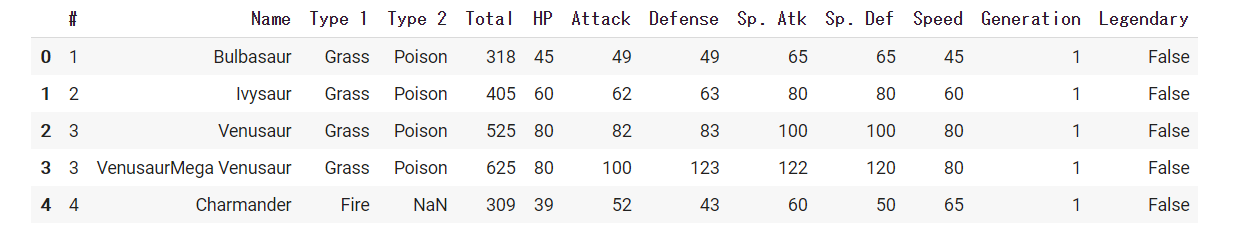
まずHPの平均と分散を求めてみたいと思います。
score = np.array(df['HP'])
mean = np.mean(score)
var = np.var(score)
print("HP 平均: {} , 分散: {} ".format(mean , var))
HP 平均: 69.25875 , 分散: 651.2042984374999
これらを母平均・母分散として分析を行っていきたいと思います。
正規分布の母平均の区間推定(母分散が分かっている場合)
今回先ほどのHPデータを母集団とし、それが正規分布に従っていると仮定したうえでさらに母分散も分かっている場合を考えていきます。
母集団に正規分布を仮定しているため、標本平均$\bar{X}$は$N(μ,σ^2/n)$に従います。
つまり、標本平均という推定量は期待値は母平均μであるものの、標準偏差$\sqrt{σ^2/n}$でばらついている。このような推定量の標準偏差のことを「標準誤差」といいます。
また標本平均$\bar{X}$は$N(μ,σ^2/n)$に従っていることから、$Z = (\bar{X}-μ)/\sqrt{σ^2/n}$と標準化を行うことができ、Zは標準正規分布に従います。この標準化を行うことで何がいいのかというと信頼区間を
計算することが容易に出来るようになるということです。
まず母平均・母分散と標本データの標本平均・標本分散を計算します。
今回の標本のサンプルサイズは20にしています。
np.random.seed(0)
n = 20
sample = np.random.choice(score , n)
p_mean = np.mean(score)
p_var = np.var(score)
s_mean = np.mean(sample)
s_var = np.var(sample , ddof = 1)
母平均: 69.25875 , 母分散: 651.2042984374999
標本平均: 68.8 , 標本分散(不偏分散): 451.26000000000005
今回はこの標本平均を使用して母平均の信頼区間を算出してみたいと思います。(母分散はわかっているとします。)
標本平均から母平均の95%の信頼区間を求めることを考えます。まず標本平均$\bar{X}$を標準化すると$Z = (\bar{X}-μ)/\sqrt{σ^2/n}$となります。そのためまずは$Z$の95%信頼区間を考えてみます。
すると
$P(z_{0.975}≦(\bar{X}-μ)/\sqrt{σ^2/n} ≦z_{0.025})=0.95…①$
という不等式を立てることが出来ます。
この式は確率変数$Z = (\bar{X}-μ)/\sqrt{σ^2/n}$が区間$[z_{0.975},z_{0.025}]$に入る確率が95%であることを表しています。
この$①$の式を母平均のμについての不等式になるように変形すると
$P( \bar{X}-z_{0.025}*\sqrt{σ^2/n}≦μ≦\bar{X}-z_{0.095} * \sqrt{σ^2/n})=0.95$
となります。
よって、母分散が分かっているときの95%の信頼区間を求めるには、
$[\bar{X}-z_{0.025}*\sqrt{σ^2/n} , \bar{X}-z_{0.095} * \sqrt{σ^2/n}]$
を求めればよいということになります。
実装してみました。
rv = stats.norm()
# rv.isf(0.025)には標準正規分布の確率が0.025の点を表している。それに標準誤差を掛ける。
lcl = s_mean - rv.isf(0.025) * np.sqrt(p_var/n)
ucl = s_mean - rv.isf(0.975) * np.sqrt(p_var/n)
lcl , ucl
(57.616, 79.984)
以上より、母平均の95%信頼区間は(57.616, 79.984)であると分かりました。
先程求めた母平均は69.25875でしたので信頼区間内に母平均が含まれていることが分かります。
この信頼区間は同じように何回も標本抽出を行い、区間推定を行うとそのうち95%の区間推定には母平均が含まれるということになります。かみ砕いた形で言ってみると、100回区間推定を行った場合、そのうちの95回は母平均を含む信頼区間が求まるけど、5回は求めた信頼区間に母平均が含まないといったことです。
母分散の区間推定
母分散の区間推定を行っていきます。ここでは母集団に正規分布を仮定し母平均も分かっていない場合を考えてみます。
先程、母平均の信頼区間を算出する際に標準化を行い、標準正規分布に従う確率変数に変換したように、不偏分散$s^2$も何らかの変換を行い代表的な確率分布に従う確率変数を作成する必要があります。
この時に使用される確率分布がカイ二乗分布になります。
不偏分散$s^2$に対して$Y=(n-1)s^2/σ^2$へ変換することでこの変数Yは自由度n-1のカイ二乗分布に従うことが知られています。
では母分散の信頼区間を求めていきたいと思います。まず$\chi{}^2(n-1) $の95%信頼区間を求めていきます。
$P(\chi{}^2_{0.975}(n-1) ≦ (n-1)s^2/σ^2 ≦\chi{}^2_{0.025}(n-1)) = 0.95$
これを今回母分散の信頼区間を求めたいので$σ^2$が真ん中に来るようにします。
$P((n-1)s^2/\chi{}^2_{0.025}(n-1) ≦ σ^2 ≦(n-1)s^2/\chi{}^2_{0.975}(n-1)) = 0.95$
これより、母分散$σ^2$の95%信頼区間は
$[(n-1)s^2/\chi{}^2_{0.025}(n-1) , (n-1)s^2/\chi{}^2_{0.975}(n-1)]$
になります。
rv = stats.chi2(df=n-1)
lcl = (n-1) * s_var / rv.isf(0.025)
hcl = (n-1) * s_var / rv.isf(0.975)
lcl , hcl
(260.984, 962.659)
母分散の信頼区間は(260.984, 962.659)となりました。母分散は651.204であったので区間内に含まれていることが分かります。
母平均の区間推定(母分散が分かっていない場合)
先程母平均の信頼区間を求める際に母分散が分かっているという状況で分析を進めました。しかしながら実際母平均が分からず、母分散が分かっているという状況はあまりありません。
そのため、今回は母分散が分からないときの母平均の信頼区間の推定を行っていきたいと思います。
母分散が分かっているときは、標本平均$\bar{X}$の標準誤差$\sqrt{σ^2/n}$によって区間推定を行いました。今回はこの母分散$σ^2$が分からないため、その代わりに推定量である不偏分散$s^2$を使用した$\sqrt{s^2/n}$を標準誤差として代用します。
まず、母分散が分かっているときと同じように標本平均$\bar{X}$を$\sqrt{s^2/n}$を使用して変換を行います。
$t = (\bar{X} - μ) / \sqrt{s^2/n}$
この$t$は
$Y=(n-1)s^2/σ^2$
$Z = (\bar{X}-μ)/\sqrt{σ^2/n}$
この二つを使用して変換を行うと、
$t = Z / \sqrt{Y/(n-1)}$
で表すことが出来ます。
よってこの$t$は自由度n-1のt分布に従うことが分かります。
今$t = (\bar{X} - μ) / \sqrt{s^2/n}$は自由度n-1のt分布に従うことが分かったので、ここから母平均の95%信頼区間を求めていきます。
$P(t_{0.975}(n-1)≦ (\bar{X} - μ) / \sqrt{s^2/n} ≦ t_{0.025}(n-1)) = 0.95$
この式を母平均のμが真ん中になるように変形します。
$P(\bar{X} - t_{0.025}(n-1) * \sqrt{s^2/n}≦ μ ≦ \bar{X} - t_{0.975}(n-1)*\sqrt{s^2/n}) = 0.95$
これにより、母平均の95%信頼区間は
$[ \bar{X} - t_{0.025}(n-1) * \sqrt{s^2/n} , \bar{X} - t_{0.975}(n-1)*\sqrt{s^2/n} ]$
となります。
rv = stats.t(df=n-1)
lcl = s_mean - rv.isf(0.025) * np.sqrt(s_var/n)
ucl = s_mean - rv.isf(0.975) * np.sqrt(s_var/n)
lcl , ucl
(58.858, 78.742)
母平均の95%信頼区間は(57.616, 79.984)であると分かりました。
先程求めた母平均は69.25875でしたので信頼区間内に母平均が含まれていることが分かります。
まとめ
今回は区間推定を行ってみました。
実際に手を動かして実装を行うことによって理解が深まったりするので手を動かしてアウトプットするのはいいなと記事を書いてて思いました!
<参考資料>
pythonで理解する統計解析の基礎