点推定
点推定に関して簡単に説明していきたいと思います。
まず統計学は大きく「記述統計学」と「推測統計学」の2種類に分けられます。
記述統計学:データを整理し、グラフや表を使用してデータをわかりやすく表すこと。
推測統計学:母集団の一部(標本)を使用して、母集団の情報を推測すること。
今回行う点推定は推測統計学になるわけですが推測統計学の中でも「推定」と「検定」に分かれます。
推定:母集団を特徴づける母数(平均や分散など)を統計学的に推測すること。
検定:母集団から抽出された標本の統計量に関する仮説が正しいかを統計学的に判定すること。
さらに推定には「点推定」と「区間推定」に分けられます。
点推定:平均値や分散などを「1つの値」で推定すること。
区間推定:平均値などを「ある区間」で推定すること。
今回はこの点推定を行ってみます。
データの可視化・準備
今回Pokemonのデータセットを使用して点推定を行ってみました。
データは下のようになっています。
今回はこのデータのHPのデータをを母集団として点推定を行っていきたいと思います。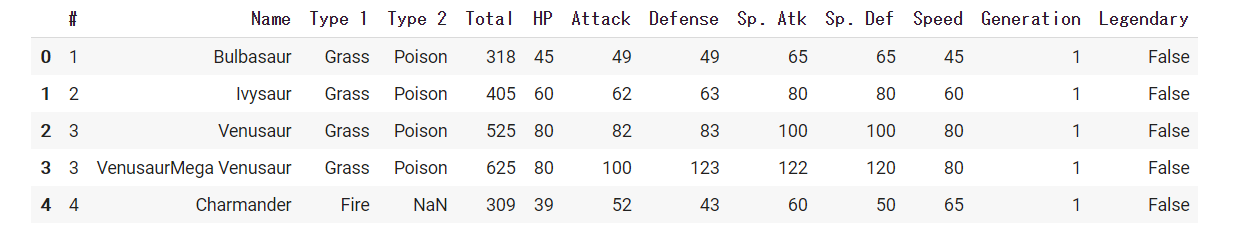
まずHPの平均と分散を求めてみたいと思います。
score = np.array(df['HP'])
mean = np.mean(score)
var = np.var(score)
print("HP 平均: {} , 分散: {} ".format(mean , var))
HP 平均: 69.25875 , 分散: 651.2042984374999
これらを母平均・母分散とします。
今回はこの母集団が正規分布に従っていると仮定して推定を行っていきます。
まずヒストグラムで可視化を行ってみます。
fig = plt.figure(figsize=(10 , 6))
ax = fig.add_subplot(111)
xs = np.arange(300)
rv = stats.norm(mean , np.sqrt(var))
ax.plot(xs , rv.pdf(xs) , color = "gray")
ax.hist(score ,bins = 100 , range =( 0,300) , density=True)
plt.show()
続いて、正規分布に従っているかQQplotを使用して確認してみる。
QQplotは観測値が正規分布に従う場合の期待値をY軸にとり、観測値そのものをX軸にとった確率プロットになります。このプロットの見方としてはプロットが一直線上に並べば、観測値は正規分布に従っていると考えることが出来ます。
stats.probplot(score, dist="norm", plot=plt)
きれいな正規分布とはいきませんが、正規分布に近い特徴を持った分布となっていそうなのでこのまま分析を行っていきます。
標本データを用意します。今回はモンスター20体を標本データとします。
np.random.seed(0)
n = 20
sample = np.random.choice(score , n)
sample
array([ 89, 110, 50, 65, 71, 100, 45, 44, 75, 60, 62, 75, 55,
90, 45, 80, 31, 79, 50, 100])
続いて標本平均の期待値などを求めるためにサンプルサイズ20の標本データを1万組用意しておきます。
np.random.seed(1111)
n_sample = 10000
samples = np.random.choice(score , (n_sample , n))
samples.shape
母平均の点推定
まずサンプルサイズ20のそれぞれの標本平均を見てみます。
for i in range(5):
s_mean = np.mean(samples[i])
print(f'{i+1}回目の標本平均:{s_mean:.3f}')
1回目の標本平均:74.400
2回目の標本平均:70.300
3回目の標本平均:68.850
4回目の標本平均:67.000
5回目の標本平均:75.150
このように標本ごとに平均はバラバラです。
データをそれぞれ見てみるとモンスター20体のHPのデータはすべて同じ期待値μ、分散$σ^2$の確率分布に従います。その標本平均$\bar{X}$の「期待値」は$E(\bar{X}) = μ$となり母平均に一致します。
このように推定量の期待値が推測したい母数になる性質のことを「不偏性」といい、不偏性を持っている推定量のことを「不偏推定量」といいます。
それでは確かめてみます。確かめるために先程作成した20体1万組の標本データの平均をそれぞれ求め、その平均を計算します。
sample_means = np.mean(samples , axis=1) #それぞれの平均を求めている。
np.mean(sample_means)#標本平均の期待値
69.293
母平均の 69.25875と比べてみると、標本平均の期待値は母平均に近くなっていることが確認できます。
他の性質としてサンプルサイズを増やしていくと推測したい母数に収束していくという性質があります。この性質のことを一致性といい、一致性の持っている推定量のことを一致推定量といいます。
では先ほどのサンプルサイズ20を100万にかえて標本平均を見てみます。
np.mean(np.random.choice(score , int(1e6)))
69.273
こちらも母平均の 69.25875と比べてみると、サンプルサイズ100万の標本平均は母平均に近くなっていることが確認できます。
サンプルサイズを増やすことによって標本平均が母平均の値にに収束していくのかを実際にシミュレーションしてみました。
mean_list = [np.mean(np.random.choice(score , i)) for i in range(1 , 100000, 100)]
plt.plot(mean_list)
このようにサンプルサイズを増やすことによって母平均に収束していくことが分かります。
母分散の点推定
続いて母分散の推定を行っていきたいと思います。
まずは平均同様、サンプルのそれぞれの標本分散を見てみます。
for i in range(5):
s_var = np.var(samples[i])
print(f'{i+1}回目の標本分散:{s_var:.3f}')
1回目の標本分散:526.840
2回目の標本分散:585.010
3回目の標本分散:375.028
4回目の標本分散:772.400
5回目の標本分散:537.228
この標本分散が母分散の不偏推定量になっているのかどうかを調べてみます。
作成した1万組の標本データの分散を求め、その平均を計算してみます。
sample_vars = np.var(samples , axis = 1)
np.mean(sample_vars)
620.787
これは母分散651.204と比べると少し小さい値になっています。
では不偏分散を求めるにはどうすればよいのかというと、標本分散における割る数nをn-1にして計算することによって可能になります。不偏分散を$s^2$で表すと、
$s^2 = \frac{1}{n-1}\sum^{n}_{i=1}(X_i-\bar{X})^2$
となります。このn-1は自由度といい、自由に値をとることが出来る変数の数を表しています。
ここで自由度をnからn-1に変えて計算してみます。
自由度をn-1にするときはddof = 1と引数に与えることで可能です。
sample_u_vars = np.var(samples , axis=1 , ddof = 1)
np.mean(sample_u_vars)
653.460
これは母分散651.204と比べると近い値になっています。
また不偏分散は母分散の一致推定量であるかも確認してみたいと思います。サンプルサイズを100万にして確かめてみます。
np.var(np.random.choice(score , int(1e6)) , ddof=1)
653.899
このように分散651.204と近くなっていることが分かり、不偏分散は一致推定量になっていそうです。
まとめ
今回は点推定を行ってみました。
ここでは不偏性や一致性に関してみてみました。
次回は区間推定を行っていきたいと思います。
<参考資料>
点推定とは
pythonで理解する統計解析の基礎


