なんかまた新しい埋め込み手法が提案された。次から次に。
見逃していたけど結構前にbioRxivで提案されていて、すでにUMAPの公式実装に機能が追加されている。
この論文ではt-SNE、UMAPの目的関数に、後述する「ある項」を追加して改良された新手法、Den-SNE、DensMAPを提案。
解決を試みている問題は、t-SNEやUMAPにおいて「高次元空間における密度」の情報が無視されてしまいがちな点。
以下具体的な例で見てみる。
具体例
密度が異なる6クラスタの埋め込み
UMAPの最新バージョンをインストールすると、DensMAPのアルゴリズムを簡単に実行することができる。
import umap
print(umap.__version__)
0.5.0
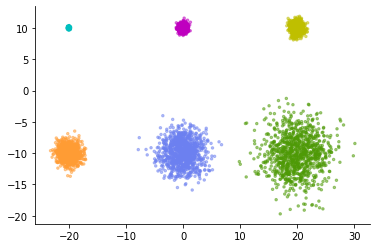
簡単な例として、以下のような6つの正規分布から構成されるデータを考えてみる。
それぞれ1,000個のデータ点からなり、分散に6段階のバリエーションがある。一番小さいクラスタはぎゅっと詰まっていて、一番大きいクラスタはふわっと開いている。
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import make_blobs
X, y = make_blobs(n_samples=6000,
cluster_std=[0.1, 0.4, 0.6, 1.0, 2.0, 3.0],
centers=[(-20, 10), (0, 10), (20, 10),
(-20, -10), (0, -10), (20, -10)],
random_state=42)
colors = ['c', 'm', 'y', '#FF9C34', '#6C80F0', '#4E9A06']
fig, ax = plt.subplots()
ax.scatter(X[:,0], X[:,1], c=[colors[i] for i in y], s=6, alpha=.5)
sns.despine()
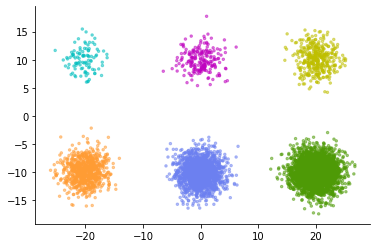
このデータに通常のUMAPを適用してみる。すると以下のような表現が得られる。
normal_model = umap.UMAP(random_state=42)
normal_emb = normal_model.fit_transform(X)
fig, ax = plt.subplots()
ax.scatter(normal_emb[:,0], normal_emb[:,1], c=[colors[i] for i in y], s=6, alpha=.5)
sns.despine()
6つのクラスタがほとんど同じ広がりかたで表現されてしまった。
こういった図を見て、高次元空間では6つの均等な広がり方をしたクラスタがあった、と結論づけてしまうのはありがちな解釈ミス。t-SNEやUMAPではほとんどの場合、低次元可視化されたクラスタの相対的な広がりの差異について議論できない。
しかし、t-SNE結果の解釈に関してそんな感じの警告を再三受けていたとしても、こういった図がミスリーディングであることはまちがいない。直感的な表現ではない。シングルセル解析の論文で図を見たらどうしたって、クラスタの広がりを相対比較したくなってしまう。なんとか高次元空間における広がりをちゃんと反映した低次元可視化が得られないか。
この悩みを(ある程度)解消してくれるのがDensMAP。
使い方は簡単で、通常のUMAPのコンストラクタに densmap=True のパラメータを与えるだけでいい。
densmap_model = umap.UMAP(densmap=True, random_state=42)
densmap_emb = densmap_model.fit_transform(X)
fig, ax = plt.subplots()
ax.scatter(densmap_emb[:,0], densmap_emb[:,1], c=[colors[i] for i in y], s=6, alpha=.5)
sns.despine()
通常のUMAPとは異なる表現が得られた。もともと小さいクラスタはちゃんと小さい広がりで、広がり方の増減を反映してクラスタが表現されている。
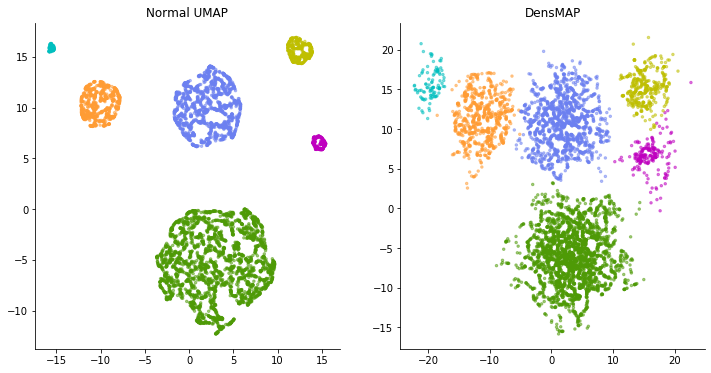
今度は逆のケースを考えてみる。もともとのクラスタの広がりかたは同一だが、それぞれのクラスタに属するデータ点の数が異なる場合。
X, y = make_blobs(n_samples=[100, 200, 400, 800, 1600, 3200],
cluster_std=2.0,
centers=[(-20, 10), (0, 10), (20, 10),
(-20, -10), (0, -10), (20, -10)],
random_state=42)
fig, ax = plt.subplots()
ax.scatter(X[:,0], X[:,1], c=[colors[i] for i in y], s=6, alpha=.5)
sns.despine()
このデータの埋め込みをUMAPとDensMAPで比較してみる。
normal_model = umap.UMAP(random_state=42)
normal_emb = normal_model.fit_transform(X)
densmap_model = umap.UMAP(densmap=True, random_state=42)
densmap_emb = densmap_model.fit_transform(X)
fig = plt.figure(figsize=(12,6))
ax1 = fig.add_subplot(121)
ax1.scatter(normal_emb[:,0], normal_emb[:,1], c=[colors[i] for i in y], s=6, alpha=.5)
ax1.set_title('Normal UMAP')
ax2 = fig.add_subplot(122)
ax2.scatter(densmap_emb[:,0], densmap_emb[:,1], c=[colors[i] for i in y], s=6, alpha=.5)
ax2.set_title('DensMAP')
sns.despine()
今度は逆に、通常のUMAP計算では、もともと同じ広がりであるはずのクラスタが全く異なる広がりかたで表現されてしまった。左の図を見ると、水色のクラスタなどは、いかにも均一なパターンのデータ点で構成された多様性に乏しいクラスタに見えてしまう。しかし実際のところ各クラスタの分散は同一である。単に水色のクラスタはサンプリングされたデータ点の数が少ないだけだ。
一方DensMAPは、完全に、とはいかないけど、クラスタの広がりについてそれほどの差がなく描いてくれている。このようにDensMAPでは実際の密度をある程度反映した表現となる。
論文ではscRNA-seqデータにDensMAPを適用した例がいくつも紹介されている。DensMAPが表現するデータ点の「広がり」は、データから「遺伝子発現パターンの多様性」を解釈する際に有用な情報を提供してくれる。
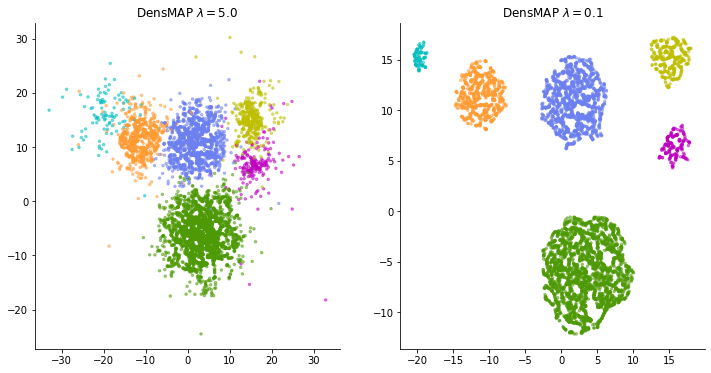
とはいえ、これが唯一正しい表現とは当然言えなくて、実はユーザが調整可能なパラメータがひとつ、追加されている。それは、「密度情報をどの程度重要視するか」を調整するための重みパラメータである。
LASSOとかの正則化項にかかる重みと同じような感じで、この重みパラメータ $\lambda$ を大きくすれば密度をできる限り反映しようとするし、ゼロにすれば通常のUMAPと同じ表現になる。
densmap_model1 = umap.UMAP(densmap=True, dens_lambda=5.0, random_state=42)
densmap_emb1 = densmap_model1.fit_transform(X)
densmap_model2 = umap.UMAP(densmap=True, dens_lambda=0.1, random_state=42)
densmap_emb2 = densmap_model2.fit_transform(X)
fig = plt.figure(figsize=(12,6))
ax1 = fig.add_subplot(121)
ax1.scatter(densmap_emb1[:,0], densmap_emb1[:,1], c=[colors[i] for i in y], s=6, alpha=.5)
ax1.set_title('DensMAP $\lambda=5.0$')
ax2 = fig.add_subplot(122)
ax2.scatter(densmap_emb2[:,0], densmap_emb2[:,1], c=[colors[i] for i in y], s=6, alpha=.5)
ax2.set_title('DensMAP $\lambda=0.1$')
sns.despine()
実データに適用する際、この重みをどのように調整すればいいのかはよくわからない。必ずしも、重みを大きくして密度制約をきつくかければ良い表現が得られるとは限らない。重みを大きくしすぎると今度は、データ点の広がりを重視しすぎてぼんやりと広がったクラスタが多数重なってしまい、t-SNEやUMAPの利点であったはずの「局所構造の表現」がわかりにくくなってしまう。データに合わせてある程度試行錯誤が必要かもしれない。
MNISTの埋め込み
定番のMNIST(手書き数字データセット)でもやってみる。
import numpy as np
dataset = np.load('./mnist.npz')
x = dataset['x_test']
y = dataset['y_test']
x = x.ravel().reshape(-1, 784)
x.shape
(10000, 784)
通常のUMAPの場合。
normal_model = umap.UMAP(random_state=42)
normal_emb = normal_model.fit_transform(x)
import matplotlib
colors = [matplotlib.colors.to_hex(i) for i in matplotlib.cm.tab10.colors]
def plot_clusters(coords, y, ax, labels=None, title=None):
for y_i in np.unique(y):
ax.scatter(coords[y == y_i, 0], coords[y == y_i, 1],
s=6, alpha=0.5, c=colors[y_i])
for y_i in np.unique(y):
centroid = np.mean(coords[y == y_i, :], axis=0)
label = labels[y_i] if labels else str(y_i)
ax.annotate(label, xy=(centroid), fontsize=13, color='white',
bbox={'facecolor':colors[y_i], 'edgecolor':'k', 'alpha':0.8})
if title:
ax.set_title(title)
plt.axis('off')
fig = plt.figure(figsize=(12, 10))
ax = fig.add_subplot(111)
plot_clusters(normal_emb, y, ax, title='MNIST Normal UMAP')
この図はよく見るMNISTの低次元表現。どの数字も同じような広がりのクラスタで構成されているように見える。
一方でDensMAPの場合は、
densmap_model = umap.UMAP(densmap=True, random_state=42)
densmap_emb = densmap_model.fit_transform(x)
fig = plt.figure(figsize=(12, 10))
ax = fig.add_subplot(111)
plot_clusters(densmap_emb, y, ax, title='MNIST DensMAP')
かなり見え方が変わってくる。とくに、「1」の文字で構成されたクラスタ。通常のUMAPではある程度の広がりを持ったクラスタだったが、DensMAPではほとんど直線型のクラスタ構造として表現されている。
実際のところ「1」の文字の描きかたの多様性は、データを見るとほとんどの場合、「直線をどの角度で描くか」の違いでしかない。なので、角度を反映した一次元の構造として表現されるのは妥当っぽい。
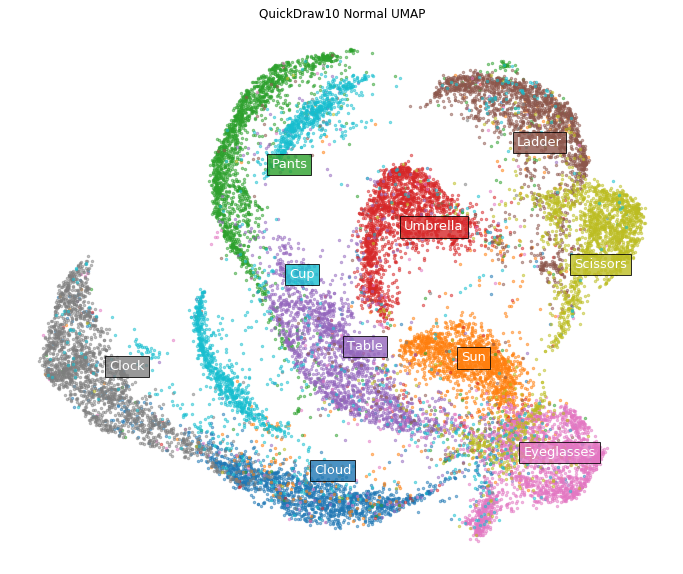
もうひとつ別の例でもやってみる。Googleの落書きデータセット(を10カテゴリにサブサンプリングしたデータ)に同じように適用する。このデータセットは、以下のようにメガネとか傘とかの10カテゴリのお題に対して書かれた絵をMNISTと同じサイズでラスター化したもの。
dataset = np.load('./QuickDraw10-master/dataset/test-ubyte.npz')
x = dataset['a']
y = dataset['b']
x = x.ravel().reshape(-1, 784)
x.shape
(20000, 784)
まずは通常のUMAP。
normal_model = umap.UMAP(random_state=42)
normal_emb = normal_model.fit_transform(x)
labels = ['Cloud', 'Sun', 'Pants', 'Umbrella', 'Table',
'Ladder', 'Eyeglasses', 'Clock', 'Scissors', 'Cup']
fig = plt.figure(figsize=(12, 10))
ax = fig.add_subplot(111)
plot_clusters(normal_emb, y, ax,
labels=labels, title='QuickDraw10 Normal UMAP')
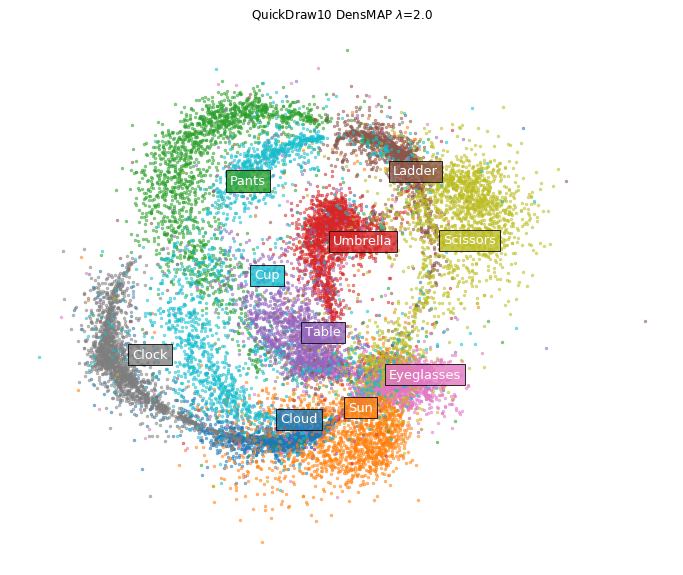
一方DensMAPの場合。
densmap_model = umap.UMAP(densmap=True, random_state=42)
densmap_emb = densmap_model.fit_transform(x)
fig = plt.figure(figsize=(12, 10))
ax = fig.add_subplot(111)
plot_clusters(densmap_emb, y, ax, labels=labels,
title='QuickDraw10 DensMAP $\lambda$=2.0')
メガネ(Eyeglasses)とか雲(cloud)とかのクラスタがキュッと縮まった。たしかにデータの画像を直接見てみると、メガネや雲は描きかたのバリエーションが少なそうではある。
シングルセルRNA-seqデータの埋め込み
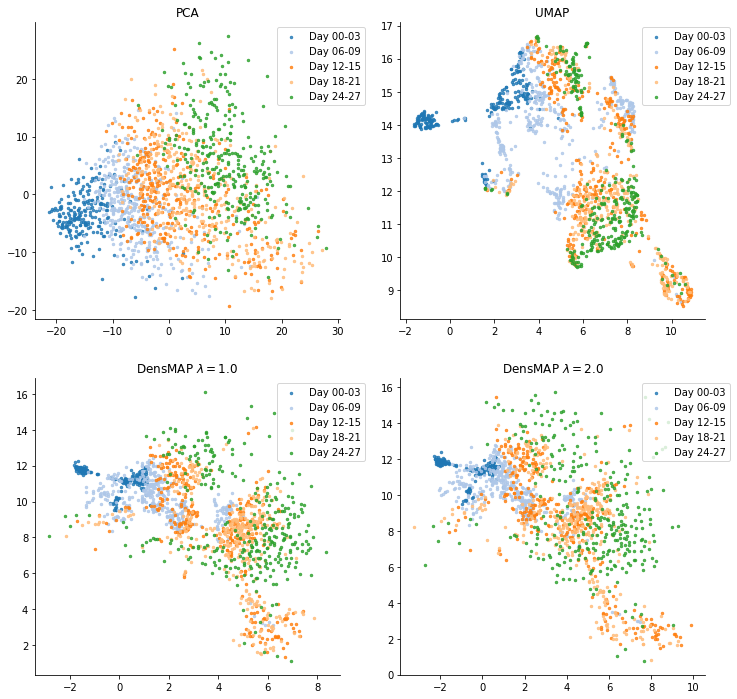
胚葉体分化プロセスのデータ(過去記事参照)にも、いくつかの重みの系列で適用してみた。
重みパラメータ$\lambda$を大きくしていくと、たしかにDay18-21以降の多様性の広がりなどはわかりやすくなる。とくにDay24-27は、通常のUMAPではある程度まとまったクラスタのように見えてしまうが実際は(主成分分析からもわかるように)大きくばらけて分布している。一方、初期の状態(青のクラスタ)は、重みを大きくすることでその密集具合がより強調されていくようだ。
このように通常のUMAPに加え、いくつかの重みパラメータの系列で結果を比較することで、近傍との関係を表現した局所構造だけでなく、データ点周辺密度の相対的な比較も可能となる。
理論
の概要だけ。
t-SNEもUMAPも、各プロセスに使う関数の形が微妙に違うが、やっていることはほとんど同じ。
どちらのアルゴリズムも
- 高次元空間のそれぞれのデータ点について正規分布型のカーネル関数で近傍との距離を確率値に変換する
- 初期状態でランダムに配置された低次元側のそれぞれのデータ点についても近傍との距離を「裾の重い分布」型のカーネルで確率値に変換する
- 高次元側の確率分布と低次元側の確率分布の2つを入力とする目的関数を最小化して、その2つをできるだけ一致させる
問題となるのはひとつめのステップで、正規分布の広がり(分散パラメータ)を決める部分である。t-SNEもUMAPも、固定の幅の正規分布を使うのではなく、データ点ひとつひとつそれぞれについて異なる幅を設定する。つまり、データ点ごとに近傍との距離のスケールが異なる。
なんでこんなことをしているかというと、データの密度が均質ではない場合、固定幅を使うと問題が生じてしまうため。データの中には、データ点が密集して密になっている領域もあれば、他のデータ点との距離が広くスカスカな領域もある。都内の集合住宅みたいに半径10mに何人もご近所さんが住んでる場合もあれば、「ポツンと一軒家」みたいに半径10mに誰もいないこともある。狭い幅に設定して、密な領域のデータ点にとっての近傍を正確に把握できるようにすると、疎なデータ点にとっては「近傍の点」がまったくおらず、他の点との関係性をキャプチャできない。広い幅に設定して、疎なデータ点にとっての近傍を検出できるようにすると、密な領域では幅が広すぎて「近傍の点」が大量に捕捉されてしまい、その中でどれが本当に近かったのかわからなくなってしまう。
これを避けるために、t-SNEやUMAPでは、密な領域では幅を狭く、疎な領域では幅を広く、データ点ごとに幅を適応的に変化させる工夫をしている。これによって、密な領域でも疎な領域でも、どのデータ点にとってもだいたい同じ程度の数の「近傍の点」との距離の大小関係を捕捉できるようになっている。そのようにして捕捉した近傍との距離関係が低次元側でも再現できるようにデータ点を配置すれば、局所構造を維持した低次元表現が得られる。
だがこのプロセスによって、高次元空間における疎密の情報はほとんど失われてしまう。
これを解決するためにDen-SNE、DensMAPが採用しているアイディアはいたってシンプルで、t-SNEやUMAPが最小化する目的関数に、もうひとつ別の項を追加して同時に最小化してしまおう、というもの。
高次元側と低次元側それぞれで、各データ点の周辺密度を計算しておいて、それらのピアソン相関係数を計算し、それに重みパラメータ $-\lambda$ をかけたものを本来の目的関数(t-SNEならカルバックライブラー情報量、UMAPならクロスエントロピー)に加える。それを最小化できれば、データ点ごとの近傍との距離関係の維持と、データ点ごとの局所的な密度の維持、両方がバランスされた表現が得られるはず。
具体的には、高次元側のデータ点ごとの正規分布型カーネル $P$ を、通常通りデータ点ごとの適応的なスケールで計算する。
そして、以下の計算によってデータ点 $x_i$ にとっての周辺のデータ点との「平均距離」$R_p(x_i)$ を、 P で重み付けして計算する。
$R_p(x_i) = \frac {1} {\sum_j P_{ij}} \sum_j P_{ij} ||x_i - x_j||^2$
(このとき「距離」をユークリッド距離ではなく平方ユークリッド距離で測っているけど理由は不明)
この値はデータ点周辺の密度を反映する。密な領域に位置するデータ点では近傍との平均距離は小さく、疎な領域では大きい。
同様に、低次元側のデータ点ごとの「裾の重い分布」型カーネル Q を使って、低次元側の座標 $y_i$ にとっての周辺データ点との「平均距離」 $R_q(y_i)$ を Q で重み付けして計算する。
$R_q(y_i) = \frac {1} {\sum_j Q_{ij}} \sum_j Q_{ij} ||y_i - y_j||^2$
さて、この平均距離を高次元側と低次元側で一致させたいのだけど、それぞれ次元のサイズが異なるので、そのまま一致するわけではなく、$R_q(y_i) \sim \alpha [R_p(x_i)]^\beta$ のようなべき乗則の関係にあると考えられるらしい。
なので、 $r_q(y_i) = log R_q(y_i)$のように両辺対数をとれば、
$r_q(y_i) \sim \beta r_p(x_i) + \alpha$
のように線形な関係となる。
したがって、高次元側と低次元側のデータ点ごとの「平均距離」の一致の良さは、 $r_q(y_i)$ と $r_p(x_i)$ とのピアソン相関係数で測れることになる。
そこで、通常の目的関数にこのピアソン相関係数の値を組み込んでしまえば、Den-SNE、DensMAPの目的関数のできあがりとなる。
t-SNEなら通常の目的関数は P と Q のカルバックライブラー情報量(KL)なので、新しい損失関数が
$\mathcal{L} = KL(P || Q) - \lambda Corr(r_q(y_i), r_p(x_i))$
と設定できて、これを最小化すれば目的が達成できることになる。
また、相関係数の部分に重みパラメータ $\lambda$ がかかっているので、重みを大きくすれば相関を大きくするように配置されていき、重みを小さくすれば相関の値をほとんど無視して通常のt-SNE, UMAPと同じように配置される。
以上、考え方はシンプルだが、微分可能にするための工夫があったり、最適化計算を実行するための勾配の計算はあまりシンプルじゃなかったり、実際はいろいろ複雑なので詳細は論文のSupplementary Noteを参照してください。