はじめに
皆さんこんにちは、「データ構造とアルゴリズムAdvent Calendar」の作成者、文字列大好き文字列初心者の@kgotoです。
一昨年と去年は「文字列アルゴリズムAdvent Calendar」を作り、去年は念願の完走をしました。有り難いことに反響も大きかったです!
今年は「データ構造とアルゴリズム」と対象を広げて、一瞬でカレンダーの枠が埋まるのでは!?とドキドキしていたのですが、蓋を開けてみるとなんとまだ11日も空きがあります!!
ちょっと寂しいですね。。。
もちろん無理に参加してくれとは言いませんが、この記事を読んでちょっとでも面白いと思った方は絶対参加お願いします!
さて、前置きはこれくらいにして本題に入っていきましょう。
データ構造とアルゴリズムAdvent Calendar第1日目では先々月にニュースサイトGigazineにも掲載されて話題になった「ハルヒ問題」を紹介します。
この記事は先月の勉強会で発表したスライドを元に作成しており、興味がある方はそちらも参照していただけるとより理解が深まると思います。
この記事ではスライドで扱っている難しいところはお気持ちだけ話して、問題の面白い性質や話題になった背景などを重点的に話したいなと思います。
ハルヒ問題(Haruhi Problem)
ハルヒ問題とは「最小超置換」と呼ばれる数学(文字列)の問題をアニメ「涼宮ハルヒの憂鬱」に例えて作られた以下の問題です。
$n$話のエピソードからなるTVシリーズについて、全てのエピソードを考えられる全ての順序で連続して視聴するとき、最低限見なければいけない視聴回数を答えよ。但し、各エピソード順序はオーバーラップして良いものとする。
問題文だけ読んでもピンとこないと思うので例で表しましょう。
$n=2$のとき、2つあるエピソードを1, 2と表します。このときこの2話を観る視聴順は12という見方と21という見方の2通りあります。全ての視聴順で観るには1221と合計4話観る方法もありますが、オーバーラップして121と合計3話で観る方法もあります。
$n=3$の場合は、123121321という視聴方法が全ての視聴順を含み最も視聴回数が少なくて済む1つの方法です。
「涼宮ハルヒの憂鬱」は物語の時系列と異なる順に放送するという一風変わったアニメでした。しかし、DVDの収録では各エピソードは時系列順に収録され、どの視聴順で観るのが最適かという議論がアニメファンの間で起こっていたことが、ハルヒ問題が生まれた背景にあります。
つまり全ての視聴順で見ればどれが一番よい視聴順が分かるということですね!
ちなみに現在分かっている最新の成果で、「涼宮ハルヒの憂鬱」第一期14エピソードを全ての視聴順で視聴するには最低でも939億2423万411話視聴する必要があることが分かっています。
最小超置換(Superpermutation)
ハルヒ問題の元になった最小超置換問題の説明に移りましょう。
$n$個の各エピソードにそれぞれ$\{1, 2, ..., n\}$の文字を割り当てその集合を$[n]$と表記すると、視聴順の履歴はアルファベット$[n]$上の文字列として表すことが出来ます。
全てのエピソードを連続で見たということは長さ$n$の文字列の中に$n$個の異なる文字が出現することになり、これは$[n]$の置換となります。
$[n]$の$n!$個の全ての置換を部分文字列として含んだ文字列を$[n]$の超置換と定義し、考えられる全ての$[n]$の超置換の中で最小の長さの超置換を$[n]$の最小超置換と呼びます。
最小超置換問題とは、$n$が与えられたとき$[n]$の最小超置換の長さを求める問題です。
ある性質を満たす数を厳密に求めることは難しいことが多く、そのような場合取り得る解の上界(解が絶対に上回らない数)、下界(解が絶対に下回らない数)を示すのが常套手段です。
つまりハルヒ問題は最小超置換問題の下界を示せという問題ということになります。
さて、文字列アルゴリズム Advent Calendar 2017の読者の中にはここまで読んでピンと来た方もいるかもしれません。
実は最小超置換は上記カレンダーで@okateimにより紹介された最短超文字列問題の入力を制限したサブ問題です。
最短超文字列は文字列集合が与えられたとき、その全ての要素を部分文字列として含む最短の文字列を答える問題です(最短文字列問題は文字列を答え、最小超置換問題は長さを答えるという違いがありますが本質は同じです)。
つまり、最小超置換は入力を$[n]$の$n!$個の置換集合に限定した最短文字列問題と捉えることが出来ます。
最短文字列問題のサブ問題には他にDe Bruijn sequenceなどがあり、これは入力を$[n]$上の長さ$n$の全ての部分文字列に制限した問題です。
面白いことにDe Bruijn問題の場合は解の長さが必ず$n^k + k-1$になることが知られています。
最小超置換のこれまで研究成果
最小超置換が初めて登場したのは[Ashlock and Tillotson, 1993]ですが、彼らはサイズが$\sum_{k=1}^n k!$となる超置換の構築法を示し(つまり上界を示した)、これが最小超置換であると予想しました。
その後反例が見つかり予想が間違っていることが判明しましたが、長年より良い上界、下界は示されてきていませんでした。
2011年の4chanの数学板で「下界を証明した」との匿名の書き込みがありましたが、書いた場所が悪かったのか長年の間研究者の精査を受けずに月日は流れていきました。
大きな進展があったのは、2018年10月にSF小説家Greg Egan氏によって示された新しい上界$n! + (n–1)! + (n–2)! + (n–3)! + n – 3$の証明です。
この進展をきっかけに、4chanの書き込みも精査され下界$n! + (n–1)! + (n–2)! + n – 3$の証明が正しいことが示されました。
証明は研究者らの手によって論文形式に整えられています、第一著者名はAnonymous 4chan Posterです。
- 上記は論文外の出来事で正確な時系列を把握することが難しいですが、Egan氏やその他の研究者らもtwitterでlikeをしている海外のニュースサイトの記述に沿っています。
この記事では[Ashlock and Tillotson, 1993]のシンプルな超置換の構築法、新たな上界、下界の証明の基礎となるPermutation Cityと上界、下界の証明の概要をそれぞれ説明していきたいと思います。
Ashlock and Tillotsonらによる超置換構築法
彼らは長さが$\sum_{k=1}^n k!$となる超置換の再帰的な構築法を提案しました。
$n=1$のとき、アルゴリズムは"1"を出力します、この時の長さは$1!=1$です。
$n>1$のときは次のようなステップを踏んで出力を行います。
例を元に各ステップの動作を確認していきましょう。
$n = 2$のときを考えます。
- $[1]$の超置換を再帰的に計算し、S="1"を得ます。
- "1"に出現する置換を出現順に並べたリスト["1"]を計算します。
- 各要素$y$の後に2を追加したリスト["121"]を計算します
- 要素は1なのでその唯一の要素"121"を出力します、この時の長さは$1!+2!=3$です
"121"は$[2]$の全ての置換["12", "21"]を含んだ超置換で正しく構築できていることがわかります。
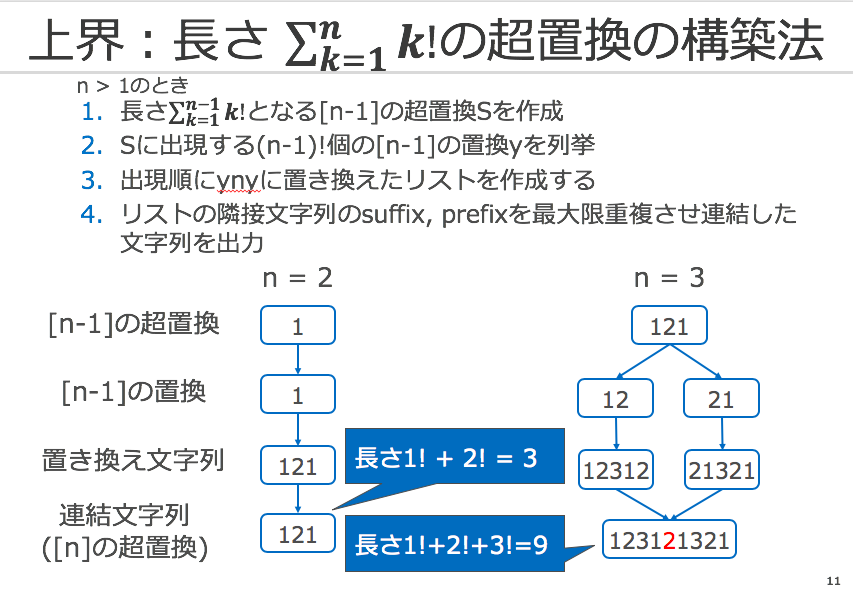
同様に$n=3$のときを考えます。
- $[2]$の超置換を再帰的に計算し、S="121"を得ます。
- "121"に出現する置換を出現順に並べたリスト["12", "21"]を計算します。
- 各要素$y$の後に3を追加したリスト["12312", "21321"]を計算します。
- 各要素を最大限重複させ連結し"123121321"を出力します("2"を重複させました)、この時の長さは$1!+2!+3!=9$です。
"123121321"は$[3]$の全ての置換["123", "231", "312", "213", "132", "321"]を含んだ超置換で正しく構築できていることがわかります。
さて、ポイントは上記の構築法が全ての$n$について正しく超置換が構築できているのかという点と、その長さが$\sum_{k=1}^n k!$になるのかという点です。
前者のアルゴリズムの正当性については以下のよう点で正当性を保証できます。

$yn$となる要素はcyclic-classの代表と考えることが出来ます。
アルゴリズムは全ての$[n-1]$の置換の要素の後に$n$を追加しているため、このような$yn$の置換を全て列挙しています。
また、$yn$のcyclic-classに属する他の要素は$yn$をrotationしたものですが、この置換は$yny$に長さ$n$の部分文字列として必ず出現します。
以上から、アルゴリズムは全ての$[n]$の置換を生成し、それらを連結するため出力文字列は超置換となります。
長さに関する証明は帰納法で証明できます。
大雑把な方針だけを説明します。
アルゴリズムは$[n-1]$の超置換を元に文字を追加して$[n]$の超置換を作成しているのですが、そのときの追加文字数を考えると、ステップ3で各$[n-1]$の$(n-1)!$個の置換の1要素あたり$n$文字追加していることになり、追加文字数は$n(n-1)!=n!$となります。
$n=1$のとき、成り立ちますので全ての$n$についてアルゴリズムの出力が$\sum_{k=1}^n k!$となることが証明できます。
スライドにより詳細な説明を書いていますので興味があれば参照下さい。
Permutation City
最小超置換問題は以下のようにすると巡回セールスマン問題の亜種に帰着できます。
$[n]$の$n!$個の置換1つ1つを都市と見立てます、各都市$x$, $y$について(ここで$x$, $y$は対応する置換)、$x$から$y$へ移動するコストは$x$の末尾に文字を追加してsuffixに$y$が出現する最小の追加文字数とします。
つまり、$x$から$y$への移動は$x$が出現して後に$y$が出現する最小文字列と対応付けることが出来ます。
このとき、全ての都市をセールスマンが最小コストで巡回するとき、そのパスに相当する文字列は最小超置換となり、(細かいところは違いますが)最小超置換問題を巡回セールスマン問題に帰着できます。
新しい上界を示したEgan氏はこのPermutation Cityの考え方をAshlock and Tillotsonらの構築アルゴリズムに適用し、その再帰構造の美しい可視化を示しました。
ちなみに彼の代表作には1994年に出版した「Permutation City(邦題:順列都市)」があるなど、彼とこの問題の関係に運命じみたものを感じてしまいます。
There is another method for touring all the permutations, which has a more orderly recursive structure. But for n > 6, if you’re trying to squeeze all the permutations together into a single string that is as short as possible, it doesn’t do as well as the method described above. pic.twitter.com/vjFr8QIlEr
— Greg Egan (@gregeganSF) 2018年10月22日
Permutation Cityの性質を読み解くと、いくつかいらない都市の移動関係があることに気づきます。
たとえば"123"から"312"へ移動するコストは2ですが、この移動は"123"、"231"、"312"へと3都市間の同じコスト2の移動に分解できるため、不必要なことが分かります。
このような移動を禁止したとすると、以下の性質が成り立ちます。
- ある都市へ到達するコスト1の移動は1つ、ある都市から出ていくコスト1の移動は1つのみ
- ある都市へ到達するコスト2の移動は1つ、ある都市から出ていくコスト2の移動は1つのみ
ある都市$x$から$y$へ移動するとき、コスト$z$で追加する文字種類は$x[1..z]$の文字種類と一致します。
コスト1に関しては末尾に追加する方法は1通りなので自明です。
コスト2に関しては末尾に追加する方法は$2!=2$通りありますが、そのうちの1つは禁止された移動なので上記性質が成り立ちます。
新しい上界、下界の証明はこのPermutation Cityを元に行っています。
Egan氏による上界の証明
難解だったため、詳しい事を理解していませんが、[Williams, 2013]の巡回セールスマン(の亜種)の解法を利用することで$n! + (n–1)! + (n–2)! + (n–3)! + n – 3$の超置換を構築することができるそうです。
Anonymous 4chan Posterらによる下界の証明
コスト1のcyclic-classを全て辿り、その後コスト2で移動して同じくcyclic-classを全て辿る、を続けることによって構成される辿り方を2-loopと呼びます。

全ての2-loopを移動し、全ての都市を移動することを考えます。
このとき、以下の3つの要素を考えると、移動コストが絶対にこの3つの合計以上に、またその3つの合計コストが$n! + (n–1)! + (n–2)! + n – 3$以上になることを示すのが、大雑把な下界の証明の方針です。
- これまで辿った都市の種類数
- 1つ前までに辿ったcyclic-classの種類数
- これまでに辿った2-loopの種類数
こちらも詳細は省きますので興味のある方はスライドを参照下さい。
おわりに
この記事ではハルヒ問題の紹介とその元になった最小超置換問題を紹介しました。
現在でもGoogle Groupsという公開の場で最小超置換問題の議論は活発に行われており、今後も新しい発見や上界、下界の改善が進んでいくことが期待できます。
興味がある方はぜひGroupに参加して議論してみてはどうでしょうか!
長々となりましたが最後まで記事を読んでいただきどうもありがとうございます。