はじめに
この記事では初期化配列の最適な実装方法を説明します(一部の詳細は省略します)。ここで最適とはすべての操作が最悪定数時間で実行でき、かつ必要な領域が通常の配列に加えて定数個の変数に収まることを意味しています。また、本記事では解説しませんが、本記事のアイディアを少し工夫すれば必要な領域を通常の配列+1 bitまで削減することが出来ます。
初期化配列
初期化配列$Z$とは長さ$N$の配列であり、配列の任意の位置の要素の読み込み、書き込み、さらに配列のすべての要素に対して指定した値を書き込む初期化操作、のすべての操作を定数時間で実行可能な配列のことです。
一見、不可能に思われるかもしれませんが、下記記事で解説しているFolklore実装のように、簡単な仕組みで実装することが出来ます。
初期化配列の実装 - Qiita
最適実装はFolklore実装をベースにしているので、まずはFolklore実装の要所をおさらいしましょう。
Folklore実装
Folkloreアルゴリズムでは$F, T, V$の3つの長さ$N$の整数配列と整数$b, \mathit{initv}$を使って以下の管理をしています。Folkloreアルゴリズムの肝は$F$と$T$で作る双方向リンク構造です。
- 初期化後に書き込まれた位置の数を$b$で管理する(同じ位置に複数回書き込んでも1とカウントする)
- $F[i]$が$T[1..b]$のいずれかのポジションと双方向リンクを持つ時、chain、双方向リンクを持たない時unchain、と呼びます。
$Z[i]$が初期化後に書き込まれたか否かをchain/unchain状態で管理します。もし$Z[i]$がchainであれば、$Z[i]$は初期化後に書き込まれており、$V[i]$に保存した書き込み後の値を返します。$Z[i]$がunchainであれば初期値を格納しているはずですので予め保存している初期値$\mathit{initv}$を返します。
初期化に関しては$b=0$に設定するとすべての値をunchainにすることが出来、$Z$の初期化が完了するという仕組みです。
下記がそのFolklore実装のレイアウトになります。
以上のようなしくみで読み込み、書き込み、初期化のすべての操作を定数時間で実現しています。(書き込みの操作については省略します)
最適実装
Folklore実装をベースとして、長さ$N$の整数配列$A$と$b, \mathit{initv}$のみで初期化配列を実現する方法を解説します。アイディアは単純です。$F, T, V$の3つの配列を1つの配列$A$に詰め込みます。
まずは、$A$のレイアウトと$Z[i]$の読み込み方法だけに着目してみましょう。
レイアウト
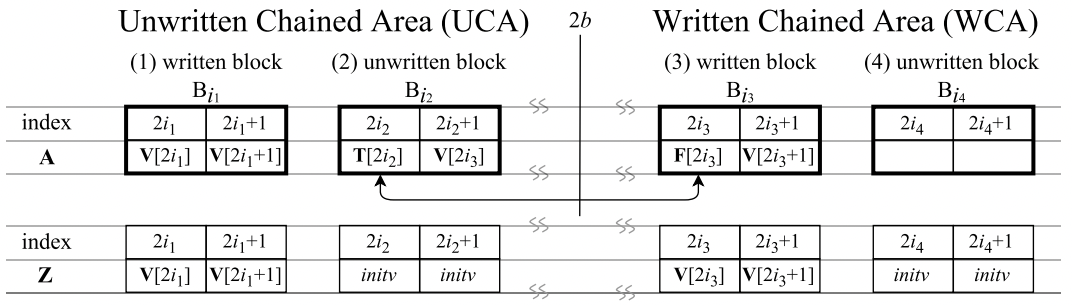
レイアウトは以下の図のようになります。
レイアウトの要点
- chainを1要素単位でなく、2要素単位のブロック単位で管理します
- $2b$をしきい値として、$2b$未満と、$2b$以上に領域を分けます、左、右の領域をそれぞれUCA、WCAと呼びます
- chainの定義をUCAブロックの先頭要素とWCAの先頭要素が双方向リンクを持つ、と変更します。
読み込み方法
それではこのレイアウトの上で$Z[i]$の読み込みを読み込みをどう行うかについて説明します。
$Z[i]$が所属するブロックの値の読み込みを考えることにしましょう。
各ブロックはUCAとWCAのどちらに所属するか、chainを持つか、の4状態持ちます。
この各状態に応じてブロックの値の読み込み方法が以下のように異なります(レイアウトの図と対応付けて読んでください)。
- $B_{i_1}=(Z[2i_1], Z[2i_1+1])$ is unchain block in UCA: $(A[2i_1], A[2i_1+1])$
- $B_{i_2}=(Z[2i_2], Z[2i_2+1])$ is chain block in UCA: $(\mathit{initv}, \mathit{initv})$
- $B_{i_3}=(Z[2i_3], Z[2i_3+1])$ is chain block in WCA: $(A[2i_2+1], A[2i_3+1])$
- ここでブロック$B_{i_3}$と$B_{i_2}$はchainしているブロック
- $B_{i_4}=(Z[2i_4], Z[2i_4+1])$ is unchain block in WCA: $(\mathit{initv}, \mathit{initv})$
つまり1つの配列をUCAとWCAの2つに分けて、$F, T$の関係を1つの配列で表現しています。UCA側はchainブロック$B_{i_2}$がFolkloreと同じように初期値を返し、反対にWCA側はunchainブロック$B_{i_4}$が初期値を返します。UCA側のunchainブロックは$B_{i_1}$はFolkloreと同様に$A$の同じ位置に保存された書き込み後の値を返します。問題はWCAのchainブロック$B_{i_3}$です。このブロックはchainしているため、先頭要素$A[i_3]$はそのリンクのために使用しており、$B_{i_1}$のように書き込み後の値を$A[{i_3}]$に保存することは出来ません。ではどうするかというと、リンク先の$A[2i_2+1]$が未使用なので、このスペースに書き込み後の値を保存します。
上記説明から分かる通り、定数時間で任意の要素$Z[i]$を読み込むことが出来ます。
その他操作
初期化操作は$b=0$とすればすべてブロック$B_{i_4}$の状態になり初期化が完了し、初期化に関しても定数時間で実行できます。
書き込み操作は、ある値を書き込むときに、書き込み前のレイアウトから書き込み後のレイアウトに定数時間で変更する操作、とみなすことが出来ます。実現は難しくはないですが、すこしややこしいですので説明を省略することにします。書き込み操作についても定数時間で実行できます。書き込み操作の実現はパズルのようなものですので、興味がある方はぜひご自身でぜひ考えてみてください。
おわりに
以上より初期化配列$Z$を1つの整数配列$A$と2つの整数$b$と$\mathit{initv}$で実装することが出来ました。
$b$と$\mathit{initv}$の領域を1 bitにすることも出来ます。これもパズルのようなものなのでぜひ考えてみてください。