初期化配列の実装

こんにちは、最近ハマっている初期化配列について紹介したいと思います。

はじめに

皆さんプログラミングをする時に配列を使ってますか？使ってない人はほとんどいないのではないでしょうか？
長さNの固定長配列AはN個の要素を格納でき、かつ任意の位置に保存された要素A[i]を最悪定数時間（以下、定数時間）で読み書き可能な最も基本的なデータ構造の一つです。配列の様々な操作の中で読み書きについで頻出する重要な操作が、配列の全ての要素を指定した値に書き換える初期化操作です。配列の初期化は配列長に対して線形な時間がかかるため、配列長が長い場合や、初期化が頻出する処理では配列の初期化操作が大きなボトルネックとなります。この問題を解決するデータ構造が初期化配列です。本記事ではシンプルな初期化配列の実装法、folkloreアルゴリズムを紹介したいと思います。

初期化配列

初期化配列とは通常の読み書きに加え、配列の全ての要素を任意の値に設定する配列の初期化も定数時間で行うことが可能な特別な配列です。そんな事が本当に出来るのかという感想を抱くかもしれませんがそれが出来るんです。もちろん本当に全ての要素への書き込みを定数時間で行うことは出来ません。ただし、まるで全ての要素を書き込んだかのように振る舞うことは出来るんです。

Folkloreアルゴリズム

初期化配列の実装方法については実は昔から知らています。真の作者は不明ですが、1974年Ahoらの書籍¹によって始めて初期化配列の存在について言及され、その後Mehlhorn²、Bentleyらの書籍³で具体的な実装方法が示されました。今回はBentleyの書籍で説明されたアルゴリズムをFolklore（伝承）アルゴリズムとして説明したいと思います。

Folkloreアルゴリズムでは3つの長さNの配列V, F, T（Value, From, Toの頭文字）と２つの変数b, initvで初期化配列Zを実装します。Zは抽象的な配列で実体はありませんが、補助データ構造（V, F, T, b, initv）を使ってまるでZが存在するかのように振る舞います。ここでinitvは初期値を保存し、Tはstack、bはTのスタックサイズを表します。
これらを使って次の不変条件を維持します。

• V[i]がchainを持つならばZ[i] = V[i]
• V[i]がchainを持たないならばZ[i] = initv

ここでchainとはF[i] = j < b, T[j] = iとなり、お互いにリンクを持つ状態のことを言います。
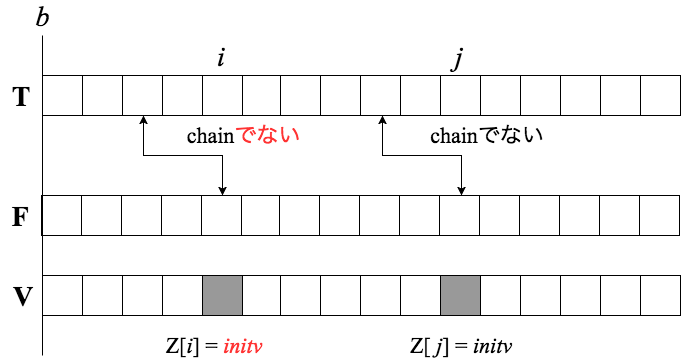
下記の図（簡単のため全てのchainは表示してません）ではV[i]がchainを持つのでZ[i]=V[i]、V[j]はF[j]とT[F[j]]=jと相互リンクがありますがF[j] ≧ bのためchainではなく、Z[j]=initvとなります。

さてこの不変条件から読み書き、配列の初期化は以下のように導けます。全て定数回の操作で完了します。

• Z[i]の読み込み：V[i]がchainを持つかチェック、chainがあればV[i]を返し、chainが無ければ初期値initvを返します。
• Z[i] ← vの書き込み：V[i]がchainを持つならばV[i]に書き込み、持たないならばbを1増加させ、空いたスペースを使ってV[i]にchainを作り、書き込みます。b ← b + 1、F[i] ← b-1、T[b-1] ← i、V[i] ← v。
• Z[i] ← v for all iの初期化：不変条件から全てのchainを削除すれば初期化が完了したことになります。initv ← v、b ← 0とし、全てのchainを削除すれば完了です（下記の図を参照）。

おわりに

如何でしたか、一見不可能に見える配列の定数時間の初期化が驚くほど簡単に実装可能なことを実感出来たでしょうか。初期化配列は普通の配列よりも高機能ですが幾つかの課題があります。

• 読み書きが普通の配列に比べ遅い：配列のランダムアクセスが複数回必要でキャッシュミスが起こりやすいため、どうしても時間がかかってしまいます。
• 普通の配列の３倍以上の領域が必要：究極的には時間はそのままで領域が定数領域の実装が求められています。

実は２つ目の課題については既に解決されています。Katoh and Gotoの論文⁴では普通の配列の領域にたった1 bitの追加領域を加えただけで初期化配列を実現しています。実装はfolkloreアルゴリズムのシンプルな拡張で、folkloreアルゴリズムと同様にV, F, T, b, initvを使います。但しそれら全ての補助データ構造を単一の長さNの配列に埋め込むことで、追加1 bitでの初期化配列の実現に成功しています。とてもシンプルな実装ですので興味があればぜひ読んで見て下さい。そして、ぜひ一つ目の課題である実用に高速な実装についてぜひ取り組んでみて下さい。

P.S. 競技プログラミングで初期化配列がときどき使われていると、ちらっと耳にしたのですが本当でしょうか？
どんな場面で使われているのか興味があるので、ご存知の方は問題のリンクなど教えて頂けるととてもうれしいです。

1. Alfred V. Aho, John E. Hopcroft, and Jeffrey D. Ullman. The Design and Analysis of Computer Algorithms. Addison-Wesley, 1974. ↩

2. Kurt Mehlhorn. Data Structures and Algorithms 1: Sorting and Searching, volume 1 of EATCS Monographs on Theoretical Computer Science. Springer, 1984. ↩

3. Jon Louis Bentley. Programming pearls. Addison-Wesley, 1986. ↩

4. Takashi Katoh, Keisuke Goto, In-Place Initializable Arrays. CoRR abs/1709.08900, 2017. ↩