これはAmusementCreators AdventCalendar2018の25日目の記事です。
AmusementCreatorsのkerochanです。今回は、前回の記事(システムと状態方程式)の続きとしてシステムの制御のための最も基本的な方法である、状態フィードバックについて話します。
はじめに
この記事は前回の記事の続きなので、前回の記事を読まないとなんのこっちゃな部分が出てくると思います。そのため、前回の記事を読むことをお勧めします。
さて、前回の記事ではシステムを状態方程式を用いて記述し、その安定性について説明しました。また、可制御性と可観測性という概念についても説明し、それと安定性との関連も同時に示しました。
今回の記事ではその可制御性と可観測性に関連した事項でありかつ制御の最も基本的な方法でもある状態フィードバックについて説明します。
状態フィードバックと可制御性
状態フィードバック
過去の記事でも説明したのですが、システムが安定して動作するためには制御することは不可欠です。制御なしでは、どんどん速度の増加する自動車や飛行中常に上下に振動する飛行機などが作られてしまう可能性があります。このような不安定な状態を解消するために制御は必要不可欠であることはわかると思います。
その制御を実現させるための方法の1つに状態フィードバックがあります。これは、簡潔に言えば状態変数を入力として利用する、という制御方法です。この方法は、伝達関数の表現でのフィードバック制御と似た方法です。フィードバック制御が最も基本的な制御方法であることがうかがえると思います。ただし、状態フィードバックを行うためにはある条件が必要となりますがこれは次項で詳しく説明します。
状態フィードバック制御を施したシステムの状態変数線図は下図のようになります。ただし、${\bf b}$はn次のベクトルであるとします。
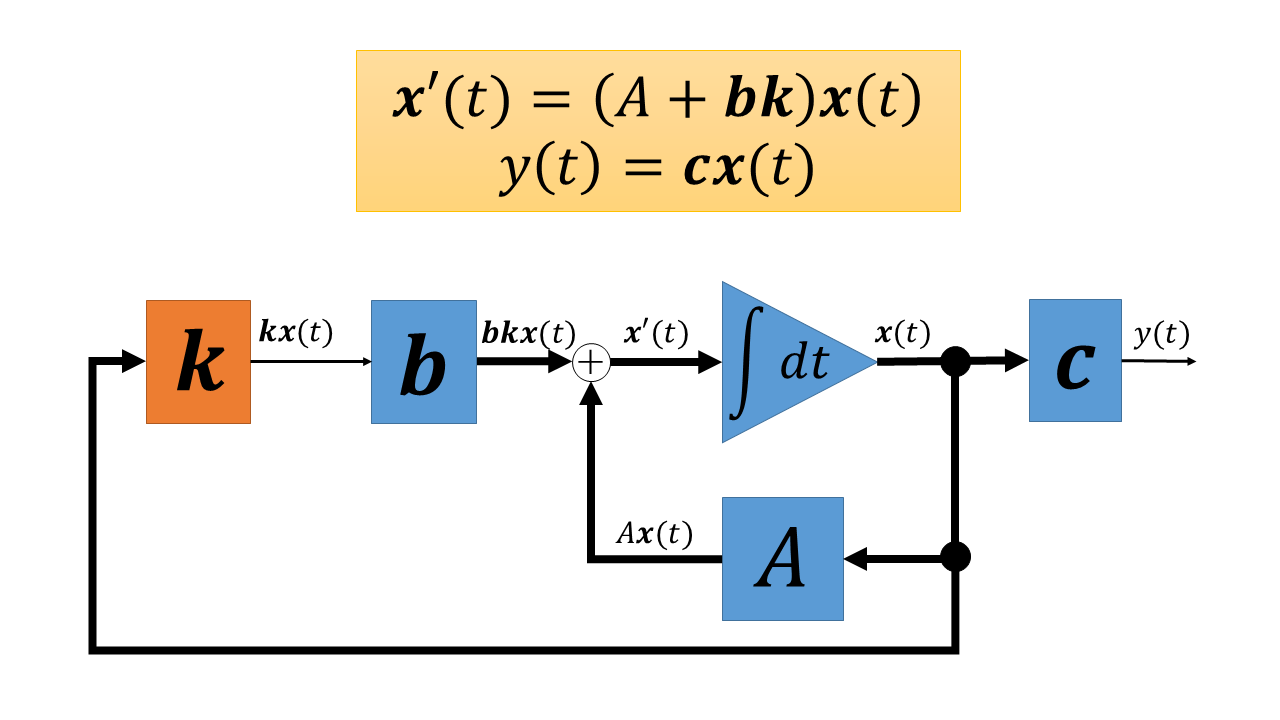
上図を見ると、確かに状態変数が入力に用いられいます。上図において${\bf k}$をフィードバックゲインと言い、なお、フィードバックゲインは行ベクトルで、${\bf k} = (k_1, k_2, \cdots, k_n)$です。PID制御における比例器のような見た目をしています。このフィードバックゲインの値によってシステムの安定性が大きく変化します。
上図の数式を見るとフィードバックゲインをかけたシステム全体のシステム行列が$A + {\bf bk}$(${bk}$はn*nの行列になります)となり、フィードバックゲインがシステム行列に影響していることがわかります。このことはすなわち、フィードバックゲインの値によってシステム行列の固有値が変化することと同じです。前回の記事で、システムの安定性はシステム行列の固有値の実部によって決まると書きましたが、このことから固有値が変化すればシステムの安定性も変化することがわかります。つまり、このフィードバックゲインの値によってシステムの安定性が大きく変化する理由は、フィードバックゲインの値がシステム行列の固有値を変化させるからです。
このフィードバックゲインは制御システムの設計者が自由に決められるため、必ずシステムを安定させることができるということがわかります。
状態フィードバックが可能な条件
前項の初めに、フィードバック制御が可能な(正確には意味をなす)条件がある、と書きましたがこの条件がまさに可制御であるということです。その理由は、入力がシステムに影響しないということは、そもそも状態変数を入力として利用することで制御を行うフィードバック制御はそもそも意味をなさないからです。
もう少し詳しく説明します。前項で示した図のシステム行列$A - {\bf bk}$(この行列の変換を$\tilde{A_k}$とします)の${\bf bk}$に注目してみます。ただし、${\bf b} = (b_1, b_2, \cdots , b_n)$の列ベクトルとします。
実は対角正準計形式へ変換する際、$A - {\bf bk}$の変換途中で${\bf \tilde{b}}$を含む項($A$と行、列の数が同じ行列)が出てきます。もしもシステムが可制御でない場合、その行列に0だけが並ぶ行ができます。最終的にはこの行列と元のシステムの行列$A$との和が$\tilde{A_k}$となるため、可制御でないということはフィードバック制御前のシステム行列の固有値がフィードバック制御後もそのまま現れる、すなわち制御が意味を成さないモードが存在するということになります(あくまでも意味をなさないだけで、フィードバック制御自体は可能)。
このことを図で表すと下図のようになります。
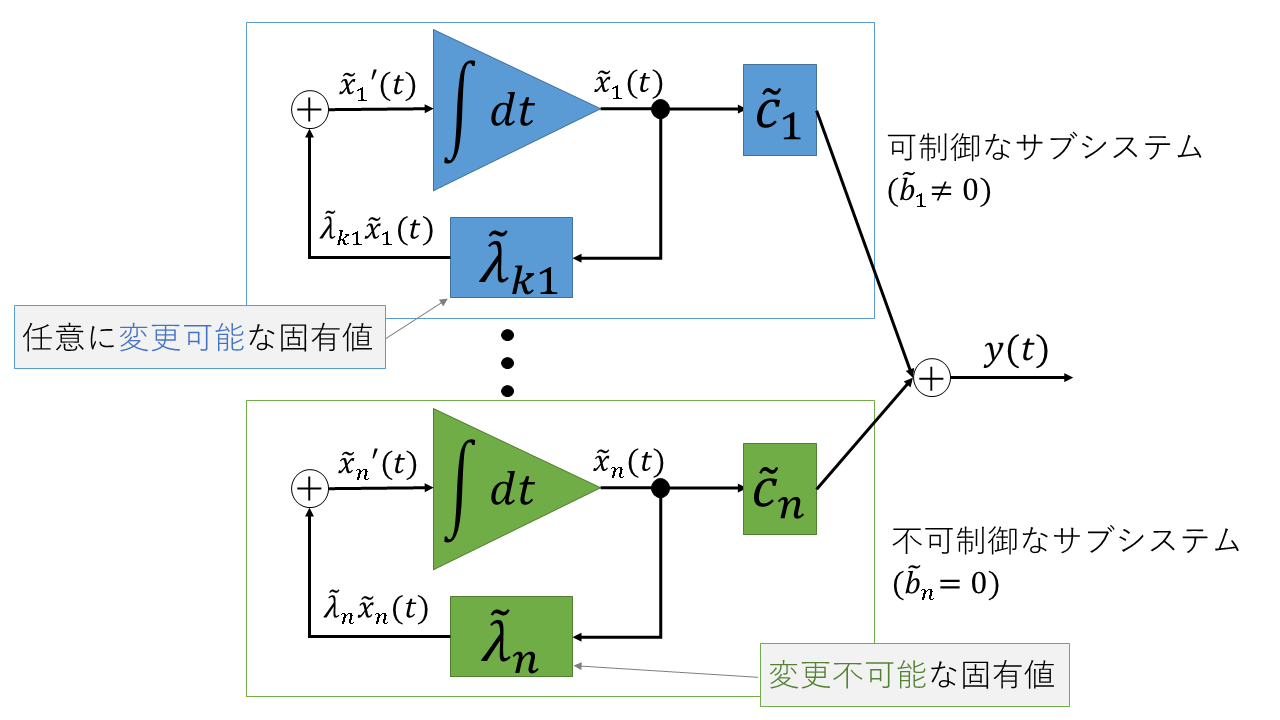
まとめると、フィードバック制御が意味を成す条件はシステムが可制御であるということが言えます。
まとめ
この記事では、状態フィードバック制御について説明してきました。まとめとして、次の2つを書いておきます。
- 状態変数を入力として利用する、状態フィードバック制御によってシステムの安定性を変化させられる
- 状態フィードバック制御は、システムが可制御でないと意味をなさない