これはAmusementCreators AdventCalendar2018の24日目の記事です。
AmusementCreatorsのkerochanです。今回は、前回までの記事でシステムを伝達関数で表現しました。今回の記事では、システムを状態方程式という別の表現方法を用いて表現した時の安定性などを考察していきます。
はじめに
前回までのAdventCalendarの記事ではシステムを伝達関数という形を用いて表現することでシステムの安定性などを考えていました。この伝達関数とは別に、もう1つシステムの表現方法がありこれを状態空間表現といいます。
状態空間表現ではモデルをベクトルを用いた方程式の形で表現されます。そのため、この表現方法を用いるには線形代数、特に行列と固有値に関する知識が必要となりますが、それらに関する具体的な内容はあまり書かないようにして、こういう風な方法でやればできるよという程度の表現にとどめておこうかと思います。
なお、伝達関数と状態空間表現はモデルの表し方が異なるだけで、この表現での目的は、システムの安定性の判別やフィードバック制御など伝達関数で表現した場合と同じです(ただし各表現方法で適用される理論は異なります)。イメージとしては下図のような感じです。
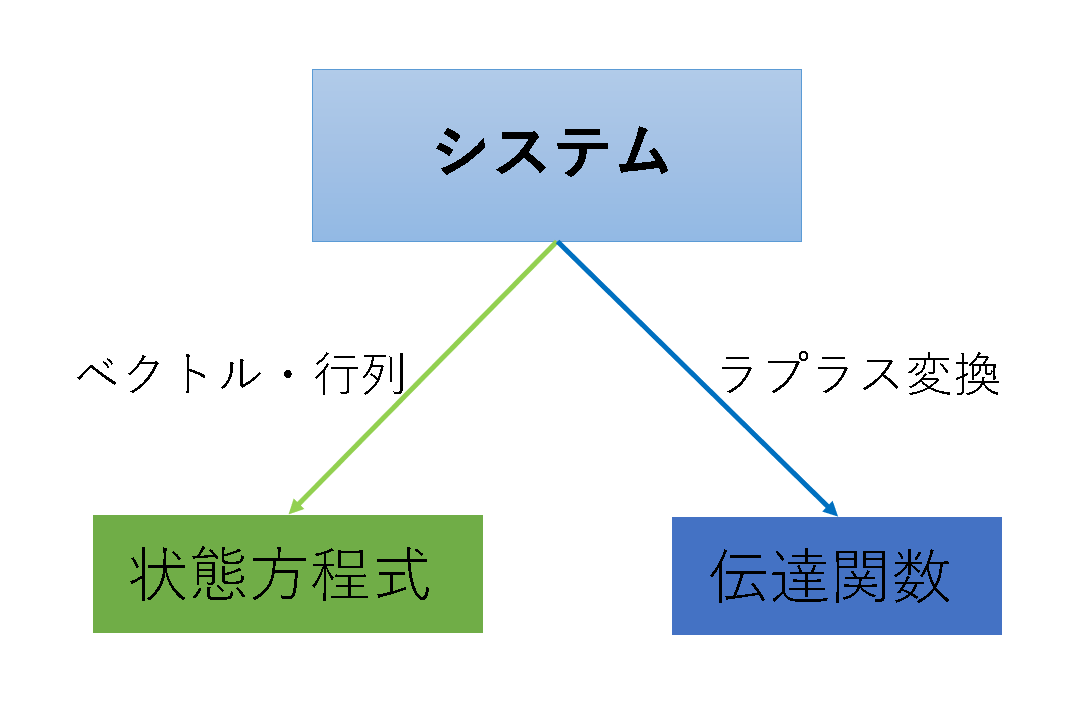
状態方程式
この記事では線形時不変システムを考えるので、システムのモデルは次の式で表されます。
\sum_{i=1}^n a_i \frac{d^i x(t)}{dt^i} = \sum_{i=1}^m b_i \frac{d^i u(t)}{dt^i}
この式を見ると、このシステムは入力に関して$n$階の線形微分方程式となっていることがわかります。
今からこれを1階の線形微分方程式として書き直してみましょう。
そのための道具としてベクトルと行列を使います。この2つを用いて、まず入力$u(t)$を下式のようなベクトルとして表します。これを入力ベクトルといいます。なお、${}^t$は転置を表しています(ベクトルには列ベクトルと行ベクトルがありますが、この違いは重要です)。
{\bf u(t)} = {}^t(u(t), u'(t), \cdots , u^{(m)}(t))
ここで、新たに状態変数ベクトルというものを導入します。これはシステムの内部の状態を表すベクトルで、これがそのまま出力を表すこともあればそうでない場合もあります。状態変数ベクトルは、要素の数が出力と同じで次のような形をしています。
{\bf x(t)} = {}^t(x(t), x'(t), \cdots , x^{(n)}(t))
今回は状態変数ベクトルが出力を表していますが、例えば連立線形微分方程式などでは出力と状態変数ベクトルは異なることが多いです。そのような場合、入力と出力はまた別の方程式を用いて表されますが、これについては後程すぐに出てきます。
さて、入力ベクトルと状態変数ベクトルを用いれば、上のモデルは下のように表されます。ただし、$A$はn行n列、$B$はn行m列の行列です。
{\bf x(t)}' = A{\bf x(t)} + B{\bf u(t)} \\
A = \left[
\begin{array}{rrrrr}
0 & 1 & 0 & \ldots & 0 \\
0 & 0 & 1 & \ldots & 0 \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
0 & 0 & 0 & \ldots & 1 \\
-a_1 & -a_2 & -a_3 & \ldots & -a_n
\end{array}
\right]
\
B = \left[
\begin{array}{rrrrr}
b_1 & 0 & 0 & \ldots & 0 \\
0 & b_2 & 0 & \ldots & 0 \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
0 & 0 & 0 & \ldots & b_m \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
0 & 0 & 0 & \ldots & 0
\end{array}
\right]
これを状態方程式といいます。また、行列$A$をシステム行列、$B$を入力係数行列といいます。また、${\bf x(t)}'$はベクトルの各要素を微分したベクトルです。この方程式でシステム行列$A$はシステムの安定性にとって特に重要なのですが、これについては後述します。このように、n階の微分方程式でもベクトルと行列を用いることで、ベクトルとしては1階の線形微分方程式に書き直すことができます。そのため、この方程式の解を求める場合1階の線形微分方程式の解き方を応用でき、非常に便利な書き表し方になっています。この記事では、この状態方程式を用いてシステムの安定性などを考えていきます。
出力方程式
状態方程式による表現は、伝達関数による表現よりも優れた部分がいくつかありその1つが任意の状態変数を参照できるという点です。
伝達関数の場合は例えば出力が変位の場合、出力である変位は即座に確認することはできますが、速度や加速度も同時に確認することは困難です(もちろんできないわけではなく、微分を用いることで求めることはできます)。しかし、上の状態方程式ではx(t)のn階微分も同時に計算できていることがわかります。つまり、状態空間表現では複数の出力を同時に計測できるということです。
いま、状態変数ベクトルの要素のうち$x(t)$を出力$y(t)$として知りたいとします。このとき、出力と状態変数ベクトルの関係を下の式のようにすれば、$x(t)$の値が求められることはすぐにわかると思います。
y(t) = {\bf c}{\bf {}^tx(t)} \\
{\bf c} = (1, 0, \cdots , 0)
上式を出力方程式といいます。また、${\bf c}$を出力変数ベクトルといい、出力としたい値をこのベクトルが選択していることがわかります(厳密にはこの言い方は正しくはない)。
このように状態空間表現の強みは、「複数の出力を同時に計測できる」ことと「任意の状態変数を選択できる」ことで、これにより伝達関数よりも多くの出力(状態変数)を用いてシステムの特性などを検討することができるようになります。
システムの安定性
これまで、何の定義もなく「安定」という単語を用いてきました。「安定」と一口に言っても解析対象や方法によって複数の定義があります。もちろん状態空間表現でも定義が複数存在するのですが、この記事では次の定義を用いることにします。
「システムに有界な入力を与えると必ず有界な出力が得られる」
これを、システムはBIBO安定である、といいます。(ちなみに、BIBOはboundary input boundary outputの略です)
つまり、安定性というのはシステムがBIBO安定かどうかということを意味しています。
では、システムが安定かどうかを判別するにはどうすればよいでしょうか。
まずは上で示した状態方程式を解いてみるのがよいでしょう。こうすることで、状態変数の具体的な形がわかるため安定性の判別が容易になります。
これから早速この方程式を解いていきますが、その前に1つ重要な図を紹介します。これがあると、後に状態方程式を変形したのちに、なぜ安定なのかということが理解しやすくなります。
状態変数線図
状態変数線図は、状態変数の流れを表した図です。この図があると、状態変数の流れを直感的に把握できるので非常に便利です。この図は、ベクトルは矢印で書くことや、積分は四角ではなく三角で表すなど細かな違いはあれど、ほぼブロック線図と同じです。ブロック線図についての説明は前回の記事にごく簡単にですが書いてあるのでそれを参考にしてください。
例として、初めに示した状態方程式と出力方程式を状態変数線図として表すと下図のようになります。ただし、${\bf x(t), u(t)}$は列ベクトルであるとします。
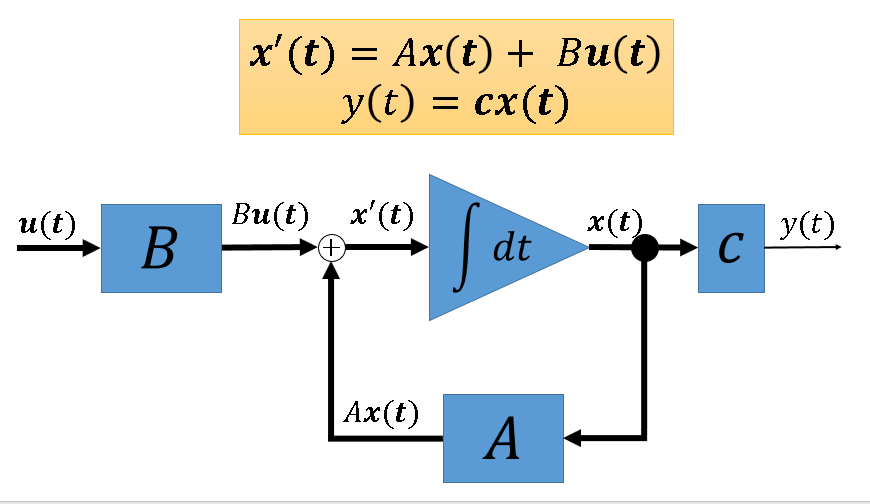
行列の対角化と対角正準形式
図の紹介が終わったところで、さっそく状態方程式を解いていきましょう。この記事では簡単のため、入力は$u(t)$のみであるとします。よって、入力係数行列はベクトルとなり入力ベクトルはスカラーとなります。また、状態変数ベクトルは列ベクトル、出力係数ベクトルは列ベクトルであるとします。このとき状態方程式と出力方程式は下式のようになります。
{\bf x'(t)} = A{\bf x(t)} + {\bf b}u(t) \\
y(t) = {\bf cx(t)}
状態方程式を解くとは言っても、このままでは解くことが難しいのでシステム行列$A$に対角化という操作を施して対角正準形式という形式に状態方程式を変換します。この形式は、システム行列が対角行列に変換された形式で状態変数の具体的な形を求めることが簡単で、しかもベクトルによる方程式をスカラーの方程式の組で表すことができるため、なぜ安定かどうかを理解しやすいという利点があります。
対角正準形式に変換できる条件は、システム行列の固有値の実部が0でないかつ同じものが存在しないというものです。固有値というのは、システム行列の固有方程式(n次方程式)の解のことで、この固有値というのがシステムの安定性に大きく関わっています。なお、固有値は複素数になります。
もし対角正準形式に変換できれば、変換されたシステム行列の対角の成分(行列の要素を成分と言います)に固有値が並びます。
システム行列$A$の固有値を$(\lambda_1 , \lambda_2, \cdots, \lambda_n)$とすれば、変換後の状態方程式と出力方程式は下式のように表されます。なお、$\tilde{}$の付くベクトルや行列は元のベクトルや行列と対応しており、変換されたということを示しています。
{\bf \tilde{x}'(t)} = \tilde{A} {\bf \tilde{x}(t)} + {\bf \tilde{b}}u(t) \\
y(t) = \tilde{c}{\bf \tilde{x}(t)} \\
\tilde{A} = \left[
\begin{array}{rrrr}
\lambda_1 & 0 & \ldots & 0 \\
0 & \lambda_2 & \ldots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \ldots & \lambda_n
\end{array}
\right]
さらにこの式から次の式が成り立つことがわかります。
\tilde{x}'_i(t) = \lambda_i \tilde{x}_i(t) + \tilde{b}_i u(t) \\
y(t) = \sum_{i = 1}^n c_i \tilde{x}_i(t)
ただし、
{\bf \tilde{x}(t)} = (\tilde{x}_1(t), \tilde{x}_2(t), \cdots , \tilde{x}_n(t)) \\
{\bf \tilde{b}} = (\tilde{b}_1, \tilde{b}_2, \cdots , \tilde{b}_n) \\
{\bf \tilde{c}} = (\tilde{c}_1, \tilde{c}_2, \cdots , \tilde{c}_n) \\
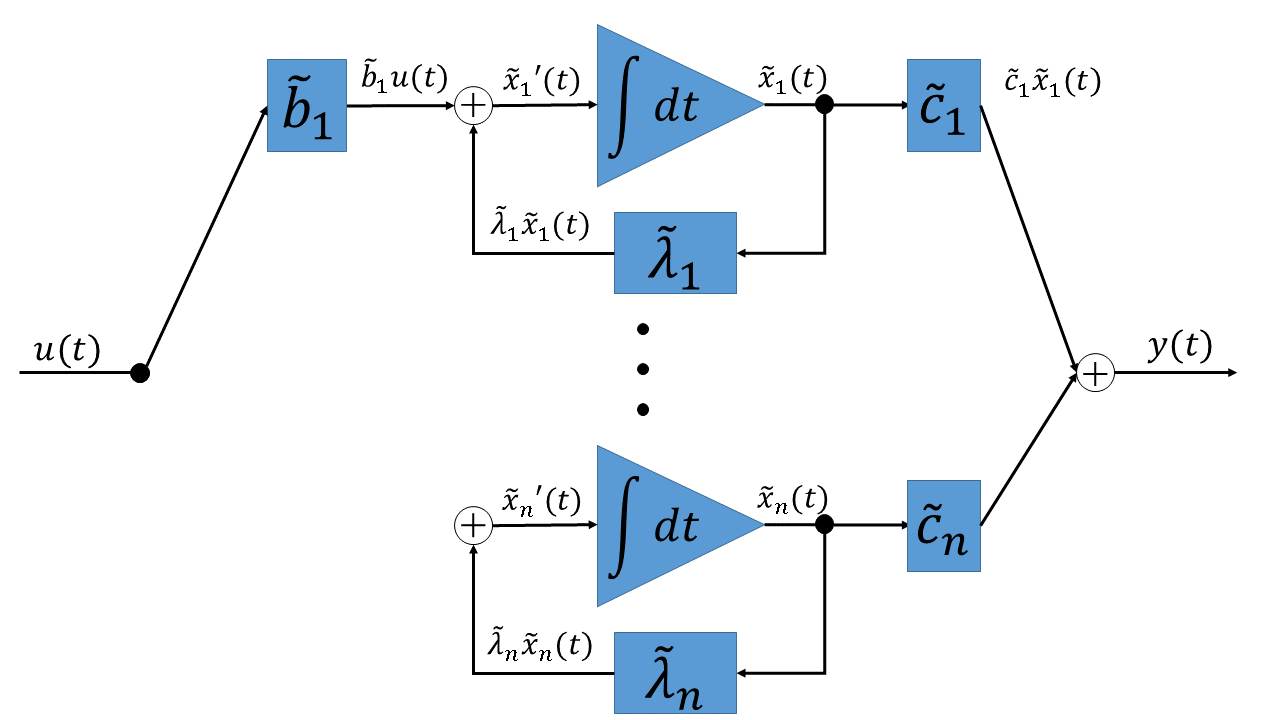
とします。固有値$\lambda_i$に対応する状態変数$\tilde{x}_i(t)$をモードといいます。この式から状態変数線図を書くと下図のようになります。
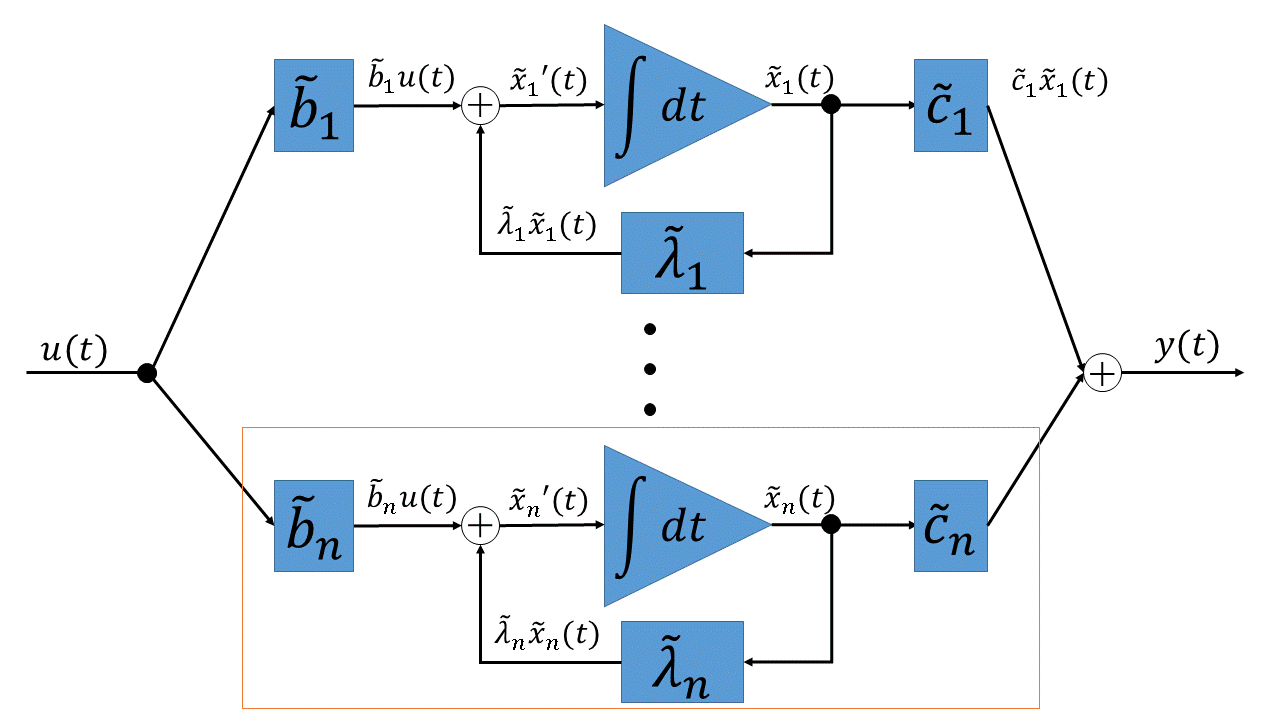
この図を見ると、各モードは互いに独立に入力を処理しその総和が出力になっていることがわかります。また、オレンジの枠で囲んだ部分をこのシステムのサブシステムといいますが、同じ形のサブシステムが並列に並んでシステムを構成していることもわかります。
そして$\tilde{x}_i(t)$に関する微分方程式を解けば、解は下式のようになります。(出力方程式は省略しています)
\tilde{x}_i(t) = \tilde{x}_i(0) e^{\lambda_i t} + \tilde{b}_i\int_0^t u(t)e^{\lambda_i(t - \tau)}d\tau
ただし${\bf \tilde{x}(0)} = (\tilde{x}_1(0), \cdots ,\tilde{x}_n(0))$とします。
上式を見ると、指数関数がありかつその指数に固有値が含まれていることがわかります。この形は、伝達関数を逆ラプラス変換した際にも出てきた形です。伝達関数での安定な条件を考えると、この固有値の値が安定性に影響すると予想できるでしょう。
次の項でこの式を用いてシステムの応答と安定性について考えていきます。
線形時不変システムの応答と安定性
前項で導かれた解を式Aとします。式Aは、2つの項に分かれておりそれぞれ名前がついています。
式Aの第1項を自由応答といい、第2項を零状態応答といいます。自由応答は、入力が存在しない場合のシステムの応答を表します。零状態応答は、初期値が存在しない場合のシステムの応答を表します。
式Aは第2項に積分があり少し複雑な形をしているので、まずは自由応答の場合すなわち入力がない場合の応答について見ていきましょう。
自由応答
入力が常に0である場合、式Aは下のようになります。ただし、今回は出力方程式を省略していません。
\tilde{x}_i(t) = \tilde{x}_i(0) e^{\lambda_i t} \\
y(t) = \sum_{i = 1}^n \tilde{c}_i \tilde{x}_i(0)e^{\lambda_i t}
前項でも少し書いたように、応答は固有値に大きく関係しています。これらの式を見ればそのことがよくわかるでしょう。固有値とそれに対応するモードは下のような関係になっています。
- $\lambda_i$の実部が正 -> 対応するモードは$t \to \infty$で発散
- $\lambda_i$の実部が負 -> 対応するモードは$t \to \infty$で0に収束
- $\lambda_i$の虚部が存在 -> 対応するモードは振動
出力はモードの和であるので、$\tilde{c}_i$の値にもよりますが少なくとも実部がすべて負であれば出力は発散しないことがわかります。
$\tilde{c}_i$の値にもよる、と言ったのは例えばあるモード$\tilde{x}_i$に対応する$\lambda_i$の実部が正であったとき、もしそのモードに対応する$\tilde{c}_i$が0であった場合には、$\tilde{c}_i\tilde{x}_i = 0$となるからです。このことについては後に詳しく説明します。
零状態応答
$\tilde{x}_i(0) = 0$、すなわち状態変数の初期値が0である場合式Aは下式のようになります。
\tilde{x}_i(t) = \tilde{b}_i\int_0^t u(t)e^{\lambda_i(t - \tau)}d\tau \\
y(t) = \sum_{i = 1}^n \tilde{c}_i \tilde{b}_i\int_0^t u(t)e^{\lambda_i(t - \tau)}d\tau
積分があり少し難しい形をしていますが、有界な入力に対してであれば固有値とモードの対応関係を調べることができます。
計算の詳細は省きますが、有界な入力に対する対応関係は自由応答の場合と同じ、つまり下の関係にあります。
- $\lambda_i$の実部が正 -> 対応するモードは$t \to \infty$で発散
- $\lambda_i$の実部が負 -> 対応するモードは$t \to \infty$で0に収束
- $\lambda_i$の虚部が存在 -> 対応するモードは振動
この場合も、$\tilde{b}_i$の値によって出力の発散、収束が変化しますが、少なくとも固有値の実部が負であれば出力は0に収束します。これは自由応答の場合と同じ理由によるものです。このことについても後で詳しく説明します。
線形時不変システムの安定性
自由応答と零状態応答でみたモードと固有値の関係から、線形時不変なシステムの安定性について次のことがわかります。ただし各モードに対応する$\tilde{b}_i, \tilde{c}_i$の値は全て0でないとします。
システム行列のすべての固有値の実部が負のとき、システムはBIBO安定である
しかし、厳密にいえばこの表現は適切ではありません。なぜなら、先に書いたように、固有値の実部が正、すなわちモードが発散する場合でも$\tilde{b}_i, \tilde{c}_i$の値によっては出力が収束する場合もあるからです。
このことは明らかに$\tilde{b}_i, \tilde{c}_i$の値に関係していることがわかるでしょう。これに関して、次に説明する可制御性と可観測性という考え方があり、結論から言うと上の定義は可制御でありかつ可観測である場合に成り立ちます。
可制御性と可観測性
可制御性と可観測性というのは、その名前から、入力によって「システムを制御」できるか、システムの出力が「観測できるか」ということではないかと予想できるでしょう。
実際イメージとしては大体その見方でよいと思います。では厳密な定義はどのようになっているのでしょうか。
今、状態方程式と出力方程式が対角正準形式に変換できたとします。このとき変換後の${\bf b} = (b_1, b_2, \cdots, b_n)$を${\bf \tilde{b}} = (\tilde{b}_1, \tilde{b}_2, \cdots, \tilde{b}_n)$とし、変換後の${\bf c} = (c_1, c_2, \cdots, c_n)$を${\bf \tilde{c}} = (\tilde{c}_1, \tilde{c}_2, \cdots, \tilde{c}_n)$とします。
システムが可制御であるというのは、全てのモードに対応する入力係数ベクトルの要素が0でない、ということです。
また、システムが可観測であるというのは、全てのモードに対応する出力係数ベクトルの要素が0でない、ということです。
式で書けば下のようになります。
\forall \tilde{b}_i \neq 0 \ (i = 1,2,\cdots,n) \\
\forall \tilde{c}_i \neq 0 \ (i = 1,2,\cdots,n)
可制御性というのはシステムが可制御であるかどうか、可観測性というのはシステムが可観測であるかどうかということです。
このように、定義は非常に簡単です。しかしこの考え方が、システムの出力の収束性に影響を及ぼします。このことは、状態変数線図を用いるとはっきりと理解できると思います。
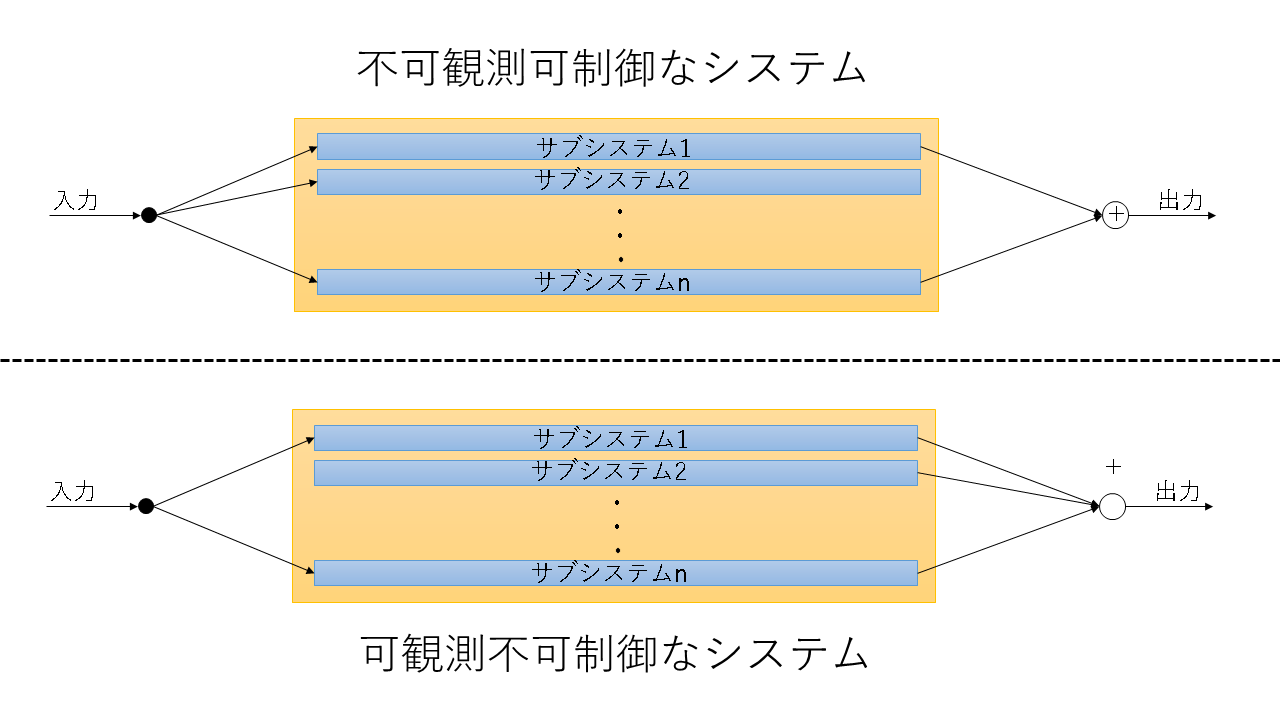
例えば、あるシステムが可制御であるが可観測でない(不可観測)場合、状態変数線図は下図のようになります。
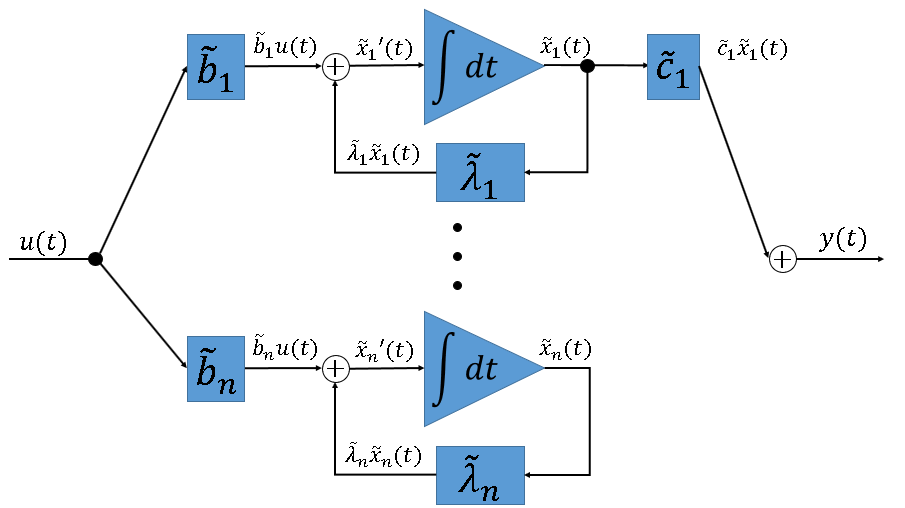
逆に、不可制御でかかつ可観測なシステムの場合、状態変数線図は下図のようになります。
これらの図から、不可制御の場合は入力がサブシステムに伝わっておらず、不可観測の場合はサブシステムの出力がシステムの出力に影響を及ぼしていないことがわかると思います。前項で、モードが発散する場合でもシステムの出力が収束することがある、と書きましたがこの場合がまさに不可制御または不可観測なシステムであるということです。
このように、不可制御なシステムでは入力がシステムに影響を全く与えないモードが存在し、不可観測なシステムではサブシステムの出力がシステムの出力に影響を与えないモードが存在する、ということがわかります。
この項の初めに書いた、可制御性=入力で制御可能ということと、可観測性=出力が観測できる、というイメージでだいたい合っているということも、上の状態変数線図を見ることでわかると思います。入力が出力に反映されなければ制御しても意味はないですし、出力が常に不明であれば観測することはできません。なお、このことは次の記事で書く予定の、フィードバック制御とオブザーバという制御の手法に関わってきます。
最後に、対角正準形式に変換可能なシステムは下の図に示す4種類に分類することができることを示しておきます。

システムの安定条件
前項で示したBIBO安定の条件で、可制御かつ可観測でなければいけないと付け加えた理由は、不可制御もしくは不可観測の場合には固有値の実部が正でもシステムの出力が収束してしまうからです。
よって、システムの安定性の必要十分条件を次のように再定義しておきましょう。
「システムが可制御かつ可観測である場合、システム行列の全ての固有値の実部が負であるならばそのシステムはBIBO安定である」
これと等価な安定条件は他にありますが、この記事では代表的な上の条件のみを書いておきます。気になる方は各自調べてみてください。
まとめ
この記事のまとめとして、次の3つをまとめておきます。
- システムのモデルの表し方の1つが状態空間表現で状態方程式を用いて表す。
- システムの安定条件はシステム行列の全ての固有値の実部が負であること。
- 可制御性と可観測性はシステムの入出力に影響を与える。
次回の記事ではフィードバック制御とオブザーバについて書く予定です。
今回も期日を守れずにすみませんでした。。。次の記事も遅れているのでなるべく早く書き上げます
参考文献
佐藤和也、下本陽一、熊澤典良『はじめての現代制御理論』講談社,2012年