ベイズ学習を書いてみた③

はじめに

前回は、１次元ガウス分布のベイズ学習について勉強しました。
今回は、多次元ガウス分布について勉強します。
（今回も教材として「ベイズ推論による機械学習」を使用します。）

多次元ガウス分布

１次元ガウス分布をより一般的な$D$ 次元に拡張した分布です。
（ベクトル${\bf x} \in \mathbb{R}^D$ を生成するための確率分布。）
多次元ガウス分布は以下の数式で表されます。

\mathcal N(x|\mu,\Sigma)=\frac{1}{\sqrt{(2\pi)^D|\Sigma|}}\exp\{-\frac{1}{2}({\bf x}-\mu)^{\mathrm{T}}\Sigma^{-1}({\bf x}-\mu)\}

対数を取ると次のようになります。

\ln \mathcal N(x|\mu,\Sigma)=-\frac{1}{2}\{({\bf x}-\mu)^{\mathrm{T}}\Sigma^{-1}({\bf x}-\mu)+\ln |\Sigma|+D\ln2\pi\}

以下の計算でも対数を取った式を使います。

尚、多次元ガウス分布もscipyライブラリを使って簡単に作れます。

import numpy as np
from scipy.stats import multivariate_normal
import matplotlib.pyplot as plt


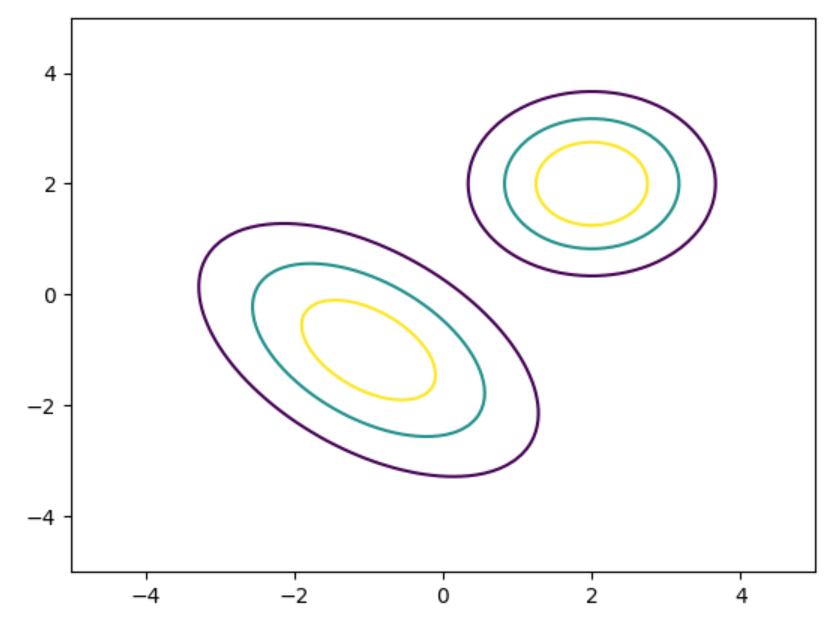
x, y = np.meshgrid(np.linspace(-5, 5, 100), np.linspace(-5, 5, 100))
z = np.dstack((x, y))

param_mean = [[-1.0, -1.0], [2.0, 2.0]]
param_cov = [[[2.0, 1.0], [-1.0, 2.0]], [[1.0, 0.0], [0.0, 1.0]]]

for mean, cov in zip(param_mean, param_cov):
    pdf = multivariate_normal.pdf(z, mean, cov)
    plt.contour(x, y, pdf, 3)
plt.show()

今回も下記の３つのパターンに分けて学習手順を整理します。

• 平均が未知
• 精度が未知
• 平均・精度が未知

※精度行列は共分散行列の逆行列（$\Lambda=\Sigma^{-1}$ と表記）

平均が未知

精度行列$\Lambda \in \mathbb{R}^{D×D}$ は既に与えられており、平均パラメータベクトル$\mu \in \mathbb{R}^D$ のみ推論します。
観測モデルは以下のようになります。

p({\bf x}|\mu)=\mathcal N({\bf x}|\mu,\Sigma^{-1}) \tag{1}

ガウス分布の平均パラメータは、同じくガウス分布を事前分布として用いることで解析的に推論できます。
ハイパーパラメータ$m\in \mathbb{R}^D$ および $\Lambda_\mu\in \mathbb{R}^{D×D}$ を与え、

p(\mu)= \mathcal N(\mu|m,\Sigma_\mu^{-1}) \tag{2}

とします。
(1), (2) を用いれば、$N$ 個のデータ ${\bf X}$ を観測した後の事後分布は以下のようになります。

\begin{align}
p(\mu|{\bf X})&\propto p({\bf X}|\mu)p(\mu)\\
&=\{\prod_{n=1}^Np({\bf x}_n|\mu)\}
p(\mu)\\
&=\{\prod_{n=1}^N\mathcal N({\bf x}_n|\mu,\Lambda^{-1})\}\mathcal N(\mu|m,\Lambda^{-1}_\mu) \tag{3}
\end{align}

対数を取ると以下のようになります。

\begin{align}
\ln p(\mu|{\bf X})&=\sum_{n=1}^N\ln \mathcal N({\bf x}_n|\mu, \Lambda^{-1})+\ln \mathcal N(\mu|m,\Lambda^{-1}_\mu) + const.\\
&=-\frac{1}{2}\{(\mu^{\mathrm{T}}(N\Lambda+\Lambda_\mu)\mu-2\mu^{\mathrm{T}}(\Lambda\sum_{n=1}^N{\bf x}_n+\Lambda_\mu m)\}+const. \tag{4}
\end{align}

１次元ガウス分布と同様に事後分布を新しいパラメータ$\hat{m}$ , $\hat{\Lambda}_\mu^{-1}$ で以下のように書きます。

p(\mu|{\bf X})=\mathcal N(\mu|\hat{m},\hat{\Sigma}^{-1}_\mu) 

この式に対数を取って$\mu$ に関して整理すれば、

\ln p(\mu|{\bf X})=-\frac{1}{2}\{\mu^{\mathrm{T}}\hat{\Lambda}_\mu\mu-2\mu^{\mathrm{T}}\hat{\Lambda}_\mu\hat{m}\}+const. \tag{5}

(4), (5) に関して$\hat{m}$ , $\hat{\Lambda}_\mu^{-1}$ の対応関係を取ると、

\begin{align}
\hat{\Lambda}_\mu&=N\Lambda+\Lambda_\mu\\
\hat{m}&=\hat{\Lambda}_\mu^{-1}(\Lambda\sum_{n=1}^N{\bf x}_n+\Lambda_\mu m)
\end{align}

と求められます。

pythonで書くと以下のよう書けます。

import numpy as np
from scipy.stats import multivariate_normal
import matplotlib.pyplot as plt

x, y = np.meshgrid(np.linspace(-5, 5, 100), np.linspace(-5, 5, 100))
z = np.dstack((x, y))

# parameter of prior gaussian distribution
hp_ms = [[-1.0, -1.0], [2.0, 0.0], [0.0, 2.0], [2.0, 2.0]]
hp_Sigmas = [[[2.0, 1.0], [1.0, 2.0]], [[0.2, 0.0], [0.0, 0.5]], [[3.0, 0.0], [0.0, 2.0]], [[2.0, -0.5], [-1.0, 2.0]]]

# parameter of posterior gaussian distribution
Lambda = np.array([[2.0, 0.0], [1.0, 2.0]])
mu = np.array([1.0, 1.0])

for i, (hp_m, hp_Sigma) in enumerate(zip(hp_ms, hp_Sigmas)):
    hp_m = np.array(hp_m)
    hp_Lambda = np.linalg.inv(np.array(hp_Sigma))
    plt.subplot(4, 4, i + 1)
    # m's prior gaussian distribution
    m = multivariate_normal.pdf(z, hp_m, hp_Lambda)
    plt.title('N=0', size=10)
    plt.contour(x, y, m, 3)
    plt.tick_params(labelleft='off')
    plt.tick_params(labelbottom='off')
    for j, N in enumerate([3, 10, 50]):
        plt.subplot(4, 4, 4 * (j + 1) + i + 1)
        # observed data
        X = multivariate_normal.rvs(mu, Lambda, N, random_state=1234)
        # plt.plot(X[:, 0], X[:, 1], "o", markersize=2, label='N=' + str(N))
        # update parameter
        new_Lambda = N * np.array(Lambda) + hp_Lambda
        sum_X = np.sum(X, axis=0)
        new_m = np.dot(np.linalg.inv(new_Lambda), (np.dot(Lambda, sum_X) + np.dot(hp_Lambda, hp_m)))
        # posterior distribution
        Sigma = np.linalg.inv(new_Lambda)
        pdf = multivariate_normal.pdf(z, new_m, Sigma)
        plt.title('N=' + str(N), size=10)
        plt.contour(x, y, pdf, 3)
        # plt.legend(loc="upper left")
        plt.tick_params(labelleft='off')
        plt.tick_params(labelbottom='off')
plt.show()

１行目（$N=0$ ）の分布は、観測データを与えていない状態（事前分布と同じ）です。
当然ですが、各分布はハイパーパラメータに依存しています。
今回も$N$ を増やすごとに分散が小さっていることが分かります。
４行目（$N=50$ ）の分布では、ハイパーパラメータの値に関わらず、どれもほとんど同じ分布となっていることが分かります。

精度が未知

観測モデルは以下のようになります。

p({\bf x}|\Sigma)=\mathcal N({\bf x}|\mu,\Sigma^{-1}) \tag{6}

「平均が未知」の場合と同様に、未知パラメータの確率分布を用意します。
今回は正定値行列である精度行列$\Sigma$ を生成する確率分布ですが、これは次のようなウィシャート分布を事前分布にとるのが望ましいです。

p(\Sigma)=\mathcal W(\Sigma|v, {\bf W})

${\bf W}$ ,$v$ はハイパーパラメータとして事前に設定しておきます。
ウィシャート分布は多次元ガウス分布の精度行列に関する共役事前分布であるため、いつものように事後分布のパラメータが計算可能です。

ウィシャート分布もscipyライブラリを使って作れます。

from scipy.stats import wishart, multivariate_normal
import numpy as np
import matplotlib.pyplot as plt

x, y = np.meshgrid(np.linspace(-5, 5, 100), np.linspace(-5, 5, 100))
z = np.dstack((x, y))

w = wishart(df=3, scale=np.array([[1.0, 0.5], [0.5, 1.0]]))
Lambdas = w.rvs(9, random_state=1234)

mu = [1.0, 1.0]

i = 1
for Lambda in Lambdas:
    plt.subplot(3, 3, i)
    Sigma = np.linalg.inv(Lambda)
    pdf = multivariate_normal.pdf(z, mu, Sigma)
    plt.contour(x, y, pdf, 3)
    plt.tick_params(labelleft='off')
    plt.tick_params(labelbottom='off')
    i += 1
plt.show()

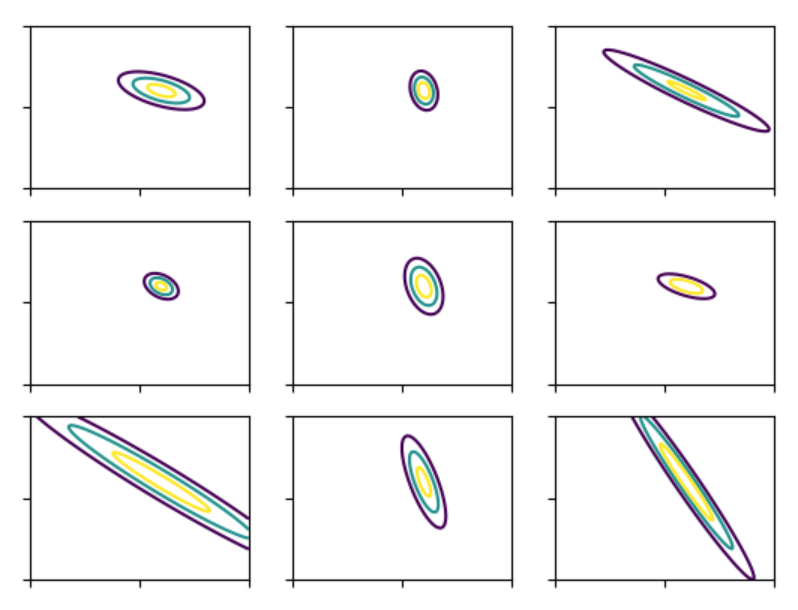ウィシャート分布が生成する精度行列によって多次元ガウス分布の分布が異なっていることが分かります。

途中の計算は省略しますが、観測データから次のような精度行列パラメータは

p(\Sigma|{\bf X})=\mathcal W(\Sigma|\hat{v},\hat{{\bf W}})

\begin{align}
\hat{{\bf W}}^{-1}&=\sum_{n=1}^N({\bf x}_n-\mu)({\bf x}_n-\mu)^{\mathrm{T}}+{\bf W}^{-1}\\
\hat{v}&=N+v
\end{align}

となります。
pythonで書くと以下のよう書けます

from scipy.stats import wishart, multivariate_normal
import numpy as np

x, y = np.meshgrid(np.linspace(-5, 5, 100), np.linspace(-5, 5, 100))
z = np.dstack((x, y))

# parameter of prior wishart distribution
hp_Ws = [[[0.5, 1.0], [0.5, 1.5]], [[5.0, 0.0], [0.0, 2.0]], [[0.3, 0.0], [0.0, 0.5]], [[0.5, -0.5], [-1.0, 1.5]]]
hp_vs = [2, 3, 4, 5]

# parameter of posterior gaussian distribution
Lambda = np.array([[1.0, 0.5], [0.5, 2.0]])
mu = np.array([1.0, 1.0])

for i, (hp_v, hp_W) in enumerate(zip(hp_vs, hp_Ws)):
    for j, N in enumerate([3, 10, 50]):
        # observed data
        X = multivariate_normal.rvs(mu, Lambda, N, random_state=1234)
        # update parameter
        sum_xu = np.matrix(np.sum(X - mu, axis=0)).reshape(2, 1)
        new_W_inv = (sum_xu * sum_xu.T) + np.linalg.inv(hp_W)
        new_v = N + hp_v
        # posterior distribution
        new_Lambda = wishart.rvs(df=new_v, scale=np.linalg.inv(new_W_inv), size=N)

事後分布は、ウィシャート分布が生成する精度行列の確率分布となるため、二次元で描画は出来ません。
なので、今回は計算だけです。

平均・精度が未知

観測モデルは以下のようになります。
事前分布にガウス・ウィシャート分布を使えば、事後分布が同じ形式で得られます。

\begin{align}
p(\mu,\Lambda)&={\rm NW}(\mu,|\Lambda|m, \beta, v, {\bf W})\\
&=\mathcal N(\mu, |m,(\beta\Lambda)^{-1})\mathcal W(\Lambda|v, {\bf W})
\end{align}

グラフィカルモデルは少しややこしいですが、以下のようになります。

$\mu$ ,$\Lambda$ の事後分布は条件付き分布によって以下のように分解できます。

p(\mu, \Lambda|{\bf X})=p(\mu|\Lambda,{\bf X})p(\Lambda|{\bf X})

$p(\mu|\Lambda,{\bf X})$ に関しては平均が未知の場合と同様の手順で以下のように算出できます。

\begin{align}
p(\mu|\Lambda,{\bf X})=\mathcal N(\mu|\hat{m},(\hat{\beta}\Lambda)^{-1})
\end{align}

\begin{align}
\hat{\beta}&=N+\beta\\
\hat{m}&=\frac{1}{\hat{\beta}}(\sum_{n=1}^N{\bf x}_n+\beta m)
\end{align}

$p(\Lambda|{\bf X})$ に関しては分散が未知の場合と同様の手順で以下のように算出できます。

\begin{align}
p(\Lambda|{\bf X})=\mathcal W(\Lambda|\hat{v},(\hat{{\bf W}})
\end{align}

\begin{align}
\hat{\bf W}^{-1}&=\sum_{n=1}^N{\bf x}_n{\bf x}_n^{\mathrm{T}}+\beta mm^{\mathrm{T}}-\hat{\beta}\hat{m}\hat{m}^{\mathrm{T}}+{\bf W}^{-1}\\
\hat{v}&=N+v
\end{align}

pythonで書くと以下のよう書けます

from scipy.stats import wishart, multivariate_normal
import numpy as np

x, y = np.meshgrid(np.linspace(-5, 5, 100), np.linspace(-5, 5, 100))
z = np.dstack((x, y))

# hyper parameter of prior distribution
hp_m = np.array([0.0, 0.0])
hp_beta = 2.0
hp_W = np.array([[0.5, 1.0], [0.5, 1.5]])
hp_v = 2.0
# parameter of posterior gaussian distribution
Sigma = np.array([[1.0, 0.5], [0.5, 2.0]])
mu = np.array([1.0, 1.0])

for j, N in enumerate([3, 10, 50]):
    # observed data
    X = multivariate_normal.rvs(mu, Sigma, N, random_state=1234)
    # update parameter
    sum_x = np.matrix(np.sum(X, axis=0))
    new_beta = N + hp_beta
    new_m = (1 / new_beta) * (sum_x + hp_beta * hp_m)
    hp_m_ = np.asmatrix(hp_m).reshape(2, 1)
    new_m_ = np.asmatrix(new_m).reshape(2, 1)
    X_ = np.matrix(X).reshape(2, N)
    new_W_inv = (X_ * X_.T) + (hp_beta * hp_m_ * hp_m_.T) - (new_beta * new_m_ * new_m_.T) + np.linalg.inv(hp_W)
    new_v = N + hp_v
    # posterior distribution
    new_Lambda = wishart.rvs(df=new_v, scale=np.linalg.inv(new_W_inv), size=N)
    new_mu = multivariate_normal.pdf(z, np.squeeze(np.asarray(new_m)), np.linalg.inv(new_beta * new_Lambda))

ただし、最後の$\mu$ の分布を求めるところで以下のエラーで落ちます。。

ValueError: Array 'cov' must be at most two-dimensional, but cov.ndim = 3

これは、分散行列$\hat{\beta}\Lambda^{-1}$が行列でなくテンソルの形になっていることが原因です。
つまり、分散行列は分布の形では受け取ってくれません。。
（１次元ガウス分布の場合の分散は固定値でなくても大丈夫でしたが・・）

scipyでも他のやり方で対応できるかもしれませんが、それはまた別の機会に考えます。

最後のところで中途半端になってしまいましたが、コードを書いてベイズ推論の理解を深めることは出来たので良しとします。。