ベイズ学習を書いてみた②

はじめに

前回は、離散分布（ベルヌーイ分布）のベイズ学習について勉強しました。
今回は、連続確率分布について勉強します。
今回は理解しやすい１次元ガウス分布をベイズ学習します。
（今回も教材として「ベイズ推論による機械学習」を使用させて頂いております。）

１次元ガウス分布

確率密度関数は以下の通りです。

\mathcal N(x|\mu,\sigma^2)=\frac{1}{\sqrt {2\pi\sigma^2}}\exp\{-\frac{(x-\mu)^2}{2\sigma^2}\}

対数を取ると以下になります。

\ln \mathcal N(x|\mu,\sigma^2)=-\frac{1}{2}\{-\frac{(x-\mu)^2}{\sigma^2}+\ln \sigma^2 + \ln 2\pi\}

１次元ガウス分布も前回と同じでscipyライブラリを使って簡単に作れます。

import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt

mu, sigma = 0, 1.0  # mean and standard deviation

x = np.linspace(-5, 5, 500)
y = norm.pdf(x=x, loc=mu, scale=sigma)
plt.plot(x, y, '-', lw=2)
plt.show()

学習は３つのパターンに分かれます。

• 平均が未知
• 精度が未知
• 平均・精度が未知

※精度は分散の逆数（$\lambda=\sigma^{-2}$ と表記）

それぞれのパターンについて書いていきます。

平均が未知の場合

推定するのは、平均値$\mu$ となります。今回、精度$\lambda$ は固定します。

学習

個々の観測データで、以下の条件付き分布を考えます。

p(x|\mu)=\mathcal N(x|\mu,\lambda^{-1})\tag{1}

$\mu$ の共役事前分布として次のようなガウス分布となることが知られています。

p(\mu)=\mathcal N(\mu|m,\lambda^{-1}_\mu)

パラメータ$m,\lambda^{-1}_\mu$ を動かすと、$\mu$ の分布は以下のように変化します。

import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt

# parameter of prior gaussian distribution
params = [[-1.0, 1.0], [1.0, 1.0], [0.0, 2.0], [0.0, 3.0]]

for i, param in enumerate(params):
    m, sigma_ = param[0], param[1]
    mu = norm.pdf(x=x_, loc=m, scale=sigma_)
    plt.plot(x_, mu, '-', lw=2, label='mu=' + str(m) + ' scale=' + str(sigma_))
    plt.legend(loc="upper right")
plt.show()

$N$ 個の１次元連続データ${\bf X}$ を使って、事後分布は次のように書けます。

\begin{align}
p(\mu|{\bf X})&\propto p({\bf X}|\mu)p(\mu)\\
&=\{\prod_{n=1}^Np(x_n|\mu)\}
p(\mu)\\
&=\{\prod_{n=1}^N\mathcal N(x_n|\mu,\lambda^{-1})\}\mathcal N(\mu|m,\lambda^{-1}_\mu)
\end{align}

前回と同様にこの分布の対数を取って計算します。

\begin{align}
\ln p(\mu|{\bf X})&=\sum_{n=1}^N\ln \mathcal N(x_n|\mu,\lambda^{-1}) + \ln \mathcal N(\mu|m,\lambda^{-1}_\mu) + const.\\
&=-\frac{1}{2}\{(N\lambda+\lambda_\mu)\mu^2-2(\sum_{n=1}^N x_n\lambda+m\lambda_\mu)\mu\}+const. \tag{2}
\end{align}

次に事後分布が以下で表せるとします。

p(\mu|{\bf X})= \mathcal N(\mu|\hat{m},\hat{\lambda}^{-1}_\mu)

これの対数を取り、式を整理すると以下のように書けます。

\ln p(\mu|{\bf X})=-\frac{1}{2}\{\hat{\lambda}_\mu\mu^2-2\hat{m}\hat{\lambda}_\mu\mu\}+const. \tag{3}

これを(2)との係数の対応関係を取ることで、事後分布のパラメータは以下のように決まります。

\begin{align}
\hat{\lambda}_\mu&=N\lambda+\lambda_\mu \\
\hat{m}&=\frac{\lambda\sum_{n=1}^Nx_n+\lambda_\mu m}{\hat{\lambda}_\mu}
\end{align}

これで、事前分布と観測データを用いて事後分布が求められることが分かりました。

pythonで書くとベイズ学習は以下のよう書けます。

import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt

x_ = np.linspace(-8, 8, 500)
# parameter of prior gaussian distribution
params = [[-1.0, 0.1], [1.0, 1.0], [-1.0, 0.1], [1.0, 1.0]]

lambda_ = 0.25  # parameter of gaussian distribution

for i, param in enumerate(params):
    plt.subplot(4, 4, i + 1)
    m, p_lambda_ = param[0], param[1]
    sigma_ = np.sqrt(np.reciprocal(p_lambda_))
    mu = norm.pdf(x=x_, loc=m, scale=sigma_)
    plt.plot(x_, mu, '-', lw=1)
    plt.title('m=' + str(m) + ' p_lambda=' + str(p_lambda_), size=10)
    plt.tick_params(labelleft='off')
    for j, N in enumerate([3, 10, 50]):
        plt.subplot(4, 4, 4 * (j + 1) + i + 1)
        x = norm.rvs(loc=0, scale=1, size=N)  # observed data
        sum_x = np.sum(x)
        lambda_ = N * p_lambda_ + lambda_  # update lambda
        m_ = (lambda_ + sum_x + p_lambda_ * m) / lambda_  # update m
        sigma_ = np.sqrt(np.reciprocal(lambda_))  # calculate scale
        X = norm.pdf(x=x_, loc=m_, scale=sigma_)
        plt.plot(x_, X, '-', lw=1, label='N=' + str(N))
        plt.legend(loc="upper right")
        plt.tick_params(labelleft='off')
plt.show()

前回と同様に$N$を変えながら事後分布を確認しました。
$N$ の数が増えるほど、鋭い凸型になっている（精度が高くなる）のが分かります。

予測

未観測データ$x_*$ の予測分布を確認します。
これは、次のような周辺分布を計算することに対応します。

\begin{align}
p(x_*)&=\int p(x_*|\mu)p(\mu){\rm d}\mu\\
&=\int \mathcal N (x_*|\mu,\lambda^{-1})\mathcal N (\mu|m,\lambda_\mu^{-1}){\rm d}\mu
\end{align}

求めたい予測分布は、ベイズの定理より以下のように求めることができます。

p(\mu|x_*)=\frac{p(x_*|\mu)p(\mu)}{p(x_*)}\\
p(x_*)=\frac{p(x_*|\mu)p(\mu)}{p(\mu|x_*)}

対数を取ると以下のようになります。

\ln p(x_*)=\ln p(x_*|\mu) - \ln p(\mu|x_*) + const.

上式では、$\ln p(\mu)$ は変数$x_*$ とは無関係なので定数に入れています。
$p(\mu|x_*)$ は(3)式の${\bf X}$ を$x_*$ に置き換えると計算できます。
$p(x_*|\mu)$ は(1)式そのものです。

途中の導出過程は省略しますが、最終的に予測分布は以下のようになります。
（詳細は「ベイズ推論による機械学習」でご確認ください。）

p(X*)=\mathcal N (x_*|\mu_*,\lambda^{-1}_*)

\begin{align}
\lambda_*&=\frac{\lambda\lambda_\mu}{\lambda+\lambda_\mu}\\
\mu_*&=m
\end{align}

また、$N$ 個のデータを観測した後の予測分布$p(x_*|{\bf X})$ を求めたい場合、事前分布のパラメータ$m$ および$\lambda_\mu$ の代わりに、事後分布のパラメータ$\hat{m}$ および$\hat{\lambda}_\mu$ を用いることで得られます。

精度が未知の場合

精度$\lambda$ の両方を計算します。平均値$\mu$ は固定します。

学習

観測データの条件付き分布は以下となります。

p(x|\lambda)=\mathcal N (x|\mu,\lambda^{-1})

$\lambda$ の分布ですが、平均が未知の時の正規分布ではなく、正の実数値をとるガンマ分布を仮定するのが自然です。

p(\lambda)={\rm Gam}(\lambda|a,b)

ガンマ分布ですが、scipyを使って作るのが簡単です。
ガンマ分布は以下のようにして作れます。

import numpy as np
from scipy.stats import gamma
from matplotlib import pyplot as plt

x = np.linspace(0, 10, 1000)
# params = [[6, 6], [7, 5], [8, 4], [5, 7], [4, 8]]
params = [[1.0, 1.0], [2.0, 2.0], [2.0, 0.5]]
for param in params:
    alpha_, beta_ = param[0], param[1]
    y = gamma.pdf(x=x, a=alpha_, scale=np.reciprocal(beta_))
    plt.plot(x, y, '-', lw=2, label=param)
    plt.legend()
plt.show()

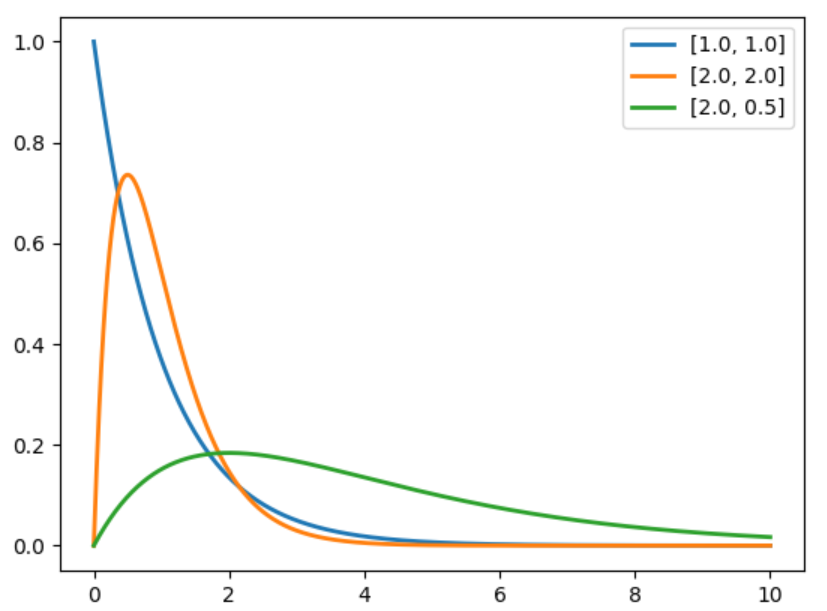
上の式に合わせる場合、np.reciprocal(beta_) で逆数を取る必要があります。

$\lambda$の事後分布は下記のようになります。

\begin{align}
p(\lambda|{\bf X})&\propto p({\bf X}|\lambda)p(\lambda)\\
&=\{\prod_{n=1}^N p(x_n|\lambda)\}p(\lambda)\\
&=\{\prod_{n=1}^N \mathcal N (x_n|\mu,\lambda^{-1})\}{\rm Gam}(\lambda|a,b)
\end{align}

対数を取ると下記のようになります。

\begin{align}
\ln p(\lambda|{\bf X})&= \sum_{n=1}^N\ln \mathcal N(x_n|\mu,\lambda^{-1})+\ln {\rm Gam}(\lambda|a,b) + const.\\
&=(\frac{N}{2}+a-1)\ln \lambda - \{\frac{1}{2}\sum_{n=1}^N(x_n-\mu)^2 + b \}\lambda + const.
\end{align}

$\lambda$ と$\ln \lambda$ にかかる係数部分に注目すれば、事後分布は以下のようなガンマ分布になります。

p(\lambda|{\bf X})={\rm Gam}(\lambda|\hat{a},\hat{b})

\begin{align}
\hat{a}&=\frac{N}{2}+a \\
\hat{b}&=\frac{1}{2}\sum_{n=1}^N(x_n-\mu)^2 + b
\end{align}

これで、精度が未知の場合も、事前分布と観測データを用いて事後分布が求められることが分かりました。

pythonで書くとベイズ学習は以下のよう書けます。

import numpy as np
from scipy.stats import norm, gamma
import matplotlib.pyplot as plt

x_ = np.linspace(-8, 8, 100)
# parameter of prior gamma distribution
params = [[1.0, 1.0], [2.0, 0.5], [2.0, 1.0], [3.0, 0.5]]

mu_ = 0  # parameter of gaussian distribution

for i, param in enumerate(params):
    plt.subplot(4, 4, i + 1)
    a_, b_ = param[0], param[1]
    p_lambda_ = gamma.pdf(x=x_, a=a_, scale=np.reciprocal(b_))  # prior distribution
    sigma_ = np.sqrt(np.reciprocal(p_lambda_))
    plt.plot(x_, sigma_, '-')
    plt.title('a=' + str(a_) + ' b=' + str(b_) , size=10)
    plt.tick_params(labelleft='off')
    for j, N in enumerate([3, 10, 50]):
        plt.subplot(4, 4, 4 * (j + 1) + i + 1)
        x = norm.rvs(loc=1, scale=1, size=N)  # observed data
        sum_x = np.sum(x)
        a = (N / 2) + a_  # update a
        b = 0.5 * np.sum(x - mu_) ** 2 + b_  # update b
        lambda_ = gamma.pdf(x=x_, a=a, scale=np.reciprocal(b))  # parameter lambda distribution
        sigma_ = np.sqrt(np.reciprocal(lambda_))  # calculate scale
        X = norm.pdf(x=x_, loc=mu_, scale=sigma_)  # posterior distribution
        plt.plot(x_, X, '-', lw=1, label='N=' + str(N))
        plt.legend(loc="upper right")
        plt.tick_params(labelleft='off')
plt.show()

最初の分布は、観測データを与えていないので、事前分布で用いたガンマ分布そのものとなります。
これも今まで通り、$N$ を増やすことで、事後分布は、$\mu=0$ の真の分布に近づいていることが分かります。

予測

予測分布$p(x_*)$ は次のような積分計算によって導かれます。

p(x_*)=\int p(x_*|\lambda)p(\lambda){\rm d}\lambda

導出過程は少し長くなるので省略しますが、最終的な形は「スチューデントのt分布」に対数をとった次の式になることが知られています。

\begin{eqnarray}
\ln {\rm St}(x|\mu_s,\lambda_s, v_s)=-\frac{v_s+1}{2}\ln\{1+\frac{\lambda_s}{v_s}(x-\mu_s)^2\}^{-\frac{v_s+1}{2}}
\end{eqnarray}

まとめると以下のように書けます。

p(x_*)={\rm St}(x|\mu_s,\lambda_s, v_s)

\begin{align}
\mu_s&=\mu\\
\lambda_s&=\frac{a}{b}\\
v_s&=2a
\end{align}

平均・精度が未知の場合

平均値$\mu$ および精度$\lambda$ の両方を計算します。

学習

観測データの条件付き分布は以下となります。

p(x|\mu,\lambda)=\mathcal N (x|\mu,\lambda^{-1})

１次元ガウス分布では、次のような$m,\beta,a,b$ を固定パラメータとした「ガウス・ガンマ分布」を事前分布と仮定すると、まったく同じ形式の事後分布が得られることが知られています。

\begin{align}
p(\mu,\lambda)&={\rm NG}(\mu,\lambda|m,\beta,a,b)\\
&=\mathcal N(\mu|m,(\beta\lambda)^{-1}){\rm Gam}(\lambda|a,b)
\end{align}

平均が未知の場合と同様に事後分布における４つのハイパーパラメータ$\hat{m},\hat{\beta},\hat{a},\hat{b}$ を求めるのが学習の目標となります。

ここで、グラフィカルモデルを確認します。

精度$\lambda$ は平均$\mu$ の親であることが分かります。
つまり、**平均$\mu$ の分布を求めるためには、精度$\lambda$ が必要であるということです。

まず、平均$\mu$ に関する事前分布から見ていきます。
この事後分布は「平均が未知の場合」と同じ手順で以下のように計算できます。

p(\mu|\lambda,{\bf X})=\mathcal N(\mu|\hat{m},(\hat{\beta}\lambda)^{-1})

\begin{align}
\hat{\beta}&=N+\beta\\
\hat{m}&=\frac{1}{\hat{\beta}}(\sum_{n=1}^Nx_n+\beta m)
\end{align}

次に精度$\lambda$ に関するパラメータ\hat{a},\hat{b}$ を求めます。
これも、「精度が未知の場合」の場合と同じ手順で以下のように計算できます。

p(\lambda|{\bf X})={\rm Gam}(\lambda|\hat{a},\hat{b})

\begin{align}
\hspace{3.5cm} \hat{a}&=\frac{N}{2}+a \\
\hat{b}&=\frac{1}{2}\sum_{n=1}^N(x_n^2+\beta m^2-\hat{\beta}\hat{m}^2) + b
\end{align}

pythonで書くとベイズ学習は以下のよう書けます。

import numpy as np
from scipy.stats import norm, gamma
import matplotlib.pyplot as plt

x_ = np.linspace(-8, 8, 100)
# parameter of prior distribution
ps_m = [-1, 0, 1, 2]
ps_beta = [1, 2, 3, 4]
ps_ab = [[1.0, 1.0], [2.0, 0.5], [2.0, 1.0], [3.0, 0.5]]


def calc_a(p_N=0, p_a=0.0):
    return (p_N / 2) + p_a


def calc_b(x_=np.array([0]), beta_hat=0.0, m_hat=0.0, p_beta=0.0, p_m=0.0, p_b=0.0):
    return 0.5 * (np.sum(x_ ** 2) + (p_beta * p_m ** 2) - (beta_hat * m_hat ** 2)) + p_b


def calc_beta(p_N=0, p_beta=0.0):
    return p_N + p_beta


def calc_m(x_=np.array([0]), beta_hat=0.0, p_beta=0.0, p_m=0.0):
    return 1 / beta_hat * (np.sum(x_) + p_beta * p_m)


for i, (m_, beta_, ab_) in enumerate(zip(ps_m, ps_beta, ps_ab)):
    plt.subplot(4, 4, i + 1)
    a_, b_ = ab_[0], ab_[1]
    # update parameter without observed data
    beta_hat = calc_beta(p_beta=beta_)
    m_hat = calc_m(beta_hat=beta_hat, p_beta=beta_, p_m=m_)
    a_hat = calc_a(p_a=a_)
    b_hat = calc_b(beta_hat=beta_hat, p_beta=beta_, p_m=m_, p_b=b_)
    # parameter lambda distribution
    p_lambda_ = gamma.pdf(x=x_, a=a_, scale=np.reciprocal(b_))
    sigma_ = np.sqrt(np.reciprocal(p_lambda_))
    # parameter mu distribution
    mu_ = norm.pdf(x=x_, loc=m_hat, scale=sigma_)
    plt.plot(x_, mu_, '-')
    plt.title('a=' + str(a_) + ' b=' + str(b_), size=10)
    plt.tick_params(labelleft='off')
    for j, N in enumerate([3, 10, 50]):
        plt.subplot(4, 4, 4 * (j + 1) + i + 1)
        x = norm.rvs(loc=1, scale=1, size=N)  # observed data
        # update parameter with observed data
        beta_hat = calc_beta(p_N=N, p_beta=beta_)
        m_hat = calc_m(x_=x, beta_hat=beta_hat, p_beta=beta_, p_m=m_)
        a_hat = calc_a(p_N=N, p_a=a_)
        b_hat = calc_b(x_=x, beta_hat=beta_hat, m_hat=m_hat, p_beta=beta_, p_m=m_, p_b=b_)
        # parameter lambda distribution
        lambda_ = gamma.pdf(x=x_, a=a_hat, scale=np.reciprocal(b_hat))
        sigma_ = np.sqrt(np.reciprocal(lambda_))  # calculate scale
        X = norm.pdf(x=x_, loc=m_hat, scale=sigma_)  # posterior distribution
        plt.plot(x_, X, '-', lw=1, label='N=' + str(N))
        plt.legend(loc="upper right")
        plt.tick_params(labelleft='off')
plt.show()

今回も$N$ が十分に存在すると、事後分布が$\mu=0$ の真の分布に近づいていることが確認できました。

予測

予測分布$p(x_*)$ は次のような積分計算によって導かれます。
今回は、平均と精度の２つの変数を積分除去する必要があります。

p(x_*)=\int \int p(x_*|\mu, \lambda)p(\mu, \lambda){\rm d}\mu{\rm d}\lambda

この導出も「精度が未知の場合」の場合と同じ手順で以下のように計算できます。

p(x_*)={\rm St}(x|\mu_s,\lambda_s, v_s)

\begin{align}
\mu_s&=m\\
\lambda_s&=\frac{\beta a}{(1+\beta)b}\\
v_s&=2a
\end{align}

以上のように全ての分布が解析的に求めることができました。

さいごに

今回、式の導出をいくつか省略しましたので、詳しく知りたい方は書籍にてご確認ください。
次回は「多次元ガウス分布」に関するベイズ学習と予測を確認したいと思います。

後、今回のコードは、ここに置きました。