はじめに
最近の勉強のメインはニューラルネットです。
NLPの最近の論文もニューラルネットによるものが多いです。
なので、ニューラルネットのライブラリの使い方などの勉強は必要ですが、
最近はニューラルネットだけでなく、もう少し視野を広げたいなと思ってました。
(ニューラルネットの多種多様なモデルを理解する能力と気力が無いのもありますが・・)
そんな時「トピックモデルによる統計的潜在意味解析」を読んで、ベイズ学習に興味を持ちました。
もう少し勉強したいと思い「ベイズ推論による機械学習入門」を読み始めました。
まだまだ素人ですが、読んだ内容をアウトプットしようと思いコードを書いてみました。
今回は、最初の方に出てくる「ベルヌーイ分布のベイズ学習」に関してです。
事後分布が解析的に計算可能であるため、比較的簡単に書けました。
やりたいこと
ベイズ学習の目標は、あるモデルを作ってその事後分布を得ることです。
まず、パラメータに関する事前分布と学習データを用意します。
そこから、学習データとパラメータの事後分布を計算します。
式で表すと以下の通りです。(ベイズの定理)
\begin{align}
p(\theta|X)&=\frac{p(X|\theta)p(\theta)}{p(X)}\\
&\propto p(X|\theta)p(\theta)
\end{align}
$p(\theta)$ がパラメータの事前分布です。
ベルヌーイ分布
二値をとる値を生成するための確率分布です。
コインを投げたときの裏・表の出る確率分布とかのやつです。
ベルヌーイ分布は以下の式の通りです。
Bern(x|\mu)=\mu^x(1-\mu)^{1-x}
*$x \in [0,1], \mu$ はパラメータ
実際は対数変換した以下の式で計算することが多いです。
\ln Bern(x|\mu)=x\ln\mu+(1-x)\ln(1-\mu)
pythonでは、ライブラリscipyを使うと簡単に作れます。
from scipy.stats import bernoulli
print bernoulli.rvs(0.3, size=10)
# [0 0 0 0 1 0 0 0 1 1]
ベータ分布
ベルヌーイ分布の共役事前分布です。
上の$\mu$ の分布です。
Beta(\mu|a,b)=C_B(a,b)\mu^{a-1}(1-\mu)^{b-1}\\
* C_B=\frac{\Gamma(a+b)}{\Gamma(a)+\Gamma(b)}
パラメータは、$a,b$ の2つです。
これらは、ハイパーパラメータと呼ばれ、今回は事前に設定します。
ベータ分布を対数変換すると以下の式となります。
\ln Beta(\mu|a,b)=(a-1)\ln \mu + (b-1)\ln(1-\mu)+\ln C_B(a,b)
ベータ分布もscipyを使うと簡単に作れます。
import numpy as np
from scipy.stats import beta
from matplotlib import pyplot as plt
x = np.linspace(0, 1, 1000)
params = [[1, 1], [3, 3], [6, 6], [8, 4], [3, 7]]
for param in params:
alpha_, beta_ = param[0], param[1]
rv = beta(alpha_, beta_)
y = rv.pdf(x)
plt.plot(x, y, '-', lw=2, label=param)
plt.legend()
plt.show()
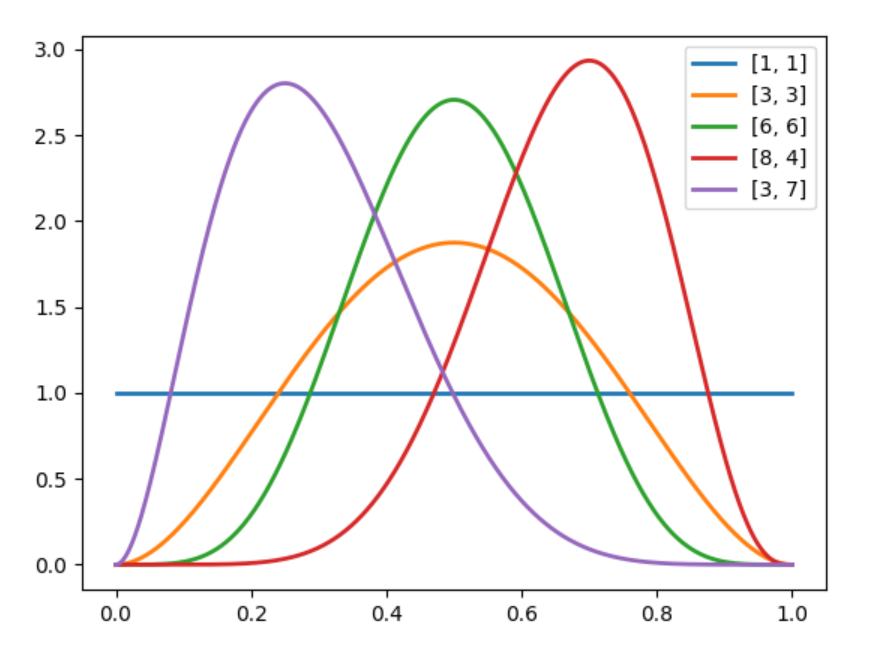
パラメータは、$a,b$ を変えると分布が大きく変わっていることが分かります。
ベータ分布の式を見ると、$a$ は$\mu$ に、$b$ は$(1-\mu)$ にの肩に掛っていることが分かります。
これは、ベルヌーイ分布の式と同じ形です。
このことより、$a$ は、$x=1$ に、$b$ は、$x=0$ に影響を及ぼすパラメータであることが分かります。
$a=1, b=1$ の場合、一様分布(それぞれ$-1$ するので)となります。
$a=3, b=3$ の場合、$P=0.5$ がピークとなる分布になります。
つまり、$x$ がどちらの値を取るかの偏っていない状態です。
$a=3, b=7$ の場合、$P=0.3$ あたりがピークとなります。
この場合、ベルヌーイ試行が$x=0$ が出やすいようなパラメータ分布となります。
今回は、ベータ分布のパラメータ$a,b$ を変えながら事後分布をみていきます。
グラフィカルモデル
確率分布のパラメータの関係性をノードと矢印を使って表現する方法です。
今回はシンプルなモデルですが、最初なので書いてみました。
データの発生に関係するパラメータは$\mu$ で、その$\mu$ の分布に関係するパラメータが$a,b$ であるということが分かります。($a,b$ を事前に与える場合、グラフィカルモデルに記述しなくても問題ありません。)
事後分布の計算
以下の式で計算できます。
\begin{align}
p(\mu|X)&=\frac{p(X|\mu)p(\mu)}{p(X)}\\
&=\frac{\{\prod_{n=1}^Np(x_n|\mu)\}p(\mu)}{p(X)}\\
&\propto \{\prod_{n=1}^Np(x_n|\mu)\}p(\mu)
\end{align}
上式を対数変換して計算を行っていきます。
\begin{align}
\ln p(\mu|X)&=\sum_{n=1}^N\ln p(x_n|\mu)+\ln p(\mu)+const.\\
&=\sum_{n=1}^Nx_n\ln \mu + \sum_{n=1}^N(1-x_n)\ln(1-\mu)\\
&+(a-1)\ln\mu+(b-1)\ln(1-\mu)+const.\\
&=(\sum_{n=1}^Nx_n+a-1)\ln\mu+(N-\sum_{n=1}^Nx_n+b-1)\ln(1-\mu)+const.
\end{align}
※この計算は、「ベイズ推論による機械学習入門」のまんまです。
計算すると、ベータ分布の対数変換した式とそっくりとなります。
\hat {a}=\sum_{n=1}^Nx_n+a\\
\hat {b}=N-\sum_{n=1}^Nx_n+b
とおくと、
p(\mu|X)=Beta(\mu|\hat{a},\hat{b})
のようなベータ分布として事後分布が表現できることが分かります。
では、実際にこれを計算するプログラムを書いてみます。
書いてみた
事前分布と観測データを与えたときの分布の様子を見てみます。
観測データ数を$5,20,100$ と増やして事後分布がどう変化するかを見ていきます。
学習部分は以下の感じです。
X = bernoulli.rvs(p, size=N) # 観測データの作成
xn = len(np.where(X == 1)[0]) # x=1の数
alpha_ = xn + alpha_
beta_ = N - xn + beta_
rv = beta(alpha_, beta_)
観測データと事前分布のハイパーパラメータ$a,b$ から、事後分布のベータ分布の$\hat{a},\hat{b}$ を計算しています。
最後の行でパラメータ$\hat{a},\hat{b}$ の分布を求めています。
これが、今回の事後分布に対応しています。
学習結果は以下の通りです。(今回は$p=0.3$ として観測データを作りました。)
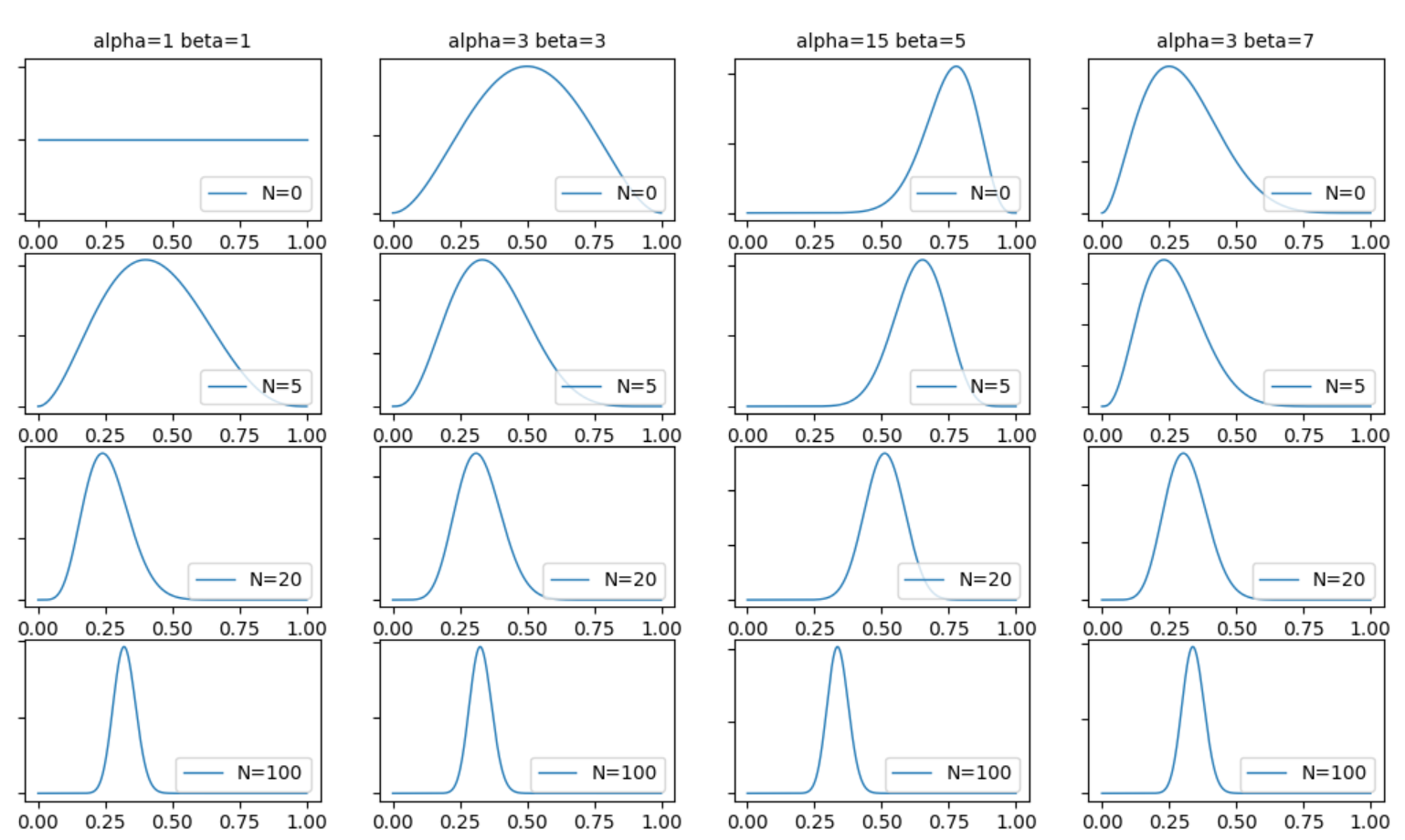
1行目は全く観測データが無い場合です。この場合、事前分布=事後分布です。
2行目から、観測データを元に事前分布が更新されています。
$N=5$ の場合、データ数が少ないので、事前分布のハイパーパラメータの影響がかなり大きいですが、$N=200$ になると、事前分布のハイパーパラメータに関わらず、全て同じような分布となります。
この事後分布は、観測データの生成時のパラメータ$p=0.3$ という情報は直接知っている訳ではありませんが、だいたい**$p=0.3$ 付近をピークに持つ分布**になっていることが分かります。
これは、観測データの特徴に合わせて事後分布が学習されていると言えます。
終わりに
今回は簡単なモデルを実際に書いてベイズ学習を復習しました。
MCMCなどを使うのはもう少し先になりそうですが、しっかり基礎を固めていきたいです。
※全体のコードはここに置きました。
