導入
過去の2回の記事では以下で定義されるロジスティック写像の軌道をグラフ反復法で描画し、パラメータごとのふるまいの違いを分岐図を使って見ました。
$$
f_a(x) = ax(1-x) \tag{1}
$$
今回はロジスティック写像における分岐図の構造を少し深掘りしていきます。とくに、こちらの記事で登場した軌道が吸い込まれる先の周期点の素周期が2,4,8と2倍ずつ大きくなっていくふるまいに注目します。このふるまいは周期倍分岐と呼ばれます。
今回はロジスティック写像において周期倍分岐が発生するパラメータ$a$を数値的に求めます。そして周期倍分岐が発生するパラメータに関して文献1や文献2で示された規則を数値的に確認します。
本記事の構成は以下のとおりです。最初にロジスティック写像における周期倍分岐の発生機構を解説します。次に周期倍分岐が発生するパラメータ$a$を数値的に求め、文献1の結果と整合することを確認します。最後に文献2で示されている周期倍分岐が発生するパラメータ間に成立する規則を数値的に確認します。
周期倍分岐の発生機構
不動点から2周期点への周期倍分岐が$a=3$を境にして発生することはこちらの記事で述べました。$a=3$付近における$f_a$と$f_a^2$のグラフを見てみましょう。$a=2.85,3,3.15$の場合の$f_a$と$f_a^2$のグラフを図1に示しました。黒い直線は$y=x$、赤い曲線は$y=f_a(x)$、青い曲線は$y=f_a^2(x)$のグラフをそれぞれ表しています。いずれのパラメータの場合においても$f_a$のグラフと$f_a^2$のグラフとは$y=x$上で交わっています。この交点は$f_a(x)=x$となる点なので$x=1-\frac{1}{a}$です。$f_a^2$のグラフは、$a=2.85$の場合は$y=x$上の交点に対して左下から右上に向かっており、$a=3.15$の場合は右下から左上に向かっています。この違いから$f_a^2$の$y=x$との交点$x=1-\frac{1}{a}$における導関数の値がパラメータを変えていったときに変化していく、つまり吸引的周期点から中立的周期点を経て反発的周期点に変化することがわかります。
図1. $f_a$と$f_a^2$のグラフ。上:$a=2.85$、中央:$a=3$、下:$a=3.15$



点$x=1-\frac{1}{a}$が吸引的周期点から反発的周期点に変化することを確かめましょう。
$f_a^2(x)$の導関数は以下になります。
$$
(f_a^2)'(x) = a^2(1-(2a+2)x + 6ax^2 - 4ax^3)
$$
したがって、点$x=1-\frac{1}{a}$では
$$
(f_a^2)'(1-1/a)=(a-2)^2
$$
となるため$a>3$では1より大きく、$a<3$では1より小さくなります。
図1に示したように$a>3$の場合、$f_a^2(x)$は$y=x$と新たな交点を2つ作ります。これらの点の一方を$x_1^{(2)}$、もう一方を$x_2^{(2)}$としましょう。ここでは$x_1^{(2)} < x_2^{(2)}$とします。
$x_1^{(2)}$と$x_2^{(2)}$は$f_a^2$の不動点ですがどちらも$f_a$のグラフ上にはないため、$f_a$にとっては不動点ではありません。つまり$x_1^{(2)}$と$x_2^{(2)}$とはどちらも1回写像では動きますが2回目の写像で戻ってくるような点です。このような点を素周期2の周期点と呼びました(参考:こちらの記事)。また、$f_a$は素周期2の周期点を2つしか持たないので、これらは互いに移り合う点です。すなわち
$$
f_a(x_1^{(2)}) = x_2^{(2)}, f_a(x_2^{(2)}) = x_1^{(2)}
$$
が成り立ちます。
$f_a^2$のグラフを見ると$x_1^{(2)}$と$x_2^{(2)}$では接線の傾きが1より小さくなるので、これらは吸引的な周期点です。こちらの記事で数値的に確認したように周囲の軌道が2周期点に吸い込まれていくふるまいが見られます。
周期倍分岐が発生するパラメータ
前の節で確認したパラメータ$a$を大きくしていくと吸引的不動点が反発的不動点になり、その周りに倍の周期の吸引的周期点が現れるふるまいを周期倍分岐と呼びます。ロジスティック写像において、周期倍分岐は$f_a^{2n}(n \in \mathbb{N})$の$n$を大きくしていった場合にも続いていきます。図2に$f_a^2$と$_a^4$のグラフを示しました。青い曲線が$f_a^2$のグラフで緑の曲線が$f_a^4$のグラフです。$x_1^{(2)}$と$x_2^{(2)}$のまわり(四角く囲った領域)において図1で見たふるまいが見られます。
図2. $f_a^2$と$f_a^4$のグラフ。$a=3.5$。

ロジスティック写像における周期倍分岐が発生するパラメータを数値的に求めます。周期倍分岐によって吸引的周期点は1周期、2周期、4周期...と変わっていきます。ここではちょうど周期倍分岐が発生して吸引的周期点の素周期が$2^p$になったときのパラメータを$a_p$と書くことにします。
本記事ではパラメータ$a_p$を次のようにして求めます。
- $p$を固定します。初期値は$p=0$とします
- パラメータ$a$を少しずつ変化させながら$f^{2^p}(x) - x$のグラフが$x$軸と交わる点を求めます。この点は写像$f^{2^p}(x)$の不動点になります
- 2.で求めた点における$f^{2^p}(x)$の微係数を計算します。パラメータ$a$が小さいうちは吸引的ですが、$a$を大きくしていくと反発的周期点に変化します。このときの$a$を$a_p$とします
- $p$の値を1大きくして2., 3.を繰り返します
上記の処理を実現するコードを下記に示しました。
from modules import one_dim_maps as maps
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['text.usetex'] = True
# f^N(x)のグラフを取得する
def get_graph(a, N, X0, F=maps.Logistic_Map):
X = np.copy(X0)
for _ in range(N):
X = F(a, X)
return X
# Yが0になるx座標の値を取得する
def get_zeros(X, Y):
index = np.where(Y[:-1] * Y[1:] < 0.)
a = (Y[:-1][index] - Y[1:][index])/(X[:-1][index] - X[1:][index])
b = Y[:-1][index] - a * X[:-1][index]
return -b / a
# f^Nの点x0における微係数を取得する
def get_differential_coefficient(a, x0, N, f=maps.logistic_map, dx=1e-6):
x1 = x0 - .5 * dx
x2 = x1 + dx
for _ in range(N):
x1 = f(a, x1)
x2 = f(a, x2)
return (x2 - x1) / dx
# 周期倍分岐が発生するパラメータaを取得する
def get_period_doubling_bifurcation_params(M, P, amin, amax = 4., da=1e-6):
X0 = np.linspace(0., 1., M, endpoint=False)
A = np.arange(amin, amax, da)
# 周期倍分岐が発生するパラメータaを格納するリスト
A_bifurcate = []
for p in range(0,P):
for j, a in enumerate(A):
# f^{2^p}のグラフを取得
Y = get_graph(a, 2**p, X0)
# f^{2^p} - xが0となる点=f^{2^p}の不動点を取得する
zeros = get_zeros(X0, Y - X0)
# f^{2^p}の不動点における微係数の絶対値を取得する
diff_coeffs = np.array([np.abs(get_differential_coefficient(a, x, 2**p)) for x in zeros])
if j == 0:
# 微係数の絶対値が1より小さい(吸引的)不動点の番号を取得する
index = np.where(diff_coeffs < 1.)
elif (diff_coeffs[index].size > 0) and (diff_coeffs[index] > 1.).all():
# 周期倍分岐が発生=吸引的不動点が反発的不動点に変わる
# 周期倍分岐が発生した直後のパラメータの値をA_bifurcateに格納する
A_bifurcate.append(a)
# 余計な計算を省くためにAを取り直す
A = np.arange(a, amax, da)
break
return A_bifurcate
A_bifurcate = get_period_doubling_bifurcation_params(10**5, 6, 2.999)
print(A_bifurcate)
モジュールone_dim_mapsはこちらの記事を参照してください。
メソッドget_zerosでは$f^{2^p}(x)$の$x$軸との交点を次のように近似して求めています。
- 区間$[0,1]$上の点列$\{ x_i\}(i=0,1,2,\dots)$の各点を$2^p$回写像して得られる点列を$\{ y_i\}(i=0,1,2,\dots)$とします
- $y_{i-1}y_i$が負になる$i$を取得します
- 点$(x_{i-1},y_{i-1})$と点$(x_{i},y_{i})$を結ぶ直線と$x$軸との交点を求めます
メソッドget_differential_coefficientでは中心差分法を使っています。中心差分法はPythonの数値計算モジュールであるSciPyでも使われている、よく知られた手法です(参考:scipy.misc.derivative)。
period_doubling_bifurcate_parameters.pyの実行結果は下記になります。
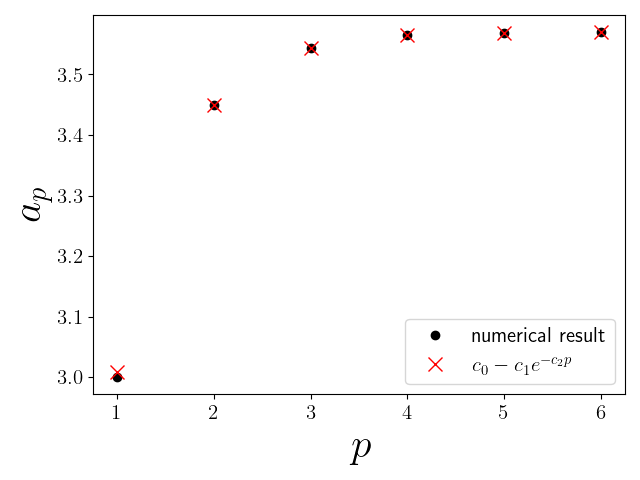
[3.00000100000014, 3.4494900000629687, 3.544091000076192, 3.5644080000790317, 3.56876000007964, 3.5696930000797704]
上記の結果を$p$に対してプロットしたものを図3に示しました。黒い点が数値的に得た$a_p$の結果です。赤いバツの点は下記の式(2)によって得た値です。
$$
a_p = c_0 - c_1e^{-c_2p} \tag{2}
$$
ここで$c0=3.56994567$、$c1=2.628$、$c2=1.543$としています。$a_p$が式(2)で与えられることは文献1において数値的に示されています。
図3. 周期倍分岐が発生するパラメータの数値的結果
本記事で示しているパラメータの値は決して最良というわけでも結果が収束しているわけでもないことに注意してください。各メソッドに渡すパラメータはちょうどいい値を選びます。またperiod_doubling_bifurcate_parameters.py自体も精度よくパラメータを求められるものではなく簡易的なものです。
ファイゲンバウム定数
period_doubling_bifurcate_parameters.pyのA_bifurcateの要素に対して以下の$d_p$を計算します。
$$
d_p = \frac{a_{p+1} - a_{p}}{a_{p+2} - a_{p+1}}
$$
period_doubling_bifurcate_parameters.pyの最下部に下記の処理を書き足します。
# 周期倍分岐が発生するパラメータ列{a_i}におけるd = (a_{i+1} - a_{i}) / (a_{i+2} - a_{i+1})を各iについて計算する
for p in range(len(A_bifurcate) - 2):
d_p = (A_bifurcate[p+1] - A_bifurcate[p])/(A_bifurcate[p+2] - A_bifurcate[p+1])
print(p, d_p)
実行結果は下記です。$p$を大きくするとおおよそ4.66...くらいの値になります。
0 4.75141911819114
1 4.656248461879215
2 4.668428308823529
3 4.664523043944266
$d_p$は$p$を大きくする極限である値に収束することが知られており
$$
d = \lim_{p \to \infty}d_p = 4.6692016091029\dots
$$
となります。この$d$はファイゲンバウム定数として知られています2。