カオス力学系の数値計算：ロジスティック写像の分岐を見る

導入

前回は以下で定義されるロジスティック写像の軌道をグラフ反復法でプロットしました。
$$
f_a(x) = ax(1-x) \tag{1}
$$

今回はロジスティック写像の性質について少し掘り下げていきます。とくに分岐と呼ばれる現象に注目します。分岐とは力学系が持つパラメータの変化に伴って力学系が質的に変化することを指します。本記事の最後ではロジスティック写像における分岐図や軌道図と呼ばれる図を数値的に描画します¹²³。ロジスティック写像における分岐図は複雑な構造を持つのですが、描画するにとどめます。その構造について詳しく書くと記事が非常に長くなってしまうためです。

本記事の構成は次のとおりです。最初の4つの節ではパラメータ$a$を下記の4通りの範囲に分けて軌道のふるまいを観察します。

• パラメータ範囲①：$0 < a \leq 1$
• パラメータ範囲②：$1 < a \leq 2$
• パラメータ範囲③：$2 < a \leq 3$
• パラメータ範囲④：$3 < a < 4$

お察しのとおり、これらの4つの範囲ごとに軌道のふるまいが違います。（最後だけちょっと大雑把な分け方であることを注意しておきます。）次に分岐図を描き、先の4つの節で観察した事象を分岐図であらためて観察します。

パラメータ範囲①

最初に$0 < a < 1$の場合の軌道を観察しましょう。図1に$a=0.5$および$a=0.9$の場合の軌道を示しました。どちらの場合においても軌道は$x=0$に吸い込まれていきます。

図1. ロジスティック写像の軌道をグラフ反復法でプロットしたもの(上：$a=0.5$、下：$a=0.9$)

軌道が吸い込まれていく点$x=0$が持つ特徴について説明します。点$x=0$は$0=f_a(0)$であるため写像によって動かない点です。このような写像によって動かない点は不動点または固定点と呼ばれます。明らかに直線$x_{n+1}=x_n$とグラフ$x_{n+1}=f(x_n)$との交点が不動点になります。パラメータが$0 < a < 1$の場合は$f_a(x_n)$と$x_{n+1}=x_n$とが$x_n=0$でのみ交わるので不動点はこれだけです。

周りの軌道が吸い込まれていく不動点は吸引的であると言います。吸引的不動点は沈点やアトラクターとも呼びます。もう少し厳密な定義を書くと写像$f$における不動点$x_{\rm{fix}}$が吸引的であるとは、写像の導関数について$\vert f'(x_{\rm{fix}})\vert < 1$が成り立つ場合のことを言います¹。なぜ$\vert f'(x_{\rm{fix}})\vert < 1$だと周りの軌道が吸引されるのかについてはたとえば文献¹や文献²を参照してください。標準的な理系大学で1年次に習う解析の知識で証明できます。

実際に不動点$x=0$が吸引的なのか計算して見ましょう。ロジスティック写像は$x$が$[0,1]$の範囲でなめらかなのでその範囲で微分できます。導関数は
$$
f_a'(x) = a(1 - 2x) \tag{2}
$$
ですから、$x=0$では$f_a'(0)=a$です。パラメータが$0 < a < 1$の場合は$\vert f_a'(0) \vert < 1$であるとわかります。

次に$a=1$の場合の軌道のふるまいを観察しましょう。図2に$a=1$の場合の軌道を示しました。パラメータが$0 < a < 1$と同じように軌道は$x=0$の方に向かっていきます。ですが式(2)からパラメータが$a=1$のときは$f_a'(0)=1$なので$x=0$は吸引的でありません。

図2. ロジスティック写像の軌道をグラフ反復法でプロットしたもの($a=1$)

一般に写像$f$における不動点$x_{\rm{fix}}$が$\vert f'(x_{\rm{fix}})\vert = 1$を満たすとき、その不動点は中立的であると言います¹。中立的不動点のまわりでは軌道は一方からは不動点に向かっていき、もう一方では不動点から離れていきます。ロジスティック写像では中立的不動点が写像の定義域の端点にいるので不動点に向かっていくふるまいのみが観察されます。パラメータを変えたときに中立的不動点が現れるような力学系ではしばしば分岐が発生します¹。

パラメータ範囲②

図3に$a=1.5$および$a=2$の場合の軌道を示しました。どちらの場合においても軌道は直線$x_{n+1}=x_n$とグラフ$x_{n+1}=f(x_n)$との$x=0$でない交点に吸い込まれていきます。前節で述べたように直線$x_{n+1}=x_n$とグラフ$x_{n+1}=f(x_n)$との$x=0$でない交点も不動点となります。

図3. ロジスティック写像の軌道をグラフ反復法でプロットしたもの(上：$a=1.5$、下：$a=2$)

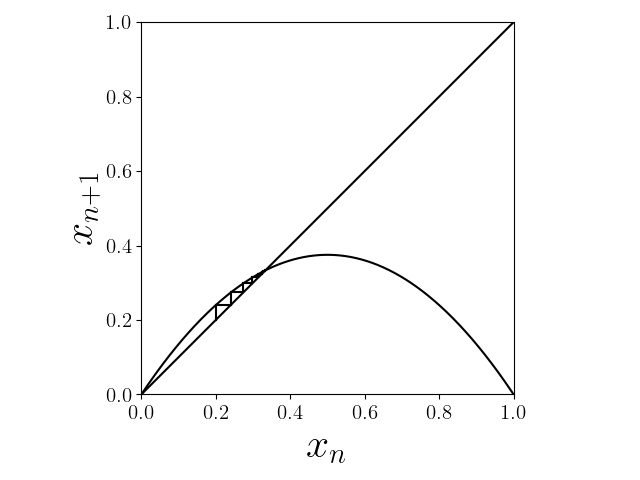
$x=0$でない方の不動点を以後$x^{(1)}$と書くことにします。$a>0$であるため簡単な2次方程式を解けば一般に
$$
x^{(1)} = 1 - \frac{1}{a} \tag{3}
$$
であることがわかります。

パラメータ$1 < a \leq 2$の場合の2つの不動点のそれぞれの特徴を調べていきましょう。式(2)から$x=0$において写像の導関数の値が今度は$\vert f_a'(0) \vert > 1$になります。このとき不動点は反発的であると言います。反発的不動点は源点やリペラーとも呼びます。反発的不動点のまわりでは軌道は不動点から離れていくふるまいをします。

前節で紹介した吸引的不動点と反発的不動点とを合わせて双曲的不動点と呼びます。厳密な言い方をすると、ある不動点$x^{(1)}$が双曲的不動点であるとはその点における写像の導関数が$\vert f_a'(x^{(1)}) \vert \neq 1$であることを言います。

式(2)および式(3)から不動点$x^{(1)}$における写像の導関数の値は
$$
f_a'(x^{(1)}) = 2 - a \tag{4}
$$
となるのでパラメータが$1 < a \leq 2$の場合は$\vert f_a'(x^{(1)}) \vert < 1$が成り立ちます。したがって、不動点$x^{(1)}$は吸引的であり、軌道は不動点$x^{(1)}$に吸い込まれていきます。

本節で見た軌道のふるまいと前節で見た軌道のふるまいを比べると中立的不動点が現れた$a=1$を境にガラッと変わっています。この変化は分岐のひとつの例です。

パラメータ範囲③

最初に$2 < a < 3$の場合の軌道を観察しましょう。図4に$a=2.7$および$a=2.9$の場合の軌道を示しました。不動点$x^{(1)}$における写像の導関数の値は$-1 < f_a'(x^{(1)}) < 0$となります。不動点$x=0$は反発的不動点のままですので吸引的不動点$x^{(1)}$にその周りの軌道は吸い込まれていきます。パラメータ$1 < a \leq 2$の場合と異なるのは不動点$x^{(1)}$の左側と右側を行ったり来たりしながら吸い込まれていく点です。

図4. ロジスティック写像の軌道をグラフ反復法でプロットしたもの(上：$a=2.7$、下：$a=2.9$)

次に$a=3$の場合の軌道を観察しましょう。図5に$a=3$の場合の軌道を示しました。不動点$x^{(1)}$の左側と右側を行ったり来たりしながら近付いていくふるまいが観察されます。ただ、$a=3$では不動点に吸収されていくスピードが遅く100回写像を繰り返した程度ではまだ行ったり来たりしている途中であることに注意してください。不動点$x^{(1)}$における写像の導関数の値は$f_a'(x^{(1)}) = -1$ですので不動点$x^{(1)}$は中立的です。前節で見たように$a=3$を境に分岐が発生します。

図5. ロジスティック写像の軌道をグラフ反復法でプロットしたもの($a=3$)

パラメータ範囲④

図6に$a=3.1$および$a=3.5$の場合の軌道を示しました。図では近づいていくまでのふるまいもプロットされているのが邪魔でわかりにくいですが、パラメータ$a=3.1$の場合、軌道はある程度長い時間が経過すると2点の間を行き来するようになります。パラメータ$a=3.5$の場合、軌道はある程度長い時間が経過すると4点の間を行き来するようになります。図6に示した軌道を時系列にしたもの図7に示しました。こちらの図の方が吸収された先が2点および4点であることがはっきりとわかります。

図6. ロジスティック写像の軌道をグラフ反復法でプロットしたもの(上：$a=3.1$、下：$a=3.5$)

図7. ロジスティック写像の軌道を時系列としてプロットしたもの(上：$a=3.1$、下：$a=3.5$)

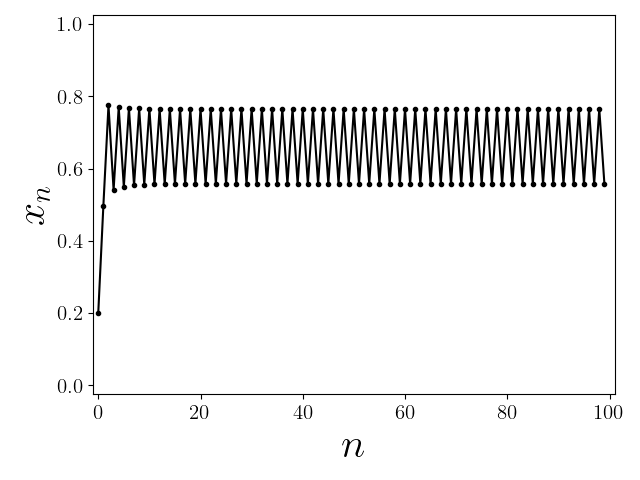
パラメータ$a=3.1$で行き来する2点はそれぞれ$f_a^2(x)$の不動点になっており、パラメータ$a=3.5$の4点はそれぞれ$f_a^3(x)$の不動点になっています。一般に写像を繰り返して元の位置に戻ってくるような点は周期点と呼ばれます。

一般に点$x^{(p)}$に対して写像$f$を繰り返したときに$n=1,2,\dots, p-1$では$f^{n}(x^{(p)})\neq x^{(p)}$で$f^{p}(x^{(p)})=x^{(p)}$となるとき、周期点$x^{(p)}$の素周期は$p$であるとか$p$周期の周期点とか言います。不動点は素周期1の周期点です。

パラメータ$a=3.1$と$a=3.5$とで軌道が吸い込まれていく周期点が変わりました。この先、$a$をさらに大きくすると吸い込まれていく周期点の周期がさらに2倍されていき、8周期、16周期…なっていきます。この変化もまた分岐の一例です。

分岐図

これまでの節で観察してきたようにロジスティック写像ではパラメータ$a$を変化させたときにある値を越えると分岐が発生しました。分岐が発生すると軌道が吸い込まれていく先や吸い込まれるまでのふるまいが変わりました。パラメータの変化幅をもっと小さくして細かくこのふるまいを見ていきましょう。パラメータのひとつひとつに対して軌道をグラフ反復法で描画して観察するのは手間なので分岐図を描きます。

分岐図は以下の手順で描画します。

1. パラメータ$a$を横軸にとり、縦軸に$x$をとります
2. パラメータ$a$を$0.0001$から始めて$0.0001$ずつ増加させながら、各パラメータごとに初期点$x_0=\frac{1}{2}$として、1000回写像します
3. 1000回写像したあと、もう1000回写像して通過した点をすべてプロットします

手順2で1000回写像しましたが1000回という値に特別な意味はなく、これくらい写像すれば周期点に吸い込まれたあとの状態が観察できるだろうという程度のものです。
初期点$x_0=\frac{1}{2}$とする理由については文献¹を参照してください。$x_0=\frac{1}{2}$でなくともほぼ同じ分岐図が描画できることを注意しておきます。

ロジスティック写像における分岐図を描画するコードは以下です。

bifurcation_diagram.py

import one_dim_maps as maps
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
import copy
mpl.rcParams['text.usetex'] = True

def get_orbit(f, a, x0, N):
    orbit = np.ones(N) * np.nan
    x = copy.deepcopy(x0)
    for i in range(N):
        orbit[i] = x
        x = f(a, x)
    return orbit

def plot_bifurcation_diagram(amin, amax, x0, N_trans, N, da = 1e-4):
    fig = plt.figure()
    ax = fig.add_subplot(111)

    A = np.arange(amin, amax, da)

    for a in A:
        a_s = np.ones(N) * a
        orbit = get_orbit(maps.logistic_map, a, x0, N_trans + N)
        ax.plot(a_s, orbit[N_trans:N_trans + N], ',', color='k')
    
    ax.tick_params(labelsize=15)
    ax.set_xlabel("$a$", fontsize = 30)
    ax.set_ylabel("$x$", fontsize = 30)
    ax.set_ylim(-0.05, 1.05)
    ax.set_ylim(0.3, 0.4)
    plt.tight_layout()
    plt.show()

plot_bifurcation_diagram(1e-4, 4., 0.5, 10**3, 10**3)

モジュールone_dim_maps.pyについてはこちらの記事を参照してください。

図8にロジスティック写像の分岐図を$a=3.5$まで示しました。$a=1$で$x=0$から$x = x^{(1)} \neq 0$へと吸い込まれる先が切り替わる分岐が見られます。$a=3$では不動点から2周期の周期点に吸い込まれる先が切り替わる分岐が、さらに$a=3$と$a=3.5$の間で4周期の周期点に切り替わる分岐が見られます。

図8. ロジスティック写像の分岐図($0.0001 \leq a \leq 3.5$)

さらに$a$を大きくしていき、$a=4$までの分岐図と$3.55 \leq a \leq 3.65$の部分の拡大図を図9に示しました。まず前者の図では黒く塗りつぶしたような部分とポッカリと空いた空白が観察できます。ポッカリと空いた空白は窓と呼ばれます¹²。後者の拡大図では窓にはさまざまな大きさのものが複数あるとわかります。また空白と空白の間の塗りつぶされているように見えた部分にも濃淡があるとわかります。濃淡もランダムにできているのではなく、なんらかの構造がありそうです。これらの構造については次回以降に説明したいと思います。

図9. ロジスティック写像の分岐図($0.0001 \leq a \leq 4$)

1. R. L. Devaney, 『新訂版 カオス力学系入門 第2版』, 共立出版 (2003). ↩ ↩² ↩³ ↩⁴ ↩⁵ ↩⁶ ↩⁷

2. M. W. Hirsch, S. Smale and R. L. Devaney, 『力学系入門 原著第2版』, 共立出版 (2007). ↩ ↩² ↩³

3. 小室 元政, 『新版 基礎からの力学系』, サイエンス社 (2005). ↩