Pythonで画像のエッジ検出と直線検出をする

1.概要

みんな大好き大乱闘スマッシュブラザーズ(以下スマブラ)！！
私事ながら，スマブラ配信をしています．チャンネル登録お願いします！
スマブラ×機械学習でなんかできないかなー，と思っていたところこんな記事を発見しました．
画像認識でスマブラの戦績を自動で作成するツールを作ろう
最終的に何を作るかは置いといて，面白そうだしとりあえずやってみよう！

前回，Pythonで指定した範囲のスクリーンショットを撮ることができました．
今回の目標は，前回撮った画像からエッジ検出と直線検出をすることです．
こんな画像から，

エッジを検出して，

画像内の直線を検出したい！

2.本編

今回はこんな流れで進めていきます．

2-1.画像をグレースケールに変換

前回撮ったスクリーンショットをグレースケールに変換します．
画像の1ピクセルに含まれる情報は，RGBなら256×3，グレースケールなら256×1になります．つまり，扱う情報量が$\frac{1}{3}$に減るため，処理時間の短縮につながります．

前回撮ったスクリーンショットはImage型ですが，OpenCVではnumpyのndarrayで画像を扱います．
ndarrayにしてからグレースケールに変換すると，後述のRGBとBGRの関係で不都合があります．ということで，今回はImage型のままグレースケールに変換，その後ndarrayに変換という順番でやっていきます．
グレースケールへの変換はこの記事，ndarrayへの変換はこの記事を参考にしました．

import pyautogui

# im: 前回pyautoguiで撮ったスクリーンショット
im = pyautogui.screenshot("screenshot.png")
# Image型のまま画像をグレースケールに変換
im_gray = im.convert("L")
# OpenCVで扱えるようにImage型をndarrayに変換
im_gray = np.array(im_gray, dtype=np.uint8)
# ちゃんとグレースケールになっているか確認
cv2.imwrite("gray", im_gray)

この画像が，

こうなりました．

ちゃんとできてそうですね．いい感じ！

今回はグレースケールの画像を扱うので関係ありませんが，OpenCVではカラー画像をRGBではなくBGRで扱うらしいです．カラー画像を使う際には注意しないといけませんね．
ちょっと調べてみましたが，明確な理由はあまりなさそうでした．なんでですかね？？

2-2.画像のリサイズ

次回，一定の位置にあるエッジや直線を用いて，対戦開始・終了タイミングの検知をするつもりなので，画像のサイズを整えておきます．
画像のリサイズはこの記事を参考にしました．

ここからはOpenCVを使います．
まず，OpenCVをインストール！

$ pip install opencv-python

インストールできたらOpenCVに用意されているresize関数を使うだけ！

import cv2

# グレースケール画像を，幅1024，高さ576にリサイズ
im_resize = cv2.resize(im_gray, dsize=(1024, 576))

今回は16:9にしたかったので適当に1024×576にしましたが，もう少し小さくても問題なく検知できると思います．というか，小さくした方がこの後の処理が早くなっていいと思います．知らんけど．

2-3.Canny法でエッジ検出

Canny法ってやつを使えばエッジの検出ができるらしいです．(内容ちゃんと理解できてないので，今度ちゃんと理解してから別で記事書きます)
OpenCVに用意されている関数があるので，それを使います．
Canny法の全般的な内容はこの記事，パラメータの調整はこの記事を参考にしました．

import cv2

# Canny法でエッジ検出
im_edges = cv2.Canny(im_resize, 130, 285, L2gradient=True)
# 確認
cv2.imwrite("edges", im_edges)

この画像が，

こうなりました．

画面上部の並行な直線を検知できそうですね！

cv2.Cannyの引数についての詳細は以下に示します．

引数	詳細
第一引数	エッジを検出したい画像(ndarray)
第二引数	エッジに隣接する場所がエッジかどうかを判定する閾値
第三引数	そもそもエッジかどうかを判定する閾値
第四引数	Trueとすることでエッジ強度の計算が正確になる

第三引数の値を小さくするとエッジと判定される場所が増え，第二引数の値を小さくするとそのエッジから線が伸びていくようなイメージで調整します．
今回は第二引数が130，第三引数が285でいい感じになりました．
第四引数はデフォルトではFalseとなっています．Falseの場合にはL1ノルムで勾配が計算されるので計算時間はFalseの方が早いと思います．

2-4.Hough変換で直線検出

Hough変換とやらで直線検出ができるらしいです．(これもちゃんと理解してから別で記事書きます)
Hough変換では，$x,y$で表される直交座標系を$\rho,\theta$で表される極座標系に変換して扱います．
これは，直交座標系では扱いにくい"$x$軸に垂直な線"を扱いやすくするためらしいです．(パラメータが無限大に発散しない)
これも難しい話を抜きにすればOpenCVの用意されている関数を使えば簡単に実装できます．
OpenCV最強！
Hough変換の全般的な内容はこの記事，検出した直線の描画はこの記事，描画に使用したline関数についてはこの記事を参考にしました．

import cv2

# Hough変換で直線を検出
im_lines = cv2.HoughLines(im_edges, rho=1, theta=np.pi/180, threshold=200)
# 検出された直線を確認
print(im_lines)

第四引数のthresholdは直線上にどれほどのエッジがあれば直線と判定するかの閾値です．値を大きくすると直線と判定されるのに，より多くのエッジが必要になります．今回は調整の結果，200でいい感じになりました．

[[[ 82.          1.5358897]]
 [[100.          1.5358897]]]

今回の場合，$\rho=82, \theta=1.5358897$，$\rho=100, \theta=1.5358897$の2本の直線が検出されました．
ここで，$\rho$とか$\theta$とかなんぞや？って人のために極座標系について少し説明します．

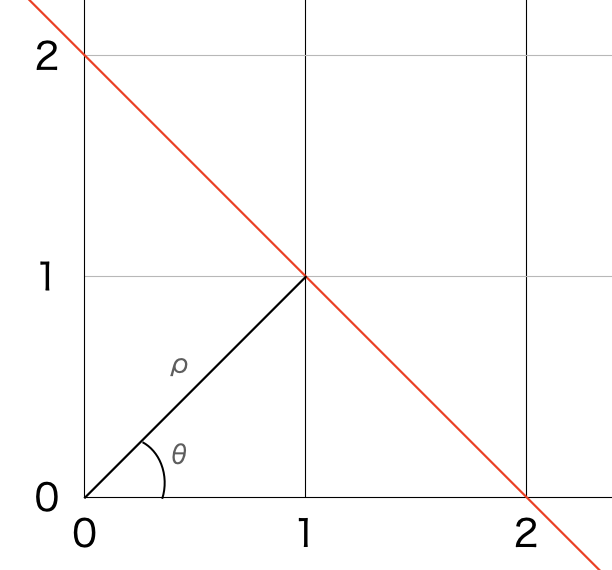
極座標系では原点からの距離$\rho$と，角度$\theta$を用いて座標を表現します．
例えば，直交座標系の$(1,1)$は，原点からの距離が$\sqrt{2}$，角度が$\pi/4$なので，極座標系で$(\sqrt{2},\pi/4)$と表されます．
原点と$(\sqrt{2},\pi/4)$を通る直線に垂直な直線で，$(\sqrt{2},\pi/4)$を通る直線は上の図の赤い直線のように一意に決まります．これは$(\sqrt{2},\pi/4)$以外でも同様で，原点以外であれば，$\rho,\theta$から直線が一意に決まります．
このように表された直線が上の実行結果で示されたものです．

それでは，検出された2本の直線を画像に描画し，確認します．
描画にはOpenCVのline関数を使用しました．
line関数の引数の詳細は以下の通りです．

引数	詳細
第一引数	線分を描画する画像
第二引数	線分の始点
第三引数	線分の終点
第四引数	線分の色(BGR)
第五引数	線分の太さ

import cv2
import numpy as np

def draw_line(img, theta, rho):
    h, w = img.shape[:2]
    # 直線が垂直のとき
    if np.isclose(np.sin(theta), 0):
        x1, y1 = rho, 0
        x2, y2 = rho, h
    # 直線が垂直じゃないとき
    else:
        # 直線の式を式変形すればcalc_yの式がもとまる(解説を後述します)．
        calc_y = lambda x: rho / np.sin(theta) - x * np.cos(theta) / np.sin(theta)
        x1, y1 = 0, calc_y(0)
        x2, y2 = w, calc_y(w)
    x1, y1, x2, y2 = map(int, [x1, y1, x2, y2])
    # 直線を描画
    cv2.line(img, (x1, y1), (x2, y2), (0, 255, 0), 2)

# screenshot.pngをカラー画像で読み込んでリサイズ
im_straight = cv2.resize(cv2.imread("screenshot.png"), dsize=(1024, 576))
# 直線が検出されている場合だけ描画する
if not im_lines is None:
    # 各直線を描画
    for line in im_lines:
        rho, theta = line[0]
        draw_line(im_straight, theta, rho)
    # 直線が描画された画像を書き出し
    cv2.imwrite("straight.png", im_straight)

検出された直線を描画した結果はこんな感じ．

しっかり画面上部の並行な直線が検出されていますね．
対戦開始のタイミングを検知できそうです！

上のコードのcalc_yの部分だけ少し分かりにくいので解説します．難しい内容ではありませんが，面倒くさい人は読み飛ばしてください．

calc_yの詳しい解説

calc_yは極座標系の$\rho,\theta$を使って，直交座標系の直線を表し，$x$座標が与えられたときそれに対応する$y$座標を計算する式です．
つまり，下の図の赤い直線の式を$y=ax+b$の形で表すとき，傾き$a$，切片$b$を$\rho,\theta$で表したものです．

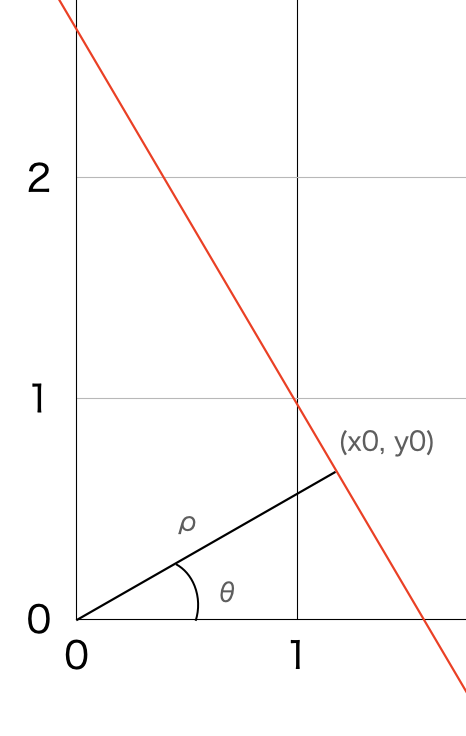
まず，直交座標系の$x0,y0$は$\rho,\theta$を使って，$x0=\rho\cos\theta,y0=\rho\sin\theta$のように表すことができます．これは$\sin,\cos$の定義から自明です．
次に，赤い直線の傾き$a$をもとめます．
原点と$(x0,y0)$を通る直線の傾きは$y0/x0$と表すことができ，直交する直線の傾きの積は$-1$になるため，

\begin{align}
\frac{y0}{x0}\times a&=-1 \\
a&=-\frac{x0}{y0} \\
a&=-\frac{\rho\cos\theta}{\rho\sin\theta} \\
a&=\frac{\cos\theta}{\sin\theta} 
\end{align}

となります．これで傾き$a$がもとまりました．
次は直線の式 $y=ax+b$ に$x0,y0,a$を代入することで切片$b$をもとめます．
$\sin^{2}\theta+\cos^{2}\theta=1$であることに注意すると，

\begin{align}
y&=ax+b \\
y0&=-\frac{\cos\theta}{\sin\theta}x0+b \\
\rho\sin\theta &= -\frac{\cos\theta}{\sin\theta}\rho\cos\theta +b \\
b&=\frac{\rho\sin^{2}\theta}{\sin\theta}+\frac{\rho\cos^{2}\theta}{\sin\theta} \\
b&=\frac{\rho\left(\sin^{2}\theta+\cos^{2}\theta\right)}{\sin\theta} \\
b&=\frac{\rho}{\sin\theta}
\end{align}

となります．これで傾き$a$と切片$b$がもとまったので，直線の式がわかりました．

\begin{align}
y&=ax+b \\
y&=-\frac{\cos\theta}{\sin\theta}x+\frac{\rho}{\sin\theta}
\end{align}

この式がcalc_yの正体です．

3.まとめ

• 前回やったこと
  • マウスでクリックした位置を取得
  • クリックで指定した範囲のスクリーンショットを撮影
• 今回やったこと
  • 画像をグレースケールに変換
  • 画像のリサイズ
  • Canny法でエッジ検出
  • Hough変換で直線検出
• 次回やること
  • 検出した直線から対戦開始のタイミングを検知
  • グレースケール画像からテンプレートマッチングで対戦終了のタイミングを検知

4.終わりに

前回から1週間ぐらいかかってしまいました．
年内に完成させるつもりだったんですけど，厳しそうですね．．
それと，Canny法，Hough変換についてはちゃんと理解して，また別で記事を書きます！

参考文献

画像認識でスマブラの戦績を自動で作成するツールを作ろう
Python でグレースケール(grayscale)化
Pillow ↔ OpenCV 変換
OpenCV – resize で画像をリサイズする方法
Canny法によるエッジ検出
cv2.Canny(): Canny法によるエッジ検出の調整をいい感じにする
ハフ変換による直線検出
OpenCVで直線の検出
【OpenCV】cv2.line関数の使い方【線分を描画する】