用語
| 用語 | リンク |
|---|---|
| 相関係数 | https://qiita.com/kenmero/items/1265d8c89c67650e4c13#%E7%9B%B8%E9%96%A2%E9%96%A2%E6%95%B0 |
| 箱ひげ図 |
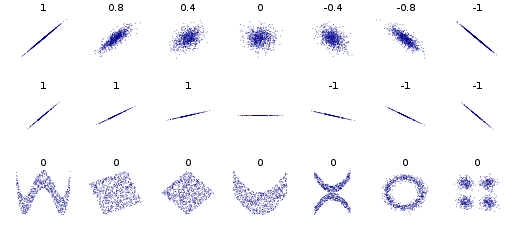
相関係数
相関係数(ピアソン相関)の考え方は、2つの要素(確率変数)の「線形関係」を見つけるものである。
※線形とは、変数と変数の関係が直線的である関係を表す言葉である。(= xとyの関係が1次関数)
相関係数には、原則や単位は存在せずに、
-1から1の間に実数値をとります。
1に近いときは2つの要素にプラスの相関があるといい、
-1に近いときにはマイナスの相関があるといいます。
※プラスの相関・・・片方が上がれば、もう片方も上がる
マイナスの相関・・片方が上がれば、もう片方は下がる
0にちかいときは相関は弱い(ない)と判断されます。
また、相関関係は2つの関係が線形の場合に効果を発揮するものであるため、
非線形(2次曲線など、、)には効果はでず、相関がない(0に近似した値)となります。
※wikiから抜粋
https://en.wikipedia.org/wiki/Pearson_correlation_coefficient
参考サイト:
http://tomoshige-n.hatenablog.com/entry/2014/08/06/035001
https://qiita.com/te20/items/e91faee8f9eb9b1a869c
箱ひげ図
データの中央値(平均値)の個所をパット見で判断しやくした図。
箱ひげ図では全体の25%(第1四分位数)、50%(第2四分位数)、75%(第3四分位数)の値を特定し図に表現する。
25%から75%の間の値が集中しているデータであると判断する。
以下の場合の箱ひげ図を例に説明
7人に数学のテスト結果を箱ひげ図で洗わす。
1点 3点 4点 5点 6点 6点 10点
手順
1.最小値と最大値を特定する。
最小値:1点
最大値:10点
2.中央値を特定する
中央値:5点(第2四分位数:50%の値)
3.2から最少値の間の中央値を特定する
中央値(左):3点(第一四分位数:25%の値)
4.2から最大値の間の中央値を特定する
中央値(右):6点(第三四分位数:75%の値)