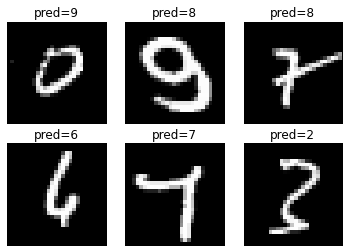【機械学習】k-nearest neighbor method(k最近傍法)を自力でpythonで書いて、手書き数字の認識をする

前回はテンプレートマッチング法を用いて手書き数字に識別を行いましたが今回は手法を変えてk最近傍法(k-nearest neighbor method)を使おうと思います。

k最近傍法の概要

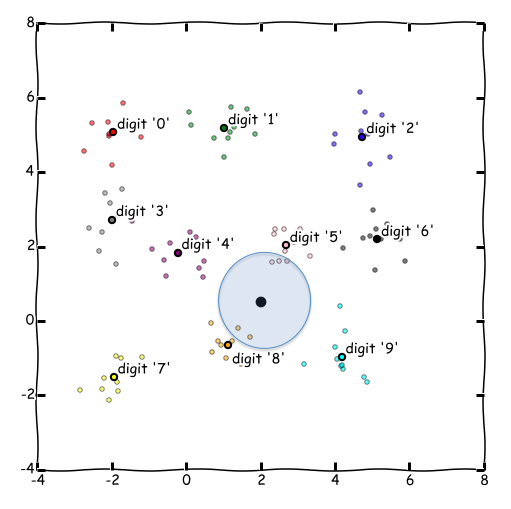
まずは手法の概要ですが、下記の図のように黒い点を識別対象データとすると、そこからの距離が近いk個の教師データを探し出し、多数決で一番多いラベルを推測値として選択します。この例の場合、"5"が3個、"8"が2個なので、"5"が推測値として採用されることになります。
特徴としては、教師あり分析であることと、計算のためにすべてのデータを計算に利用するのでメモリサイズと計算量を食うところでしょうか。”近い”の概念として普通の距離（ユークリッド距離）、マハラノビスの距離（分散を利用する）等幾つかありますが、今回は普通の距離を使います。

##実装する##

さっそくPythonで書いていきます。
まずは必要なライブラリ類のインポートです。sklearnなど機械学習自体のライブラリは今回使いません。（自力なので）

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
from collections import defaultdict

TrainDataSetというクラスを定義します。教師データなので結果のラベル（手書き数字の数字）、ピクセルデータの２つを保持して、特定の要素のみ取り出すなど、必要なデータを簡単に取り出せるようにしています。

class TrainDataSet():
    def __init__(self, data):
        data = np.array(data)
        
        self.labels = data[:,0]
        self.data_set = data[:,1:]
        
    def __repr__(self):
        ret  = repr(self.labels) + "\n"
        ret += repr(self.data_set)
        return ret
        
    def get_data_num(self):
        return self.labels.size
        
    def get_labels(self, *args):
        if args is None:
            return self.labels
        else:
            return self.labels[args[0]]
    def get_data_set(self):
        return self.data_set
        
    def get_data_set_partial(self, *args):
        if args is None:
            return self.data_set
        else:
            return self.data_set[args[0]]
    def get_label(self, i):
        return self.labels[i]
    def get_data(self, i):
        return self.data_set[i,:]
    def get_data(self,i, j):
        return self.data_set[i][j]

次にデータを読み込みます。試してみたい方は下記からデータのダウンロードが出来ます。
train.csv ... 教師データ(42000個)
test_small.csv ... 識別対象データ(200個)

size = 28
master_data= np.loadtxt('train_master.csv',delimiter=',',skiprows=1)
test_data= np.loadtxt('test_small.csv',delimiter=',',skiprows=1)

train_data_set = TrainDataSet(master_data)

また、近傍k個の結果を集計して各数字ラベル毎に何個のデータがあるかをリストにして出力する関数を定義しています。

def get_list_sorted_by_val(k_result, k_dist):
    result_dict = defaultdict(int)
    distance_dict = defaultdict(float)
    
    # 数字ラベルごとに集計
    for i in k_result:
        result_dict[i] += 1
    
    # 数字ラベルごとに距離の合計を集計
    for i in range(len(k_dist)):
        distance_dict[k_result[i]] += k_dist[i]
    
    # 辞書型からリストに変換（ソートするため）
    result_list = []
    order = 0
    for key, val in result_dict.items():
        order += 1
        result_list.append([key, val, distance_dict[key]])
    
    # ndarray型に変換
    result_list = np.array(result_list) 

    return result_list

さて諸々準備が完了し、ここから識別処理が始まります。今回近傍としてk=5つのデータを選びます。

k = 5
predicted_list = []    # 数字ラベルの予測値
k_result_list  = []    # k個の近傍リスト
k_distances_list = []  # k個の数字と識別対象データとの距離リスト

# execute k-nearest neighbor method
for i in range(len(test_data)):
  
    # 識別対象データと教師データの差分をとる
    diff_data = np.tile(test_data[i], (train_data_set.get_data_num(),1)) - train_data_set.get_data_set()
    
    sq_data   = diff_data ** 2       # 各要素を2乗して符号を消す
    sum_data  = sq_data.sum(axis=1)  # それぞれのベクトル要素を足し合わせる
    distances = sum_data ** 0.5      # ルートをとって距離とする
    ind = distances.argsort()        # 距離の短い順にソートしてその添え字を取り出す
    k_result = train_data_set.get_labels(ind[0:k]) # 近いものからk個取り出す
    k_dist   = distances[ind[0:k]]   # 距離情報もk個取り出す
    
    k_distances_list.append(k_dist)
    k_result_list.append(k_result)
    
    # k個のデータから数字ラベルで集約した、(数字ラベル, 個数, 距離)のリストを生成
    result_list = get_list_sorted_by_val(k_result, k_dist)
    candidate = result_list[result_list[:,1].argsort()[::-1]]

    counter = 0
    min = 0
    label_top = 0
    
    # もっとも数の多い数字ラベルが複数あったらその中で合計距離の小さい方を選択
    result_dict = {}
    for d in candidate:
        if d[1] in result_dict:
            result_dict[d[1]] += [(d[0], d[2])]
        else:
            result_dict[d[1]] =  [(d[0], d[2])]

    for d in result_dict[np.max(result_dict.keys())]:
        if counter == 0:
            label_top = d[0]
            min = d[1]
        else:
            if d[1] < min:
                label_top = d[0]
                min = d[1]
        counter += 1
                
    # 結果をリストに詰める
    predicted_list.append(label_top)

結果を表示します。

# disp calc result
print "[Predicted Data List]"
for i in range(len(predicted_list)):
    print ("%d" % i) + "\t" + str(predicted_list[i])

print "[Detail Predicted Data List]"
print "index k units of neighbors, distances for every k units"
for i in range(len(k_result_list)):
    print ("%d" % i) + "\t" + str(k_result_list[i]) + "\t" + str(k_distances_list[i])

出力された結果ファイルはココに、正解と識別した予測値を照らし合わせた結果はココにあります。
今回はk最近傍法を使って200個の識別してみましたが、識別率が97%(194/200)と格段に上がりました！これくらい識別が良いと実用的になってくるんじゃないでしょうか。前回行ったテンプレートマッチングの場合、80%でしたからこれと比べてもかなりいいですね。

Failデータの分析

下記の6つのデータがfailしたものですが、やはり目視で見ても厄介そうなデータですね。下段1つ目のデータなんで目視でも6か4か微妙です・・・そういったそもそもの手書き数字が微妙なもの以外はk最近傍法ではほとんど識別できていると言えそうです。

counter = 0
for d, num in zip(test_data, [3,76,128,132,147,165]):
    counter += 1
    X, Y = np.meshgrid(range(size),range(size))
    Z = test_data[num].reshape(size,size)
    Z = Z[::-1,:]
    flat_Z = Z.flatten()
    plot_digits(X, Y, Z, 2, 3, counter, "pred=%d" % predicted_list[num])

failデータの詳細

index	label	pred	k-nearest digits	remarks
3	0	9	[ 0. 9. 9. 9. 2.]	最近傍は0なのに・・・おしい。
76	9	8	[ 8. 8. 9. 8. 3.]	9も１個は入っているが・・・
128	7	1	[ 8. 1. 7. 8. 1.]	7に余計な線入れないで・・・
132	4???	6	[ 6. 6. 6. 6. 6.]	これ、4か6か目視でも微妙
147	4	7	[ 7. 7. 7. 7. 7.]	これ、もしかして7であってるのかな
165	3	2	[ 3. 2. 2. 2. 3.]	3もいい線いっていたけど・・・