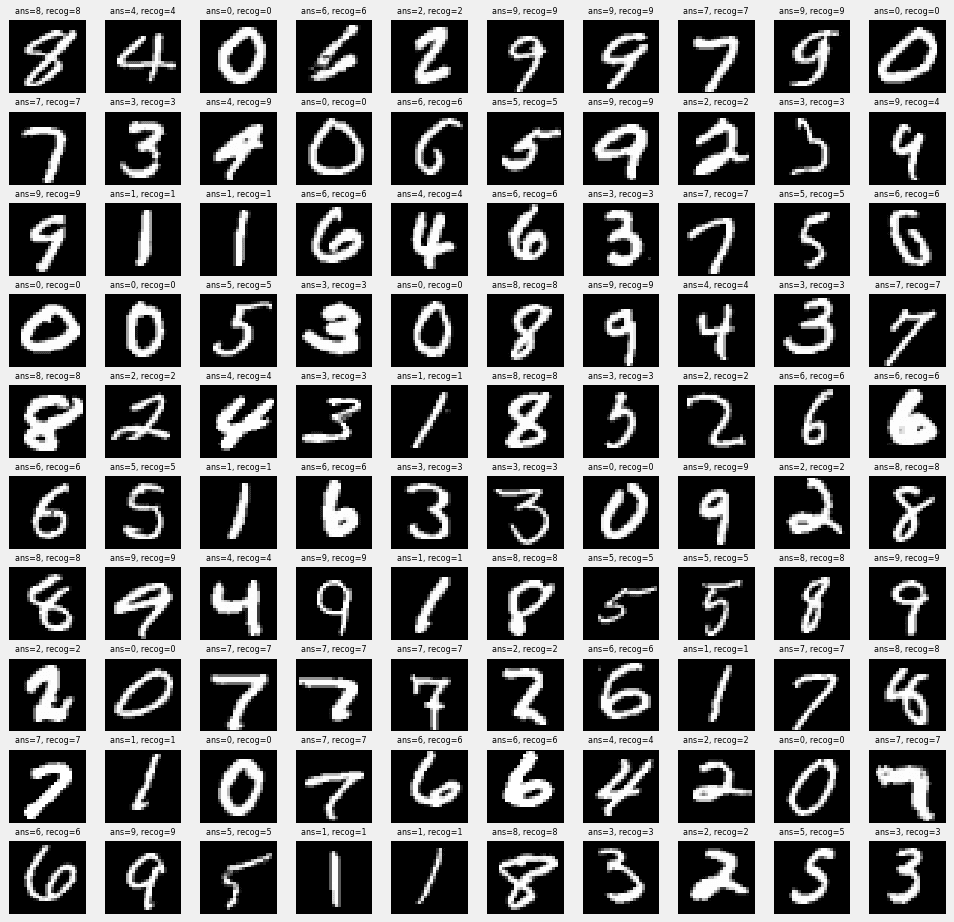【機械学習】ディープラーニング フレームワークChainerを試しながら解説してみる。

今話題のDeep Learning(深層学習)フレームワーク、Chainerに手書き文字の判別を行うサンプルコードがあります。こちらを使って内容を少し解説する記事を書いてみたいと思います。

(本記事のコードの全文をGitHubにアップしました。[PC推奨])

とにかく、インストールがすごく簡単かつ、Pythonが書ければすぐに使うことができておすすめです！
Pythonに閉じてコードが書けるのもすごくいいですよね。

こんな感じのニューラルネットワークモデルを試してみる、という記事です。

主要な情報はこちらにあります。
Chainerのメインサイト
ChainerのGitHubリポジトリ
Chainerのチュートリアルとリファレンス

#1. インストール#

まずは何はともあれインストールです。ChainerのGitHubに記載の"Requirements" ( https://github.com/pfnet/chainer#requirements )を参考に必要なソフト、ライブラリをインストールした上で

pip install chainer

を実行します。
これだけでインストールできちゃいます。超簡単！CaffeをMacにインストールしようとした時はかなり苦戦しましたが、嘘のようです

もし、インストールに詰まったらcvl-robotさんの「DeepLearningライブラリのChainerがすごい、らしい」という記事が詳しく必要なライブラリ等のインストールについて記載してくれていて便利です。

#2.サンプルコードの入手#
GitHubの下記ディレクトリにおなじみMNISTの手書き文字を判別する、というサンプルがありますので、これを題材としたいと思います。これをChainerの順伝播型ニューラルネットワークでClassificationしてみる、という試みです。
https://github.com/pfnet/chainer/tree/master/examples/mnist
　　┗ train_mnist.py

このコードにコメントを加えたり、一部途中のフローをグラフで表示してイメージをつけたりしながら見ていきたいと思います。

#3.サンプルコードを見ていく#
今回、手持ちのMacbook Air(OS X ver10.10.2)での動作確認をしながら書いていますので、環境によっては差分があるかもしれませんが、そこはよしなに見てもらえればと思っています。また、こういった環境のためGPUでの計算は行わずCPUのみとなりますのでGPU関連のコードは省略して記載します。

##3-1.準備##

まず最初に必要なライブラリ群のインポートです。

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import fetch_mldata
from chainer import cuda, Variable, FunctionSet, optimizers
import chainer.functions  as F
import sys

plt.style.use('ggplot')

次に各種パラメーターの定義・設定を行います。

# 確率的勾配降下法で学習させる際の１回分のバッチサイズ
batchsize = 100

# 学習の繰り返し回数
n_epoch   = 20

# 中間層の数
n_units   = 1000

Scikit LearnをつかってMNISTの手書き数字データをダウンロードします。

# MNISTの手書き数字データのダウンロード
# #HOME/scikit_learn_data/mldata/mnist-original.mat にキャッシュされる
print 'fetch MNIST dataset'
mnist = fetch_mldata('MNIST original')
# mnist.data : 70,000件の784次元ベクトルデータ
mnist.data   = mnist.data.astype(np.float32)
mnist.data  /= 255     # 0-1のデータに変換

# mnist.target : 正解データ（教師データ）
mnist.target = mnist.target.astype(np.int32)

3つくらい取り出して描画してみます。

# 手書き数字データを描画する関数
def draw_digit(data):
    size = 28
    plt.figure(figsize=(2.5, 3))

    X, Y = np.meshgrid(range(size),range(size))
    Z = data.reshape(size,size)   # convert from vector to 28x28 matrix
    Z = Z[::-1,:]             # flip vertical
    plt.xlim(0,27)
    plt.ylim(0,27)
    plt.pcolor(X, Y, Z)
    plt.gray()
    plt.tick_params(labelbottom="off")
    plt.tick_params(labelleft="off")

    plt.show()

draw_digit(mnist.data[5])
draw_digit(mnist.data[12345])
draw_digit(mnist.data[33456])

28x28, 784次元ベクトルのこんなデータですね。

データセットを学習用データ検証用データに分割します。

# 学習用データを N個、検証用データを残りの個数と設定
N = 60000
x_train, x_test = np.split(mnist.data,   [N])
y_train, y_test = np.split(mnist.target, [N])
N_test = y_test.size

##3.2 モデルの定義##

いよいよモデルの定義です。ここからが本番ですね。Chainerのクラスや関数を使います。

# Prepare multi-layer perceptron model
# 多層パーセプトロンモデルの設定
# 入力 784次元、出力 10次元
model = FunctionSet(l1=F.Linear(784, n_units),
                    l2=F.Linear(n_units, n_units),
                    l3=F.Linear(n_units, 10))

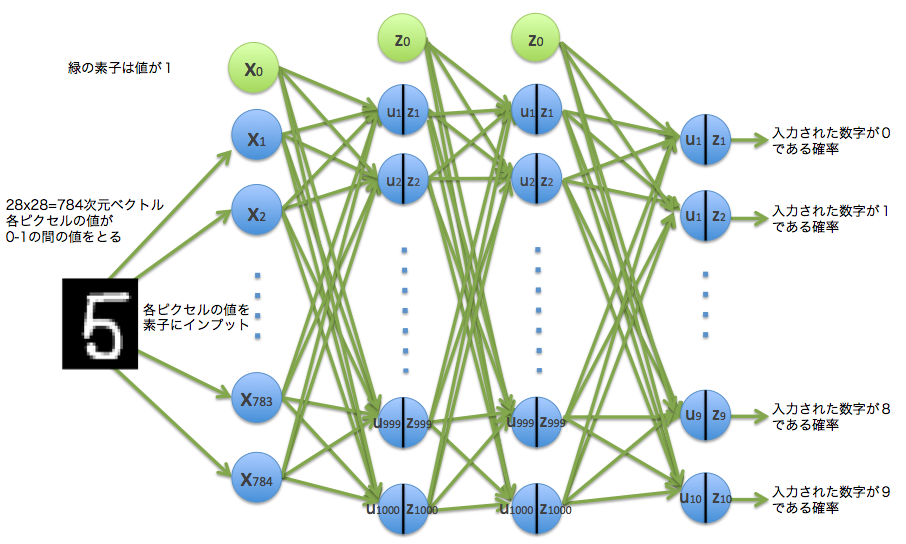
入力の手書き数字のデータが784次元ベクトルなので、入力素子は784個になります。今回中間層はn_unitsで1000と指定しています。出力は、数字を識別するので10個になります。下記がこのモデルのイメージです。

順伝播の構造が下記のforward()関数で定義されます。

# Neural net architecture
# ニューラルネットの構造
def forward(x_data, y_data, train=True):
    x, t = Variable(x_data), Variable(y_data)
    h1 = F.dropout(F.relu(model.l1(x)),  train=train)
    h2 = F.dropout(F.relu(model.l2(h1)), train=train)
    y  = model.l3(h2)
    # 多クラス分類なので誤差関数としてソフトマックス関数の
    # 交差エントロピー関数を用いて、誤差を導出
    return F.softmax_cross_entropy(y, t), F.accuracy(y, t)

ここで各関数等を説明したいと思います。
Chainerのお作法で、データは配列からChainerのVariableという型（クラス）のオブジェクトに変換して使います。

x, t = Variable(x_data), Variable(y_data)

活性化関数はシグモイド関数ではなく、F.relu()関数が使われています。

F.relu(model.l1(x))

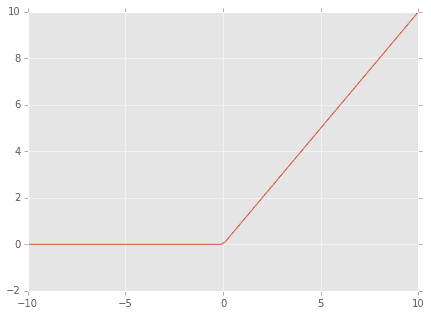
このF.relu()は正規化線形関数(Rectified Linear Unit function)で

f(x) = \max(0, x)

つまり

こんな感じです。
描画コードはこちら。

# F.reluテスト
x_data = np.linspace(-10, 10, 100, dtype=np.float32)
x = Variable(x_data)
y = F.relu(x)

plt.figure(figsize=(7,5))
plt.ylim(-2,10)
plt.plot(x.data, y.data)
plt.show()

シンプルな関数ですね。このため、計算量が小さく学習スピードが速くなることが利点のようです。

次に、このrelu()関数の出力を入力としてF.dropout()関数が使われています。

F.dropout(F.relu(model.l1(x)),  train=train)

このドロップアウト関数F.dropout()はDropout: A Simple Way to Prevent Neural Networks from Overfittingという論文で提唱されている手法で、ランダムに中間層をドロップ（ないものとする）し、そうすると過学習を防ぐことができるそうです。

ちょっと動かしてみましょう。

# dropout(x, ratio=0.5, train=True) テスト
# x: 入力値
# ratio: 0を出力する確率
# train: Falseの場合はxをそのまま返却する
# return: ratioの確率で0を、1−ratioの確率で,x*(1/(1-ratio))の値を返す

n = 50
v_sum = 0
for i in range(n):
    x_data = np.array([1,2,3,4,5,6], dtype=np.float32)
    x = Variable(x_data)
    dr = F.dropout(x, ratio=0.6,train=True)
    
    for j in range(6):
        sys.stdout.write( str(dr.data[j]) + ', ' )
    print("")
    v_sum += dr.data

# outputの平均がx_dataとだいたい一致する 
sys.stdout.write( str((v_sum/float(n))) )

output

2.5, 5.0, 7.5, 0.0, 0.0, 0.0, 
2.5, 5.0, 7.5, 10.0, 0.0, 15.0, 
0.0, 5.0, 7.5, 10.0, 12.5, 15.0, 
　　　　　　・・・
0.0, 0.0, 7.5, 10.0, 0.0, 0.0, 
2.5, 0.0, 7.5, 10.0, 0.0, 15.0, 
[ 0.94999999  2.29999995  3.          3.5999999   7.25        5.69999981]

[1,2,3,4,5,6]という配列をF.dropout()関数に渡します。いま、ratioはドロップアウト率であり、ratio=0.6を設定しているので、60%の確率でドロップアウトされ、0が出力されます。40%の確率で値が返されるのですが、その際、値を返す確率が40%に減ってしまっているので、それを補うために${1 \over 0.4}$倍=2.5倍された値が出力されます。つまり

(0 \times 0.6 + 2.5 \times 0.4) = 1

で、平均すると元の数字になるようになっています。上記の例だと最後の行が出力の平均ですが、50回繰り返して大体元の[1,2,3,4,5,6]に近い値になっています。

同じ構造がもう１層あり、出力され出力値が$y$となります。

    h2 = F.dropout(F.relu(model.l2(h1)), train=train)
    y  = model.l3(h2)

最後の出力ですが、ソフトマックス関数と交差エントロピー関数を用いて誤差の出力。それとF.accuracy()関数で精度を返しています。

    # 多クラス分類なので誤差関数としてソフトマックス関数の
    # 交差エントロピー関数を用いて、誤差を導出
    return F.softmax_cross_entropy(y, t), F.accuracy(y, t)

ソフトマックス関数ですが、

y_k = z_k = f_{k}({\bf u})={\exp(u_{k}) \over \sum_j^K \exp(u_{j})}

のように定義される関数で、この関数を挟むことで$y_1, \cdots ,y_{10}$の10個の出力の総和が1となり、出力を確率として解釈することが可能になります。
なぜ$\exp()$関数が使われているかというと、値がマイナスにならないように、ということと自分は理解しています。

おなじみ$\exp()$関数は

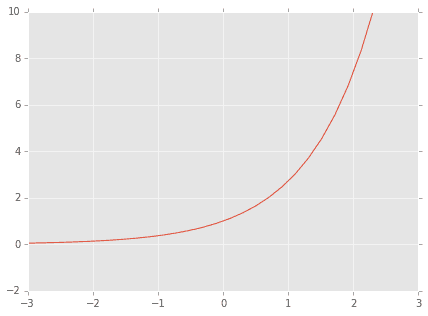
のような形なので、マイナスの値を取りません。これにより値がマイナスにならず、かつ総和が１ということになり、確率と解釈できるということですね。
さっきのソフトマックス関数の出力値$y_k$を用いて交差エントロピー関数は

E({\bf w}) = -\sum_{n=1}^{N} \sum_{k=1}^{K} t_{nk} \log y_k ({\bf x}_n, {\bf w})

と表現されます。

Chainerのコードで言うと、
https://github.com/pfnet/chainer/blob/master/chainer/functions/softmax_cross_entropy.py
にある、

def forward_cpu(self, inputs):
        x, t = inputs
        self.y, = Softmax().forward_cpu((x,))
        return -numpy.log(self.y[xrange(len(t)), t]).sum(keepdims=True) / t.size,

に相当します。

また、F.accuracy(y, t)は出力と、教師データを照合して正答率を返しています。

##3.3 Optimizerの設定##

さて、モデルが決まったので訓練に移ります。
ここでは最適化手法としてAdamが使われています。

# Setup optimizer
optimizer = optimizers.Adam()
optimizer.setup(model.collect_parameters())

Adamについては30分でわかるAdamでechizen_tmさんが解説してくれています。

#4.訓練の実施と結果#

以上の準備から、ミニバッチ学習で手書き数字の判別を実施し、その精度を見ていきます。

train_loss = []
train_acc  = []
test_loss = []
test_acc  = []

l1_W = []
l2_W = []
l3_W = []

# Learning loop
for epoch in xrange(1, n_epoch+1):
    print 'epoch', epoch

    # training
    # N個の順番をランダムに並び替える
    perm = np.random.permutation(N)
    sum_accuracy = 0
    sum_loss = 0
    # 0〜Nまでのデータをバッチサイズごとに使って学習
    for i in xrange(0, N, batchsize):
        x_batch = x_train[perm[i:i+batchsize]]
        y_batch = y_train[perm[i:i+batchsize]]

        # 勾配を初期化
        optimizer.zero_grads()
        # 順伝播させて誤差と精度を算出
        loss, acc = forward(x_batch, y_batch)
        # 誤差逆伝播で勾配を計算
        loss.backward()
        optimizer.update()

        train_loss.append(loss.data)
        train_acc.append(acc.data)
        sum_loss     += float(cuda.to_cpu(loss.data)) * batchsize
        sum_accuracy += float(cuda.to_cpu(acc.data)) * batchsize

    # 訓練データの誤差と、正解精度を表示
    print 'train mean loss={}, accuracy={}'.format(sum_loss / N, sum_accuracy / N)

    # evaluation
    # テストデータで誤差と、正解精度を算出し汎化性能を確認
    sum_accuracy = 0
    sum_loss     = 0
    for i in xrange(0, N_test, batchsize):
        x_batch = x_test[i:i+batchsize]
        y_batch = y_test[i:i+batchsize]

        # 順伝播させて誤差と精度を算出
        loss, acc = forward(x_batch, y_batch, train=False)

        test_loss.append(loss.data)
        test_acc.append(acc.data)
        sum_loss     += float(cuda.to_cpu(loss.data)) * batchsize
        sum_accuracy += float(cuda.to_cpu(acc.data)) * batchsize

    # テストデータでの誤差と、正解精度を表示
    print 'test  mean loss={}, accuracy={}'.format(sum_loss / N_test, sum_accuracy / N_test)

    # 学習したパラメーターを保存
    l1_W.append(model.l1.W)
    l2_W.append(model.l2.W)
    l3_W.append(model.l3.W)

# 精度と誤差をグラフ描画
plt.figure(figsize=(8,6))
plt.plot(range(len(train_acc)), train_acc)
plt.plot(range(len(test_acc)), test_acc)
plt.legend(["train_acc","test_acc"],loc=4)
plt.title("Accuracy of digit recognition.")
plt.plot()

epoch毎のサマリ結果はこちらです。20回しして98.5%くらいの高精度で判別できています。

output

epoch 1
train mean loss=0.278375425202, accuracy=0.914966667456
test  mean loss=0.11533634907, accuracy=0.964300005436
epoch 2
train mean loss=0.137060894324, accuracy=0.958216670454
test  mean loss=0.0765812527167, accuracy=0.976100009084
epoch 3
train mean loss=0.107826075749, accuracy=0.966816672881
test  mean loss=0.0749603212342, accuracy=0.97770000577
epoch 4
train mean loss=0.0939164237926, accuracy=0.970616674324
test  mean loss=0.0672153823725, accuracy=0.980000005364
epoch 5
train mean loss=0.0831089563683, accuracy=0.973950009048
test  mean loss=0.0705943618687, accuracy=0.980100004673
epoch 6
train mean loss=0.0752325405277, accuracy=0.976883343955
test  mean loss=0.0732760328815, accuracy=0.977900006771
epoch 7
train mean loss=0.0719517664274, accuracy=0.977383343875
test  mean loss=0.063611669606, accuracy=0.981900005937
epoch 8
train mean loss=0.0683009948514, accuracy=0.978566677173
test  mean loss=0.0604036964733, accuracy=0.981400005221
epoch 9
train mean loss=0.0621755663728, accuracy=0.980550010701
test  mean loss=0.0591542539285, accuracy=0.982400006652
epoch 10
train mean loss=0.0618313539471, accuracy=0.981183344225
test  mean loss=0.0693172766063, accuracy=0.982900006175
epoch 11
train mean loss=0.0583098273944, accuracy=0.982000010014
test  mean loss=0.0668152360269, accuracy=0.981600006819
epoch 12
train mean loss=0.054178619228, accuracy=0.983533344865
test  mean loss=0.0614466062452, accuracy=0.982900005579
epoch 13
train mean loss=0.0532431817259, accuracy=0.98390001148
test  mean loss=0.060112986485, accuracy=0.98400000751
epoch 14
train mean loss=0.0538122716064, accuracy=0.983266676267
test  mean loss=0.0624165921964, accuracy=0.983300005198
epoch 15
train mean loss=0.0501562882114, accuracy=0.983833344777
test  mean loss=0.0688113694015, accuracy=0.98310000658
epoch 16
train mean loss=0.0513108611095, accuracy=0.984533343514
test  mean loss=0.0724038232205, accuracy=0.982200007439
epoch 17
train mean loss=0.0471463404785, accuracy=0.985666677058
test  mean loss=0.0612579581685, accuracy=0.983600008488
epoch 18
train mean loss=0.0460166006556, accuracy=0.986050010125
test  mean loss=0.0654888718335, accuracy=0.984400007725
epoch 19
train mean loss=0.0458772557077, accuracy=0.986433342795
test  mean loss=0.0602016936944, accuracy=0.984400007129
epoch 20
train mean loss=0.046333729005, accuracy=0.986433343093
test  mean loss=0.0621869922416, accuracy=0.985100006461

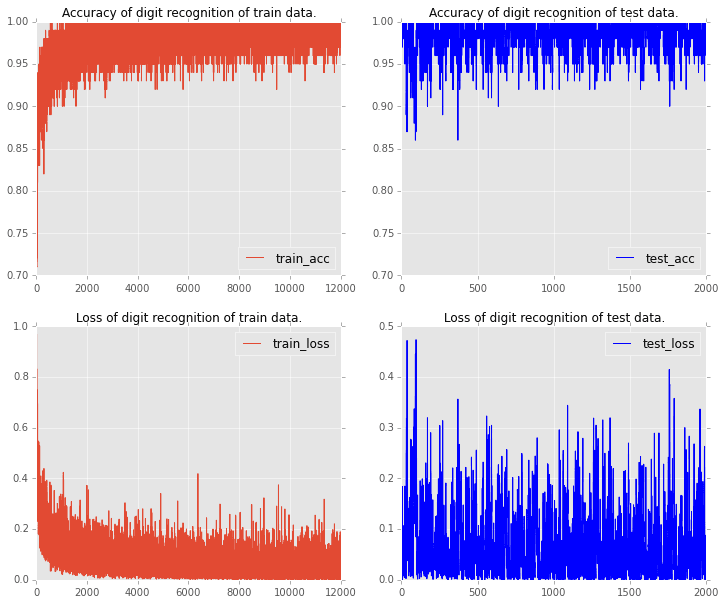
各バッチ毎の判別精度と、誤差のグラフがこちらです。赤いほうがトレーニングデータ、青いほうがテストデータになります。

以前、【機械学習】k-nearest neighbor method(k最近傍法)を自力でpythonで書いて、手書き数字の認識をするという記事で、同様に手書き数字の判別をやっていたのですが、その時の精度が97%くらいだったので、更に少し上がっていることがわかります。

このChinerは全てPythonコードで操作ができるので、非常にPythonistaとしては嬉しいフレームワークになっていると思います。まだ、「ディープ」ラーニングできておらず、ただのフィードフォワードニューラルネットワークなので、近々「ディープ」なやつの記事も書ければと思います。

#5.答え合わせ#

識別した100個の数字を表示してみます。ランダムに100個抽出したのですが、ほとんど正解です。何回か100個表示を行ってやっと間違っているところを１つ表示できたので、その例を下記に貼っています。なんだか人間の方が試されている気分です（笑）

（※ 2行3列の4を9と誤識別しています）

plt.style.use('fivethirtyeight')
def draw_digit3(data, n, ans, recog):
    size = 28
    plt.subplot(10, 10, n)
    Z = data.reshape(size,size)   # convert from vector to 28x28 matrix
    Z = Z[::-1,:]             # flip vertical
    plt.xlim(0,27)
    plt.ylim(0,27)
    plt.pcolor(Z)
    plt.title("ans=%d, recog=%d"%(ans,recog), size=8)
    plt.gray()
    plt.tick_params(labelbottom="off")
    plt.tick_params(labelleft="off")
    

plt.figure(figsize=(15,15))

cnt = 0
for idx in np.random.permutation(N)[:100]:
    
    xxx = x_train[idx].astype(np.float32)
    h1 = F.dropout(F.relu(model.l1(Variable(xxx.reshape(1,784)))),  train=False)
    h2 = F.dropout(F.relu(model.l2(h1)), train=False)
    y  = model.l3(h2)
    cnt+=1
    draw_digit3(x_train[idx], cnt, y_train[idx], np.argmax(y.data))
plt.show

#6.第１層のパラメータwの可視化#

入力層のパラメータ$w^{(1)}$784次元ベクトルを28x28ピクセルとしてマッピングして表示してみました。1000個のうちランダムに100個選んでいます。よくみると"2"とか"5"とか"0"に見えるものもありますね。1層目のパラメーターで特徴抽出ができていそうな雰囲気が伺えます。

def draw_digit2(data, n, i):
    size = 28
    plt.subplot(10, 10, n)
    Z = data.reshape(size,size)   # convert from vector to 28x28 matrix
    Z = Z[::-1,:]             # flip vertical
    plt.xlim(0,27)
    plt.ylim(0,27)
    plt.pcolor(Z)
    plt.title("%d"%i, size=9)
    plt.gray()
    plt.tick_params(labelbottom="off")
    plt.tick_params(labelleft="off")

plt.figure(figsize=(10,10))
cnt = 1
for i in np.random.permutation(1000)[:100]:
    draw_digit2(l1_W[len(l1_W)-1][i], cnt, i)
    cnt += 1
    
plt.show()

#7.出力層のパラメータwの可視化#

出力層は1000個のインプットを受けて、10個のアウトプットを行う層ですが、ここも可視化してみました。"0"と書いてあるところが手書き数字を"0"と判別するためのパラメーターです。

1000次元ベクトルなので、0を24個後ろにつけて32x32の画像に落としています。

# レイヤー3
def draw_digit2(data, n, i):
    size = 32
    plt.subplot(4, 4, n)
    data = np.r_[data,np.zeros(24)]
    Z = data.reshape(size,size)   # convert from vector to 28x28 matrix
    Z = Z[::-1,:]             # flip vertical
    plt.xlim(0,size-1)
    plt.ylim(0,size-1)
    plt.pcolor(Z)
    plt.title("%d"%i, size=9)
    plt.gray()
    plt.tick_params(labelbottom="off")
    plt.tick_params(labelleft="off")

plt.figure(figsize=(10,10))
cnt = 1
for i in range(10):
    draw_digit2(l3_W[len(l3_W)-1][i], cnt, i)
    cnt += 1
    
plt.show()

#8.おまけ#
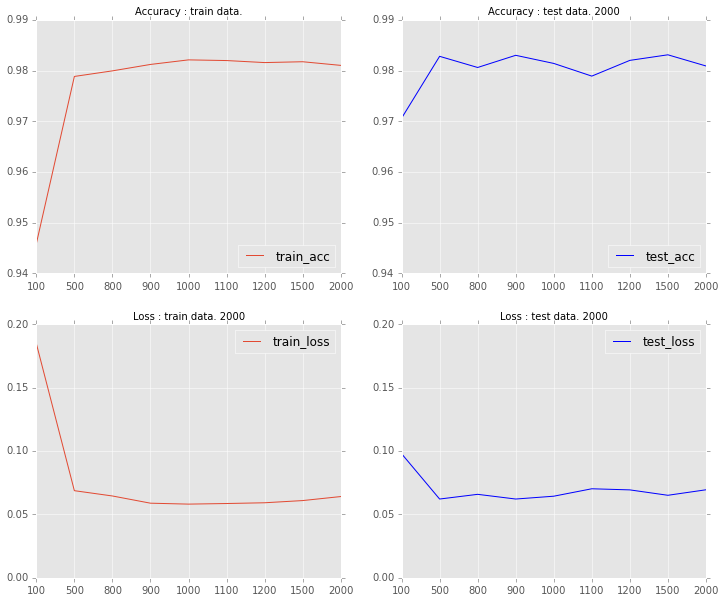
中間層の素子数を[100, 500, 800, 900, 1000, 1100, 1200, 1500, 2000]にしてそれぞれ判別してみた。結果のグラフが下記です。素子数500以上で概ね98%を達成しており、それ以上の素子数はあんまり変わらないみたいですね。

#9.おまけ2 : 活性化関数#

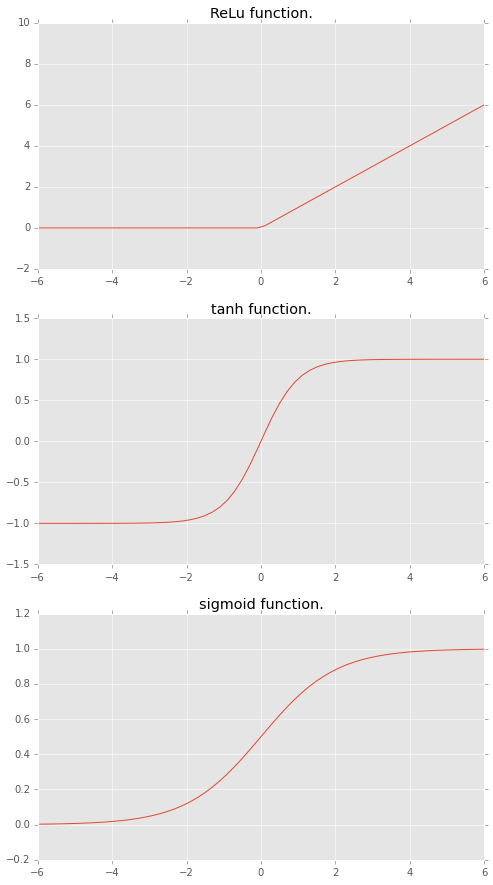
Chainerにプリインされている主な活性化関数に

• ReLu function
• tanh function
• sigmoid function

があります。図示すると下記のような形です。
素子の入力と出力の間に入る関数で、入出力に関する閾値を設定するような役割を持ちます。

# 活性化関数テスト
x_data = np.linspace(-10, 10, 100, dtype=np.float32)
x = Variable(x_data)

y = F.relu(x)
plt.figure(figsize=(8,15))
plt.subplot(311)
plt.title("ReLu function.")
plt.ylim(-2,10)
plt.xlim(-6,6)
plt.plot(x.data, y.data)

y = F.tanh(x)
plt.subplot(312)
plt.title("tanh function.")
plt.ylim(-1.5,1.5)
plt.xlim(-6,6)
plt.plot(x.data, y.data)

y = F.sigmoid(x)
plt.subplot(313)
plt.title("sigmoid function.")
plt.ylim(-.2,1.2)
plt.xlim(-6,6)
plt.plot(x.data, y.data)
plt.show()

次の記事
「【ディープラーニング】ChainerでAutoencoderを試して結果を可視化してみる。」
ディープラーニングで特徴抽出を自動化する技術のAutoencoderを実装してみた記事です。

【参考書籍】
　深層学習（機械学習プロフェッショナルシリーズ） 岡谷貴之
　

【参考webサイト】
　Chainerのメインサイト
　　　http://chainer.org/
　ChainerのGitHubリポジトリ
　　　https://github.com/pfnet/chainer
　Chainerのチュートリアルとリファレンス
　　　http://docs.chainer.org/en/latest/
　"Dropout: A Simple Way to Prevent Neural Networks from Overfitting"
　 Nitish Srivastava, Geoffrey Hinton, Alex Krizhevsky, Ilya Sutskever, Ruslan Salakhutdinov
　　　http://www.cs.toronto.edu/~rsalakhu/papers/srivastava14a.pdf