ChainerでAutoencoderを試してみる記事です。前回の記事、「【機械学習】ディープラーニング フレームワークChainerを試しながら解説してみる。」の続きとなります。ディープラーニングの事前学習にも使われる技術ですね。
本記事で使用したコードはコチラから取得できます。
#1.最初に#
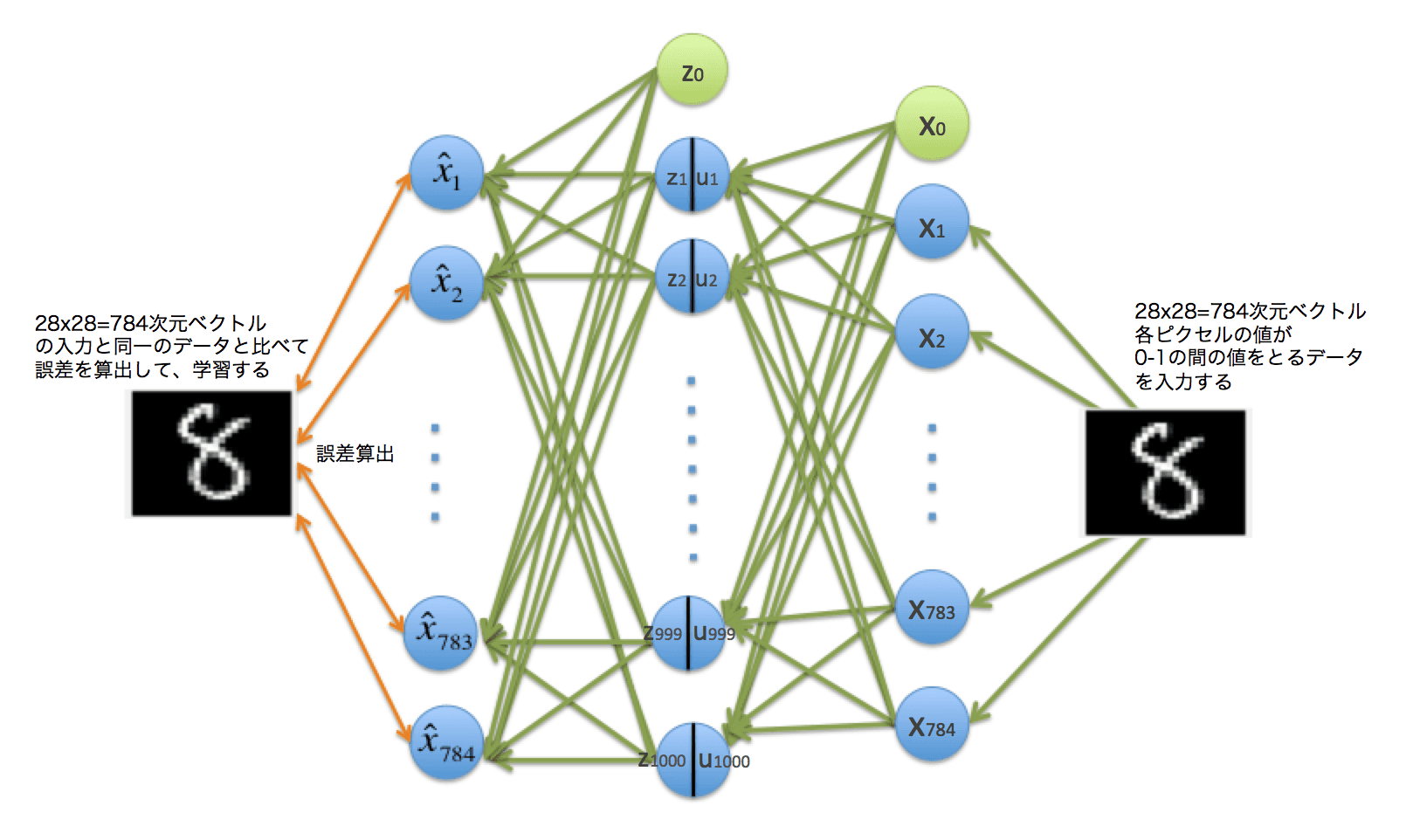
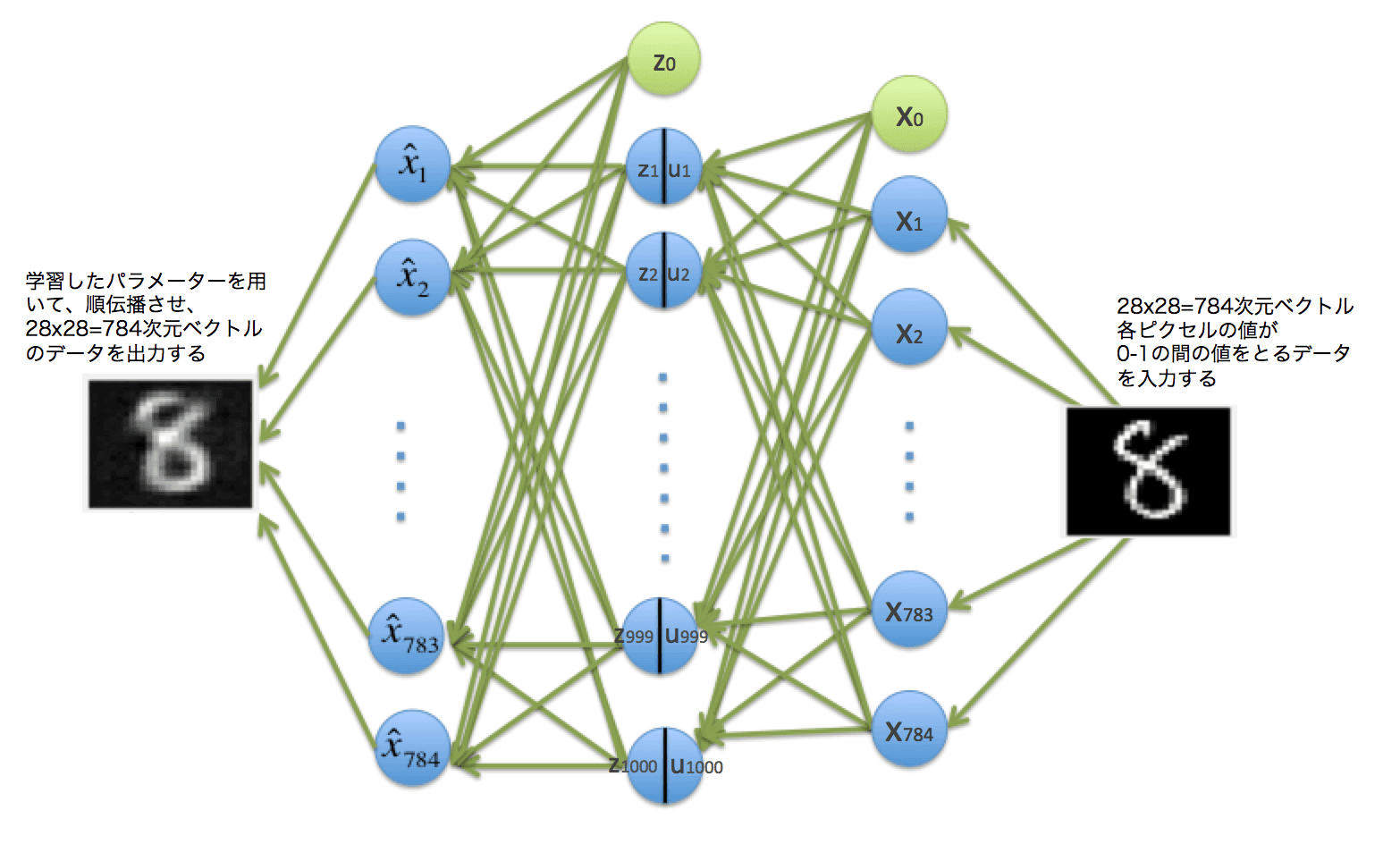
AutoencoderとはAuto(自己) encode(符号化)er(器)で、データを2層のニューラルネットに通して、自分自身のデータと一致する出力がされるようパラメーターを学習させるものです。データだけあれば良いので、分類的には教師なし学習になります。
学習フェーズ
こんなことをして何が嬉しいのかというと、
- 入力に合わせたパラメーター$w_{ji}$を設定できる。（入力データの特徴を抽出できる）
- その入力に合わせたパラメーターを使うことでディープなニューラルネットでの学習を可能にする（ランダム値より良い$w_{ji}$の初期値として利用）
ということができるのです。
出力実行
何はともあれ、動かしてみて可視化することを試みてみます。
#2.幾つかのパターンで動かしてみる#
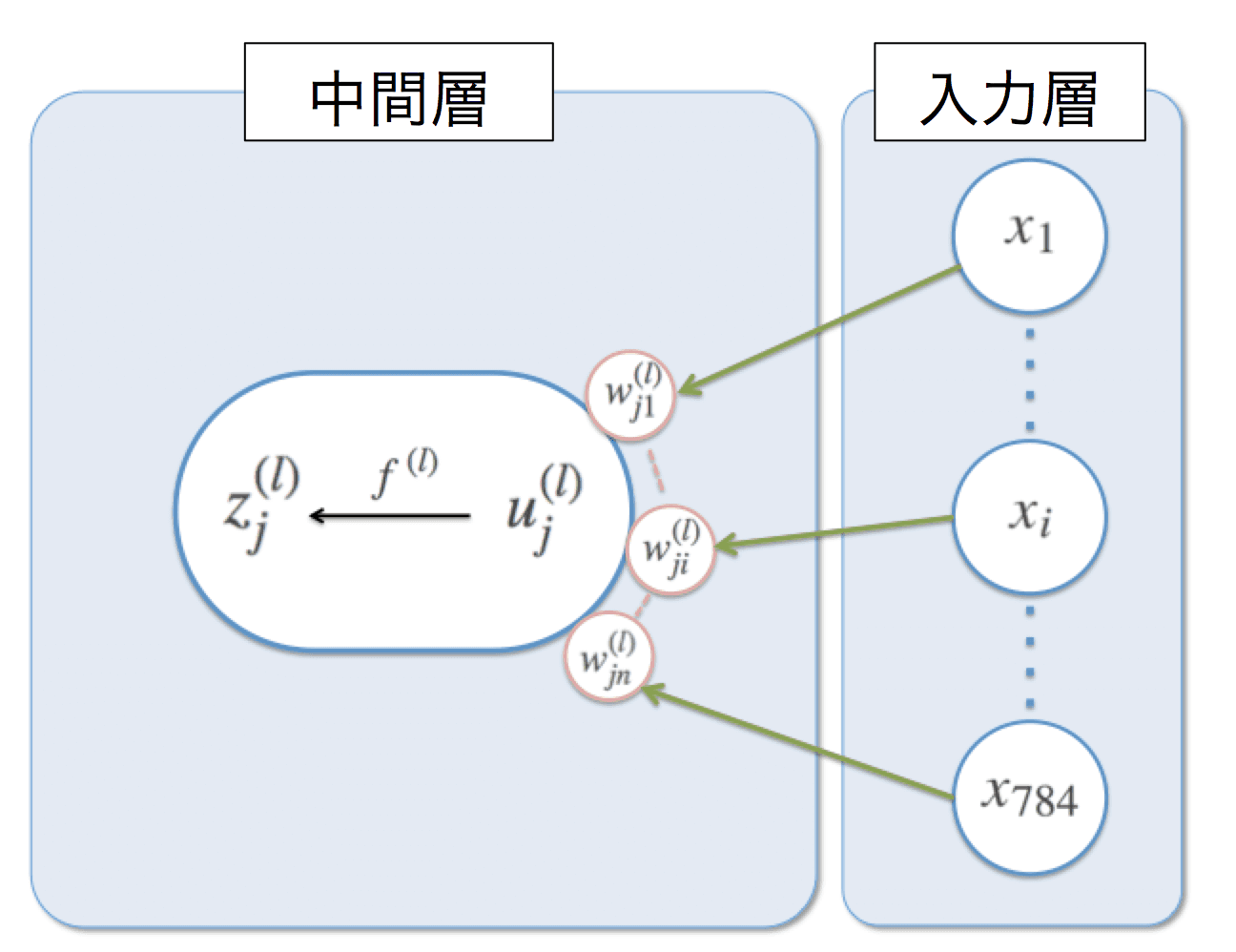
活性化関数に何を選ぶか、中間層の数はいくつにするか、Dropoutを行うか、ノイズを付加するか（Denoising Autoencoderとするか）、の組み合わせで７つのケースで試してみました。ちなみに活性化関数 $f(\cdot)$ は中間層の$u_j$と$z_j$の間に挟まっています。
こんな感じです。
実行したパターンの表
| 活性化関数 | 中間層数 | Dropout | ノイズ付加 | |
|---|---|---|---|---|
| ケース1 | ReLu | 1000 | あり | なし |
| ケース2 | ReLu | 1000 | なし | なし |
| ケース3 | ReLu | 400 | あり | なし |
| ケース4 | ReLu | 400 | なし | なし |
| ケース5 | Sigmoid | 1000 | あり | なし |
| ケース6 | Sigmoid | 1000 | あり | あり |
| ケース7 | Sigmoid | 100 | なし | あり |
ケース6, 7はいわゆるDenoising Autoencoderです。
今回もchinerのexample,
https://github.com/pfnet/chainer/tree/master/examples/mnist
┗ train_mnist.py
をベースに一部手を加えて作成しています。
#2-1.ケース1) ReLu, 1000ユニット, Dropoutあり#
ケース1のコード全文はこちらからご覧ください。
ポイントを抜き出して、その部分を中心に説明します。
モデルは2層、入力に28x28=784個のデータ。中間層ユニット数n_unitsは1000を設定しています。出力層も同様に28x28=784個のデータです。
# 中間層の数
n_units = 1000
# AutoEncoderのモデルの設定
# 入力 784次元、出力 784次元, 2層
model = FunctionSet(l1=F.Linear(784, n_units),
l2=F.Linear(n_units, 784))
活性化関数は中間層のみに適用しており、出力層は$f(\cdot)$は無し(つまり恒等関数)としています。誤差の算出には二乗誤差関数を使います。
# Neural net architecture
def forward(x_data, y_data, train=True):
x, t = Variable(x_data), Variable(y_data)
y = F.dropout(F.relu(model.l1(x)), train=train)
x_hat = F.dropout(model.l2(y), train=train)
# 誤差関数として二乗誤差関数を用いる
return F.mean_squared_error(x_hat, t)
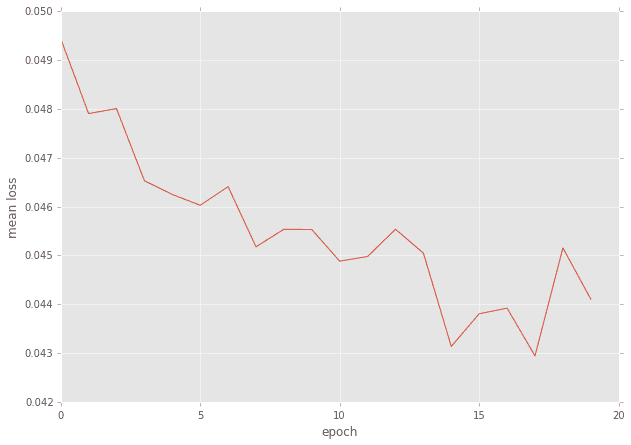
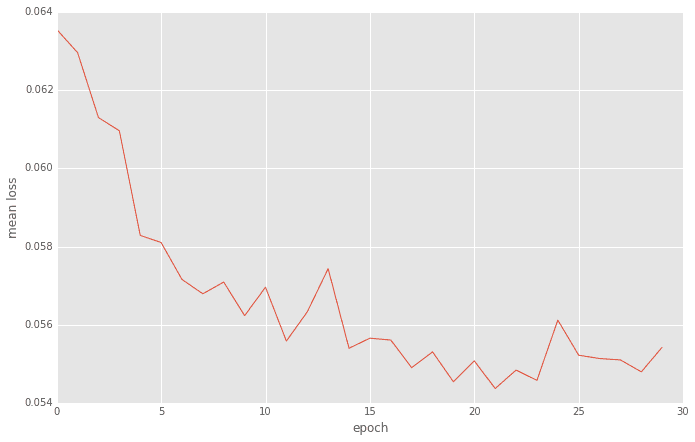
n_epoch=20として20回まわした時のバッチ毎の平均誤差の推移です。（もしかしたらもうちょっと回してもよかったかも？）
誤差の推移
入力データと出力データの比較がこちらです。上下２つずつの組で上が入力、下が出力になっています。ちょっとモヤがかかった感じですが、ほぼ再現されていることがわかります 
出力結果
面白いのがこのパラメーター$w_{ji}$の可視化です。7割くらいはノイズにしか見えないのですが3割くらいのパラメーターに手書き数字のストロークのようなものが浮き出ています。
1層目パラメーター$w^{(1)}_{ji}$の表示
出力層につながるところの$(w^{(2)}_{ji})$も可視化してみます。そのまま使うと1000次元ベクトルになってしまうのですが、転置して784次元ベクトル、つまり28x28の画像として解釈すると、こちらもまた特徴が浮き出ていることがわかります。こちらの層はストロークというよりは、数字のカタチそのままのものや、複数の数字が重ね合わさったカタチになっているように思えます。
2層目パラメーター$(w^{(2)}_{ji})^{\rm T}$の表示
#2-2.ケース2) ReLu, 1000ユニット, Dropoutなし#
ケース1のコードに1行修正を加えるだけです。
下記のように訓練処理時にforward()関数の引数trainをFalseとすると、Dropout関数がスルーされます。
loss = forward(x_batch, y_batch, train=False)
ちなみにこのケース2、一言で言うと**「過学習」**の臭いがします。
- 誤差がかなり小さくなった
- Autoencoderの出力の一致具合がハンパない
- パラメーター$w$がノイズにしか見えない
- そもそも、入力が784次元なのに、中間層のユニット数がそれを上回る1000次元
あたりが、そう思わせる根拠ですね。そう思うと、ケース1ではDropoutが上手く働いてきちんと過学習を防いでいた、と考えられるかと思います。
では、視覚的に見ていきましょう。
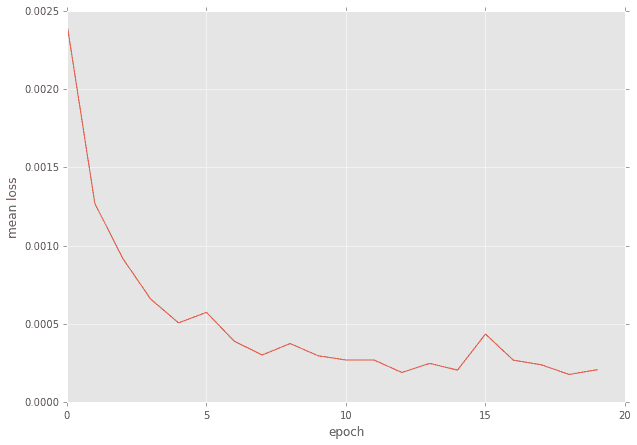
誤差の推移
ケース1では0.044付近でしたから、比べると誤差の桁が違うレベルで少ないです。
出力結果
ものすごい適合具合です 
適合というか、そのものですね。
1層目パラメーター$w^{(1)}_{ji}$の表示
あまり特徴的なものはみられず、稀に数字のカタチが見えるもの、なんらかドットのようなものを捉えているものがあるのみです。
2層目パラメーター$(w^{(2)}_{ji})^{\rm T}$の表示
こちらも1層目同様、うっすら数字のカタチのようなものも見えますが、非常にノイジーです。
#2-3.ケース3) ReLu, 400ユニット, Dropoutあり#
次に、中間層のユニット数を入力データ768より下げて400にしてみます。
これも、ケース1のコードに1行修正を加えるだけです。中間層ユニット数n_unitsを400にします。
# 中間層の数
n_units = 400
結果のサマリーとしては、全体的にケース1をモヤっとさせたもの、に仕上がっています。
誤差の推移
n_epoch=30で30回まわしてみましたが、20でも十分だったようです。
出力結果
霧がかかった感じですね、でも元の数字を再現できていると言えそうです。
1層目パラメーター$w^{(1)}_{ji}$の表示
ストロークもちょっと薄めの出方になりました。
2層目パラメーター$(w^{(2)}_{ji})^{\rm T}$の表示
１とか６とか８とかそのままのところもありますが、部分的な線のみ浮き出ているものもみられます。
#2-4.ケース4) ReLu, 400ユニット, Dropoutなし#
次は400ユニットに減らしたものでDropoutしないものです。下記の2点を変更します。
# 中間層の数
n_units = 400
loss = forward(x_batch, y_batch, train=False)
やはり過学習気味で、パラメーター$w$はほとんど人間には解読不能な出力となっています。
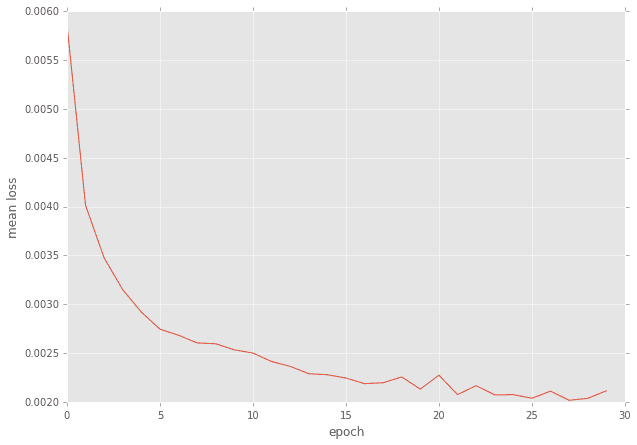
誤差の推移
overfittingのせいか、このケースも誤差は非常に少ないです。
出力結果
1層目パラメーター$w^{(1)}_{ji}$の表示
謎の模様です。入力データの特徴を反映して縁の方は平坦になっているものが多いようです。
逆にノイズのような出力は無くなりますね。
2層目パラメーター$(w^{(2)}_{ji})^{\rm T}$の表示
２層目も謎の模様です。
#2-5.ケース5) Sigmoid関数, 1000ユニット, Dropoutあり#
次に活性化関数をSigmoid関数に変えてみます。F.relu()を使っていたところをF.sigmoid()に差し替えるだけです。2箇所あります。
y = F.dropout(F.sigmoid(model.l1(x)), train=train)
h1 = F.dropout(F.sigmoid(model.l1(Variable(xxx.reshape(1,784)))), train=False)
誤差の推移
誤差はReLuの時とほぼ同程度のようです。
出力結果
若干薄めですがかなりよい復元具合かと思います。
1層目パラメーター$w^{(1)}_{ji}$の表示
パラメーター$w$の特徴はReLu関数よりも捕らえられているように思います。というのも、全くのノイズしかない成分というのがかなり少ないためです。
2層目パラメーター$(w^{(2)}_{ji})^{\rm T}$の表示
2層目についても視覚的に意味のありそうなパターンが多く出ており有用に感じます。
#2-6.ケース6) Sigmoid関数, 1000ユニット, Dropoutあり, ノイズ付加#
入力データに10%のノイズを乗せてそれをノイズを乗せる前のデータと近くなるように学習します。ここではノイズとして0で上書きするように指定します。いわゆるDenoising Autoencoderです。
ノイズ付加フラグをTrueにします。
# ノイズ付加有無
noised = True
すると、学習用データに20%の割合でノイズ（0でピクセルを上書き）が加えられます。
# 学習用データを N個、検証用データを残りの個数と設定
N = 60000
y_train, y_test = np.split(mnist.data.copy(), [N])
N_test = y_test.shape[0]
if noised:
# Add noise
noise_ratio = 0.2
for data in mnist.data:
perm = np.random.permutation(mnist.data.shape[1])[:int(mnist.data.shape[1]*noise_ratio)]
data[perm] = 0.0
x_train, x_test = np.split(mnist.data, [N])
ノイズが乗ったデータを見てみるとこんな感じです。
# Visualize noised image
p = np.random.permutation(len(mnist.data))[:10] # sampling 10pcs of images
plt.figure(figsize=(12,4))
for i in range(len(p)):
draw_digit_ae(mnist.data[p[i]], i+1, 2, 5, "noised")
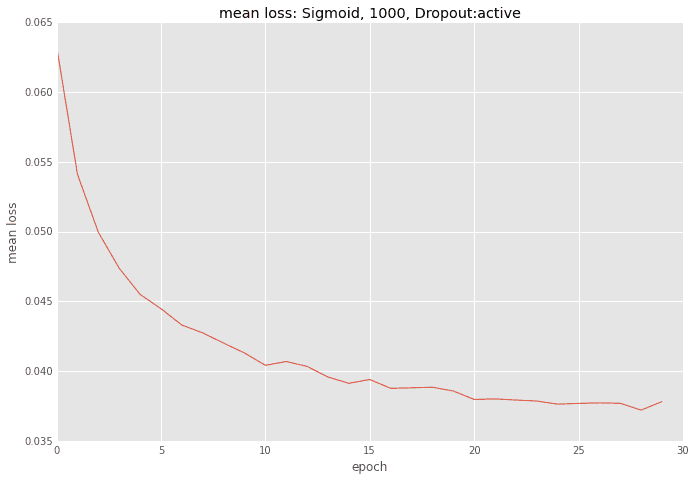
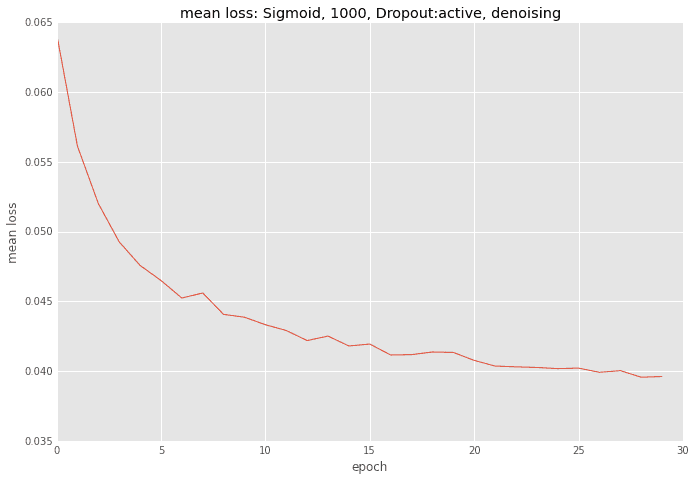
誤差の推移
出力結果
入力データをノイズが乗っていないものに変更します。
xxx = y_test[idx].astype(np.float32)
ans_list.append(y_test[idx])
1層目パラメーター$w^{(1)}_{ji}$の表示
2層目パラメーター$(w^{(2)}_{ji})^{\rm T}$の表示
#2-7.ケース7) Sigmoid関数, 100ユニット, Dropoutなし, ノイズ付加#
このケースが一番効率が良さそうに思います。再現性も高く、それがユニット数100で可能となっています。ただし、$w$について第2層目に特徴が現れてしまっているので、それを第1層に出せるような方法を探す事がよう検討事項です。
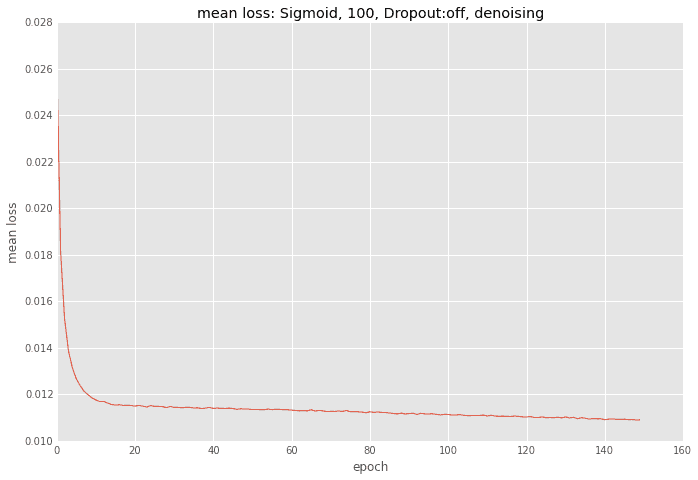
誤差の推移
回数は多いですが、ユニット数が少ないのでひと回しに時間がかからないため、トータルでもさほど時間はかかりません。
847d-f20a-c0a4e12a2d24.png)
出力結果
綺麗に再現できています。
1層目パラメーター$w^{(1)}_{ji}$の表示
若干特徴薄めで、ドットらしきものがうっすら見える程度です。この層に特徴を入れたいので課題です。
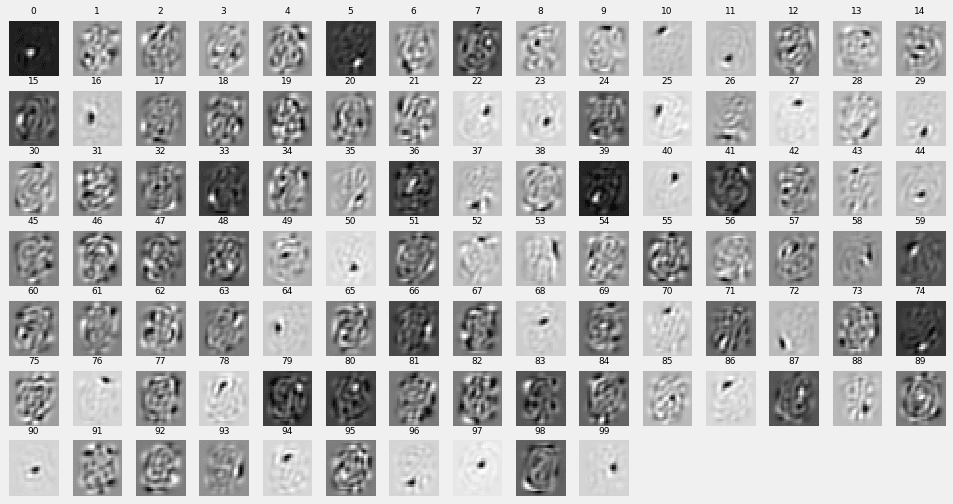
2層目パラメーター$(w^{(2)}_{ji})^{\rm T}$の表示
この層に特徴がよく表れています。ストロークではなく、ドットのようなもので特徴があらわされています。
【参考】
先日、「深層学習」本の勉強会で畳込みニューラルネットについて説明してきましたので、
よろしければそのスライドもご覧ください。
【参考書籍】
深層学習（機械学習プロフェッショナルシリーズ） 岡谷貴之
【参考webサイト】
Chainerのメインサイト
http://chainer.org/
ChainerのGitHubリポジトリ
https://github.com/pfnet/chainer
Chainerのチュートリアルとリファレンス
http://docs.chainer.org/en/latest/