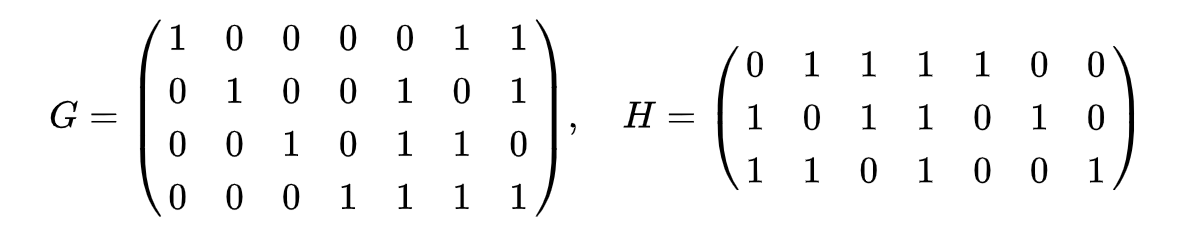概要
Berlekamp-Massey algorithm からスタートして、符号理論を全く知らないことに気づき、まわりまわって線形符号、アダマール符号などについて勉強してみたので備忘録的にまとめました。
内容
どれも日本語と英語のウィキペディアをベースに勉強しただけになります。
ハミング距離
ハミング距離とは、2つのベクトルが与えられた時、各要素を比べて行って、異なる要素があるたびにカウントを増やし最後のカウントの出力のことです。
たとえば、$10010$と$11011$のハミング距離は、2つの要素が異なるので2になります。
言い換えると、2つのベクトルが与えられた際に、片方のベクトルの幾つの要素を変更すれば他方と等しくなるかをカウントしたものです。
そもそも、符号とは
符号とは、誤り訂正に使われる手法です。情報を送信者から受信者にノイズのある条件下で送る、つまり受信者は受け取った情報にノイズがあるかもしれず、あったならノイズを検出し訂正する必要がある。という状況化で、受信者にその手段を与えます。
ブロック符号における最小距離
ブロック符号は、$(n, k, d)_q$ のような表記をされることが多く、それはブロック符号に使われるブロックのサイズがnであり、メッセージの長さ(送るブロックの個数)はk個であり、その符号の最小距離がdである。というような意味です。
ここで、最小距離とは、いかなるペアの異なるメッセージが符号化された時の、最小のハミング距離のことで、次のようにかかれます。
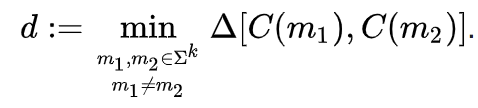
この最小距離がdのとき、$d/2 -1 $以下のエラー個数であれば、受信側で訂正ができます。
線形符号
線形符号は誤り検出訂正に使われるブロック符号のうちの1種類になります。他の符号に比べて、符号化と復号化が効率的であるという特徴を持ちます。
とりあえず、有限体の拡大体を考えた際、それがn次元線型空間であるとします。その中のk次元線型空間を(n,k)線形符号と呼びます。k次元線型空間Cはk個の基底ベクトル($g_1, g_2, .., g_k \in F^n $)を指定することで定まるが、それらの基底ベクトルを並べた$n \times k$の行列を線形符号$C$の生成行列($G$)と呼びます。また、Cを連立一次方程式で指定することも往々に可能であり、その時に用いる行列のことをパリティ検査行列($H$)と呼びます。線形符号$C$の基底を上手くとることで、下図のような形式に$G$および$H$を取ることができます。このような$G$、$H$を組織符号形式と呼びます。

よって、例えば入力ベクトルが$k$次元だった場合、まず生成行列によって$n$次元の符号を作り送ります。受信者はパリティ検査行列と受信した情報を用いてシンドロームを生成。シンドローム表から対応するコセット・リーダを計算し、それを受信した情報から引き算することでエラーを訂正できます。
のような場合、この符号は $[7,4,3]$ と書くことができ、1ビットのエラーを訂正することができます。
このハミング符号と呼ばれる方式に関しては、訂正能力に関して、$[2^r-1, 2^r -r -1, 3]_2$ の符号です。
アダマール符号
アダマール符号に関しては、$[2^r, r, 2^{r-1}]_2$の符号であり、符号化により多くのデータを送らなければならない反面、多くのビット($r^{r-2}-1$個)を訂正可能である。
アダマール符号はアダマール行列からきており、アダマール行列とは各行が直行しているという条件を持つ行列のことで、
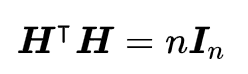
それは上記の条件に書き直せる。また、アダマール行列の生成は再帰的に行うことができ、
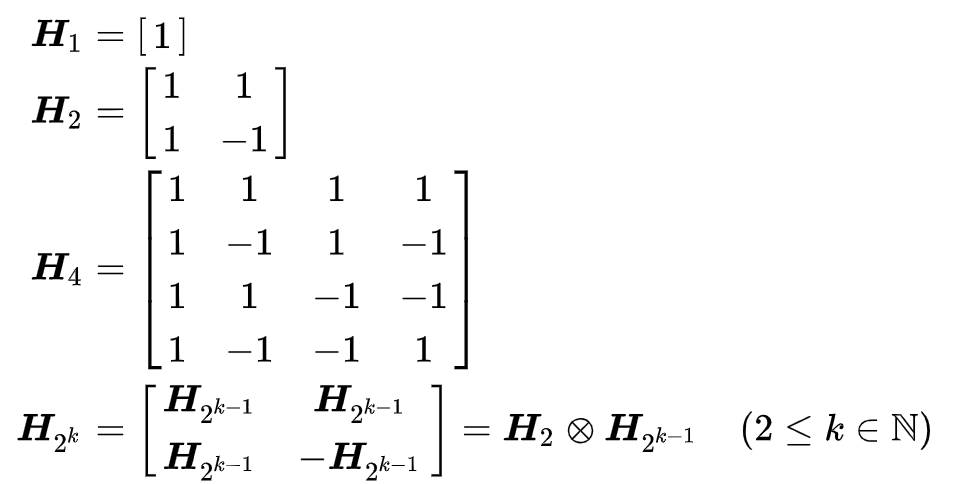
それはこう書けます。
終わりに
今回はここまで。
終わり。