概要
以前に書いた、ニューラルネットの積分表現やリッジレット変換を勉強するにあたって、ルベーグ積分という言葉が出てきた。学生時代にきちんと勉強しなかったなあという思いから、少しだけ調べてみて、フビニの定理までできたら行きつきたいと思ったときの、備忘録になります。
フビニの定理とは
ウィキペディアより、
数学においてフビニの定理（フビニのていり、英: Fubini's theorem）とは、Guido Fubini (1907) によって導入された、逐次積分による二重積分の計算が可能となるための条件に関する一結果である。すなわち、次のような計算が可能となる。
$\int_X\left(\int_Y f(x,y)\,\text{d}y\right)\,\text{d}x=\int_Y\left(\int_X f(x,y)\,\text{d}x\right)\,\text{d}y=\int_{X\times Y} f(x,y)\,\text{d}(x,y).$
この結果、積分の順序（英語版）は逐次積分において変えることが可能となります。
おそらく押さえておきたい言葉たち
- 測度
- 可測
- 可測集合
- リーマン和（リーマン可積分性）
- ダルブー (Darboux) の定理
- 完全加法族
- ルベーグ測度
- 可測集合
- ルベーグ外測度
- （1 次元）ルベーグ測度 (Lebesgue measure)
まあ体力的にとりあえずこの辺で。
参考にした講義資料など
などです。あくまでも備忘録としてのまとめなので、興味のある方はこれらの参考文献に飛ぶとハッピーだと思います。
内容
ルベーグ積分は、高校で習うリーマン積分の拡張になります。積分を、対象となる関数$f$と、集合$X$を与えられたときに実数を返すような写像と見ると、
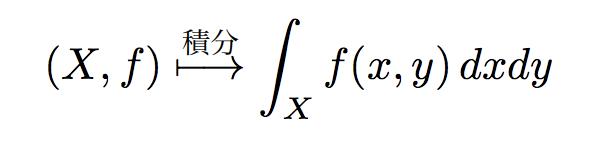
となります。
リーマン積分
リーマン和とは、ある定義域を分割し、関数の代表点を分割された定義域に含まれる代表点で評価し、足し合わせることです。
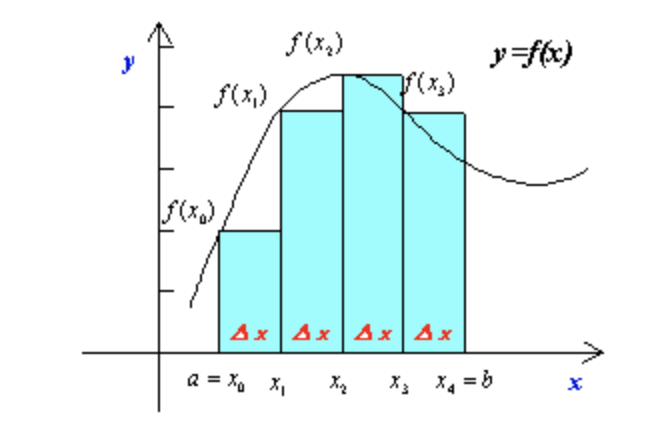
また、ダルブーの定理とは、リーマン和において、分割の幅を小さくとることで、代表点をどうとるかに関係なく、リーマン積分の値がある値に収束していくことを示す時に使う定理です。
ルベーグ積分
ルベーグ積分は定義域を分割するのではなく、値域を分割します。
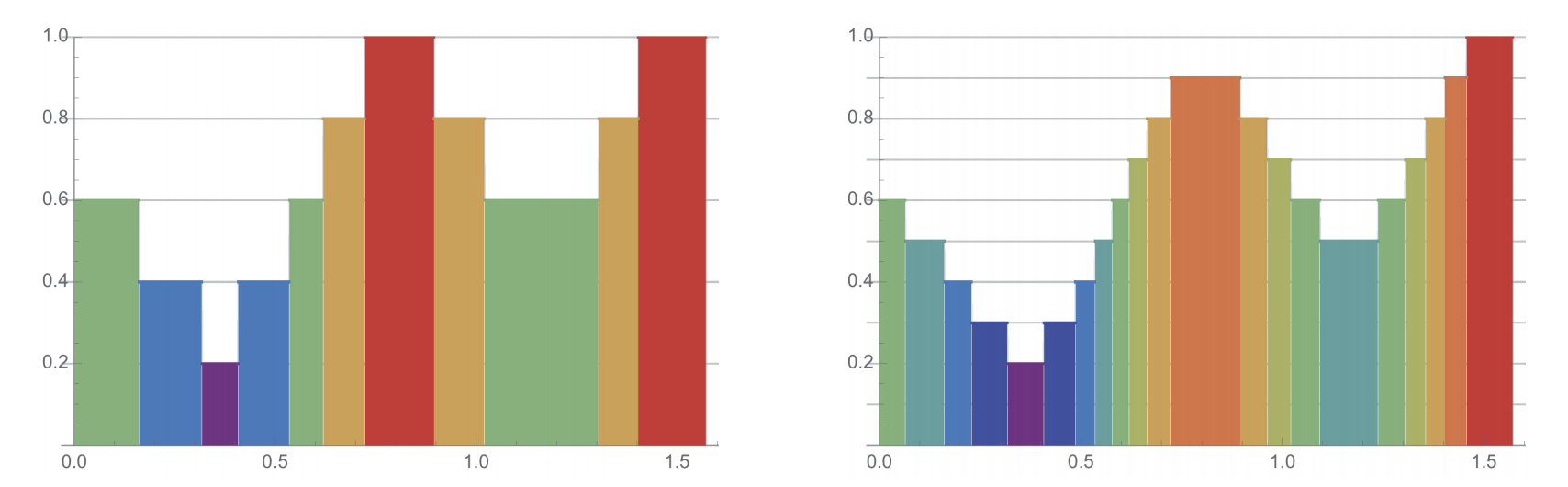
すなわち、同じ値を持つもの同士がグループとなり、そのグループに何個要素があるかを数え上げ、それに関数値をかけることで積分を評価するわけです。
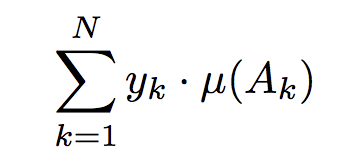
そのとき、例えば上のように、$y_k$は関数値、$\mu(A_k)$が$y_k$に対応するグループを足し上げたもの、と書くことができるとします。このとき、どうやって$\mu(A_k)$を得ることができるか、ということをルベーグ積分の中で考えていくわけです。
完全加法性
このとき、集合族とは、Sの要素がXのある部分集合であるという意味。言い換えると、SはXの部分集合を集めた集合であり、EはSの要素である、すなわちXのある部分集合になります。
ルベーグ測度
測度、ここではルベーグ測度を考える時、上の与えられた$A_k$という集合の長さを測るような写像$\mu$が必要です。具体的には上の完全加法性を持った族、完全加法族$E$を用いて、
wikipediaより。
の要請を満たすような$\mu$であり、これをルベーグ測度と呼びます。
ルベーグ外測度
$I = [a, b) := {x ∈ R \ \ | \ \ a ≤ x < b} $を考えた時、ルベーグ外測度は、以下のように定義されます。まず、Rの部分集合からなる列集合を用いて、被覆という言葉の定義を行うことで、ルベーグ外測度を定義できます。ルベーグ外測度はRの任意の部分集合を、定義された$I$の和集合の下界に、飛ばすときの写像の事です。
可測集合
という問題に関しては、成り立たない場合があるため、可測集合を以下のように定義する。
ルベーグ測度
上で定義された可測集合に制限したルベーグ写像（ルベーグ外測度）を、以下のように定義し、ルベーグ測度と呼ぶ。
とりあえず
一度ここで終わりにして、フビニの定理にたどり着けるように頑張ります。
おわり。