注意)この記事は専門用語などを極力排除し、簡単な例を提示しています。イメージだけ掴んでもらう記事ですのでご了承ください。
この記事の目的
TFHEで行われるブートストラップ手法を、できるだけビジュアライズする。
準同型暗号 とは
格子暗号について少し調べたことのある人であれば、この章はすんなりと理解できると思います。
格子暗号とは、準同型暗号とよばれる暗号の内の一つであり、
準同型暗号は「暗号に対しても足算や掛け算のような演算を
実行できる」つまり「暗号状態のまま計算できる」という点でユニーク、注目の集まる暗号分野です。
TFHE とは
TFHE は0、1のビットを暗号化し、任意のビット回路を暗号状態で実行できる格子暗号の形式の一つです。
また、ライブラリも提供されており、その実装はおそらく現時点で最速のビット回路演算を実行できるものです。
原論文 https://duckduckgo.com/?q=TFHE+homomorphic&t=raspberrypi&ia=web
ライブラリ https://github.com/tfhe/tfhe
ブートストラップ とは
格子暗号の暗号文には、「ノイズ」と呼ばれるものがセキュリティを保証するために加えられています。
問題となるのは、暗号文に対して計算(特に掛け算)を行っていくにつれ、このノイズが増大していくことです。
このノイズが増大しすぎると、復号が不可能になります。
「ブートストラップ」とは、この暗号文に付随しているノイズを「暗号状態のまま」小さくするテクニックです。
ブートストラッピングを行うことによってノイズをリセット可能なので、
実質「任意の長さの」ビット回路演算を実行可能になります。
つまり、暗号に対してどんな演算でも可能で、途中で復号などは必要ありません。
TFHEで実装されているのはこのブートストラップを用いて暗号文同士のNAND回路などを計算する、
ゲートブートストラッピング と呼ばれるものです。
論文を読もうとするととても難しい。。
しかしながら、実際にブートストラップを解説している文献や論文を読むととても難解に感じることも多いと思います。
今回は、数式や専門用語をほとんど使わずにTFHEのブートストラップについてまとめていけたらと考えています。
解説
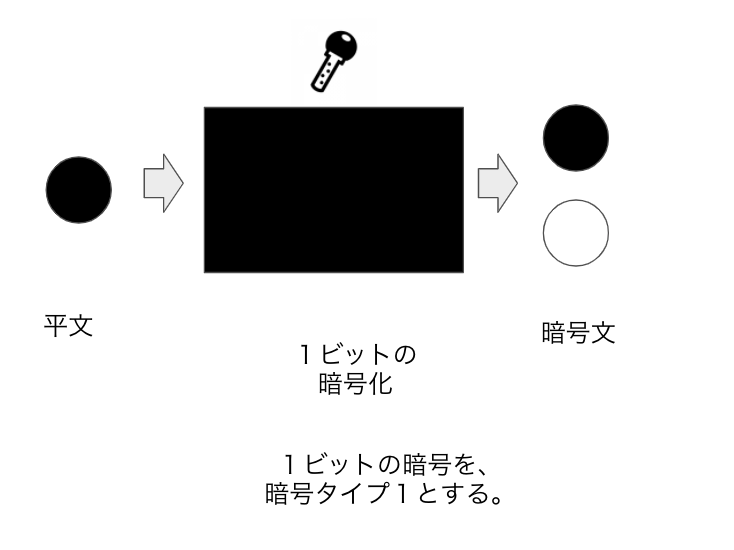
とりあえずビットの0を黒色のオセロで、1を白色のオセロで表すことにします。
暗号化により、入力のオセロは出力のオセロに変換されます。
この出力のオセロの色から入力の色を類推が難しいことは、
暗号が基づいているセキュリティ問題(LWE問題と呼ばれます。)によって担保されることになります。
タイプ1とタイプ2の暗号文
ここで、1ビットを暗号化したときの暗号文を暗号タイプ1と呼ぶことにします。
(このタイプ1と呼ぶ暗号文は、TLWEサンプルのことです。)
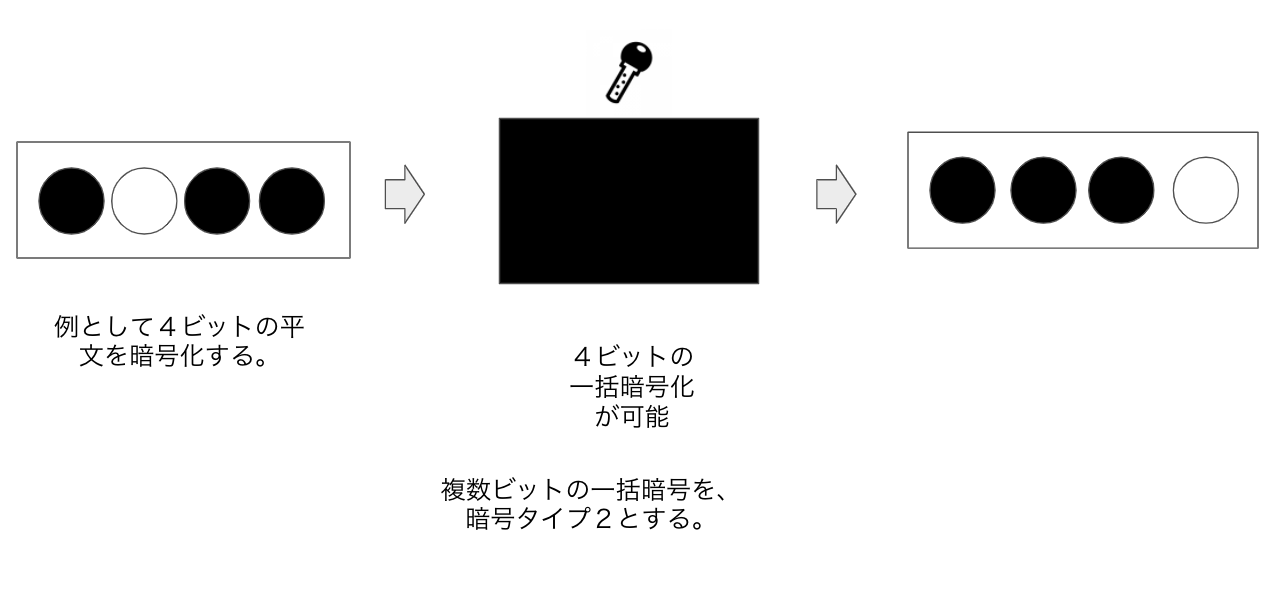
格子暗号では、複数のビット(ここでは例として4ビット)を一括で暗号化することができます。
こうして作られた暗号を暗号タイプ2と呼ぶことにします。
(このタイプ1と呼ぶ暗号文は、TRLWEサンプルのことです。)
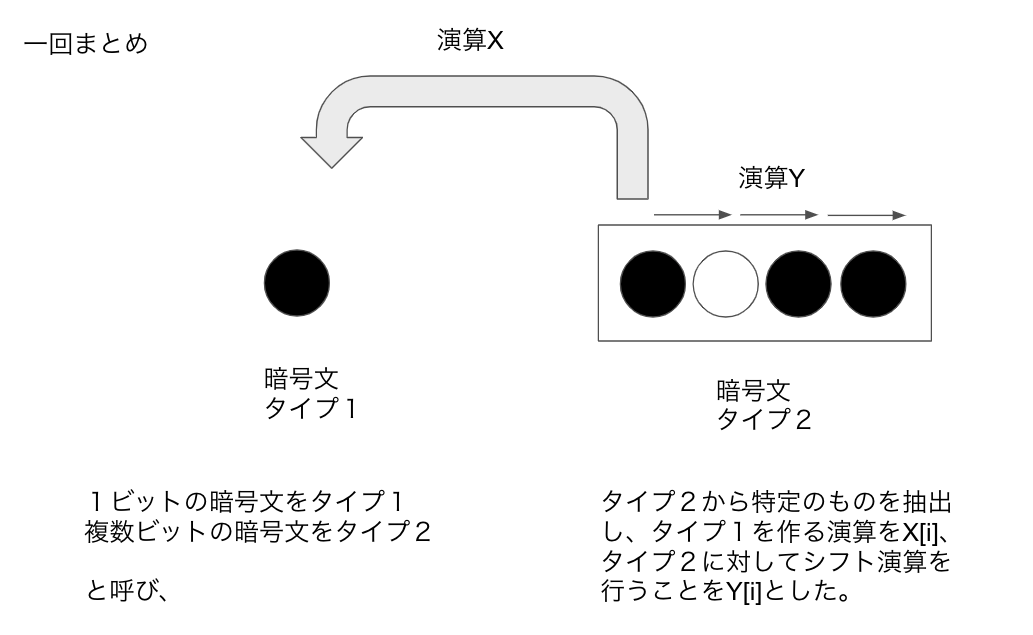
抽出演算X
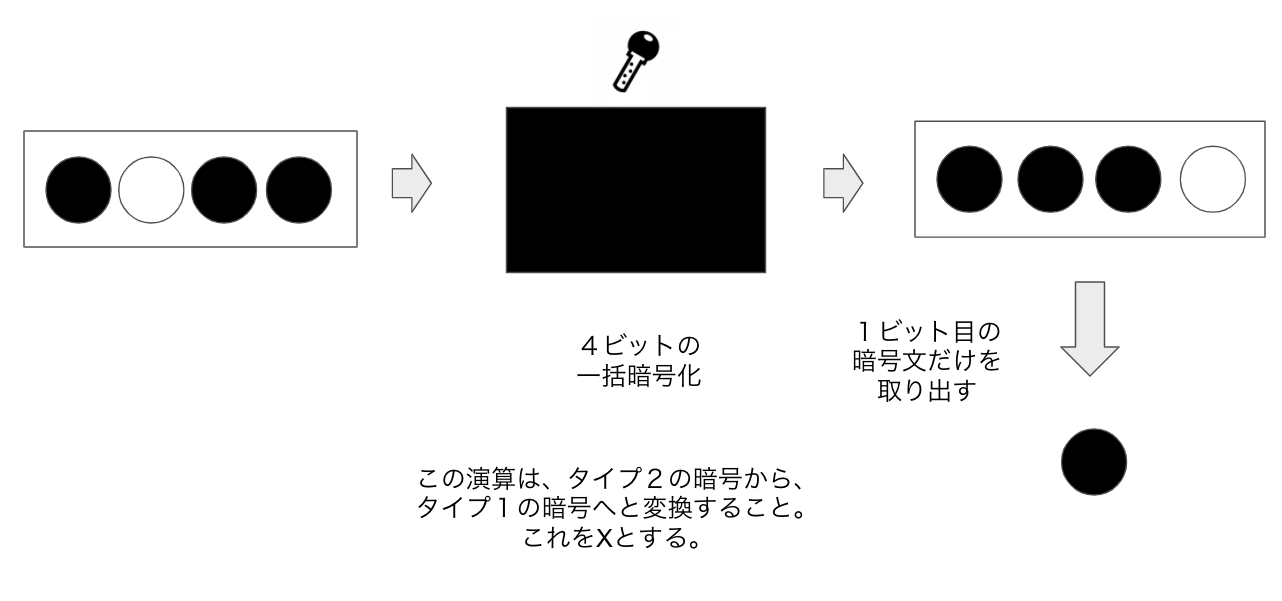
タイプ1とタイプ2には関連があり、タイプ2からタイプ1を作ることが可能です。
タイプ1は1ビットの暗号化なので、複数ビットを暗号化しているタイプ2から「抽出」を行うイメージで大丈夫です。
(この抽出演算Xは、SampleExtractionのことです。)
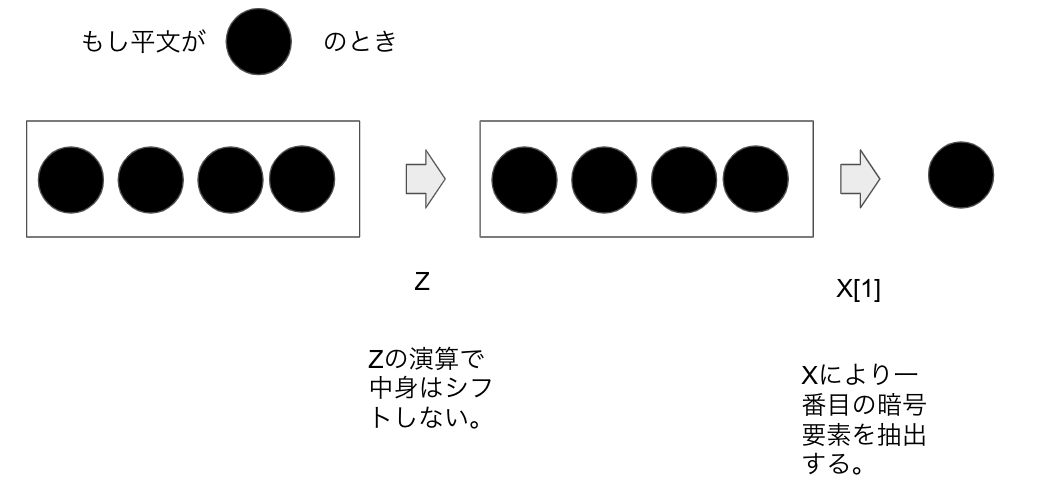
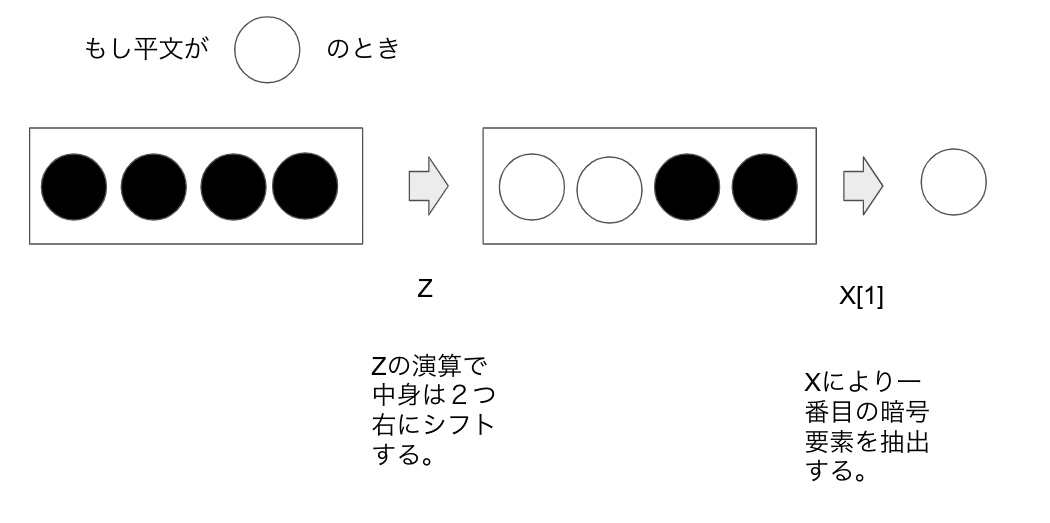
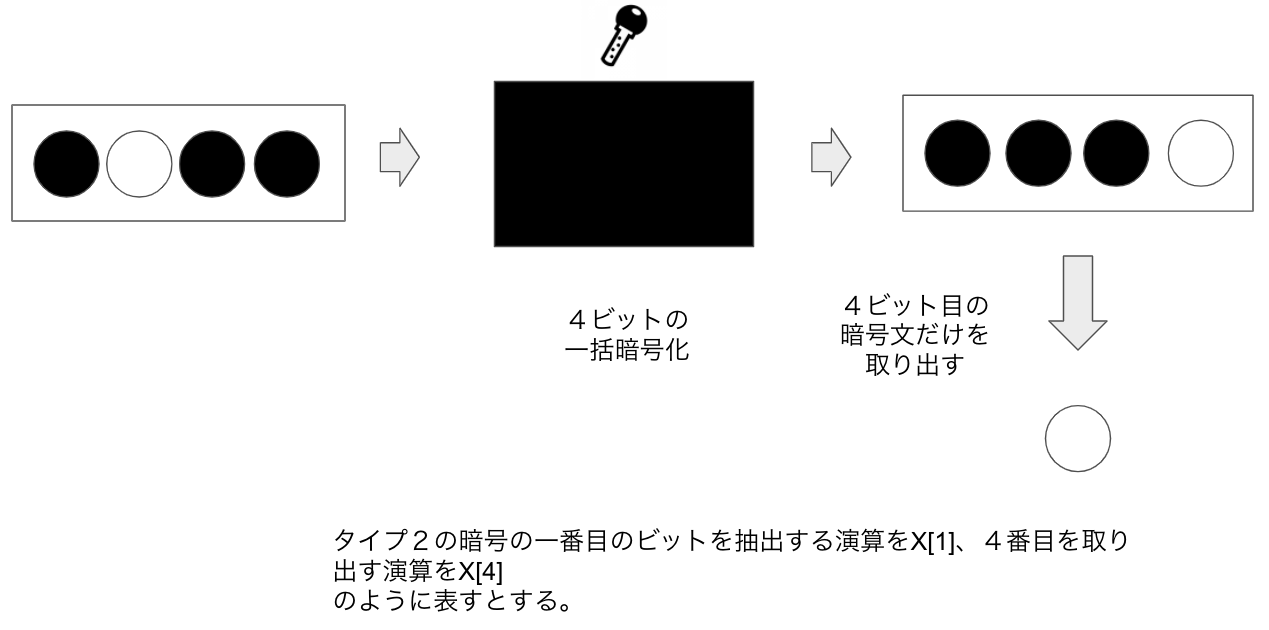
例として、一番目のビットの暗号文をタイプ1の形で取り出す演算をX[1] と定義、
4番目のビットの暗号文をタイプ1の形で取り出す演算をX[4]と定義します。
シフト演算Y
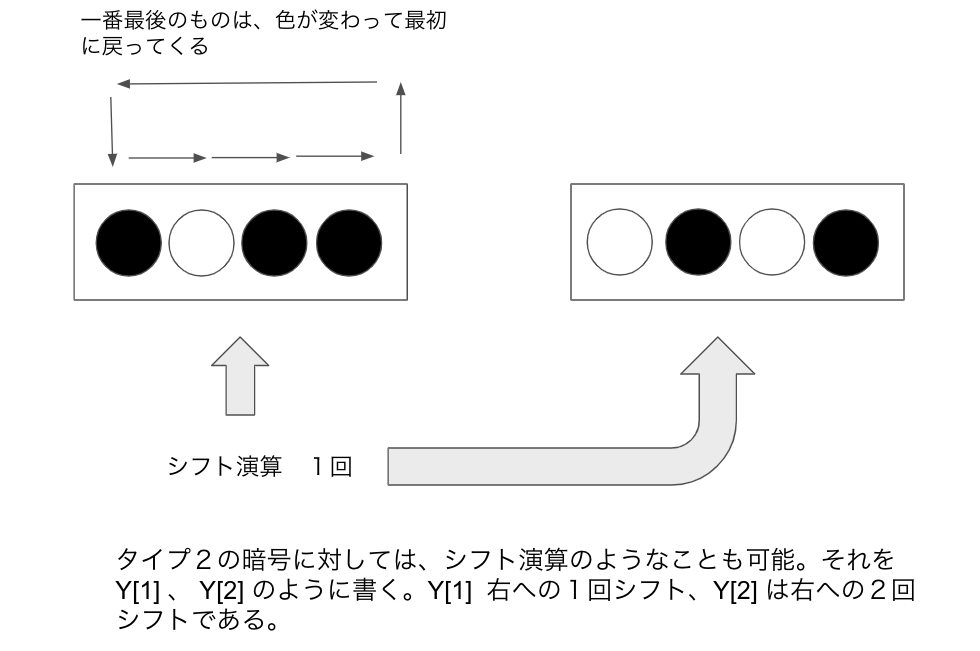
タイプ2に対して、シフト演算を行うことができます。
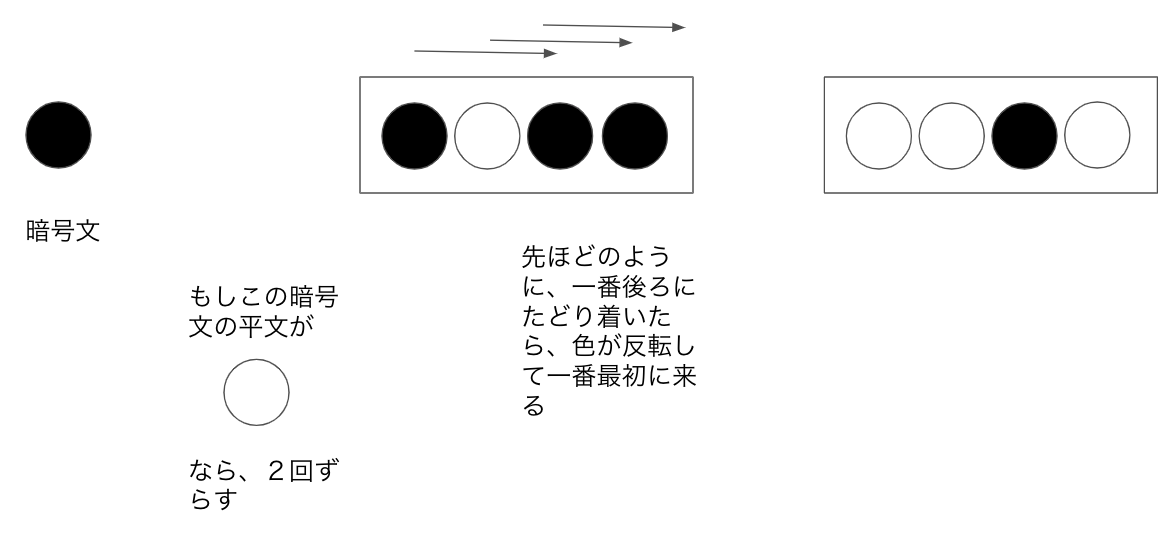
要素を右にシフトする時に、**最後の要素は色が反転して最初の要素に戻ってきます。**
1回シフトをY[1] 、2回シフトをY[2]と書くことにします。
(このシフト演算Yは、GaloisMappingのことです。)
一旦まとめ
演算Z
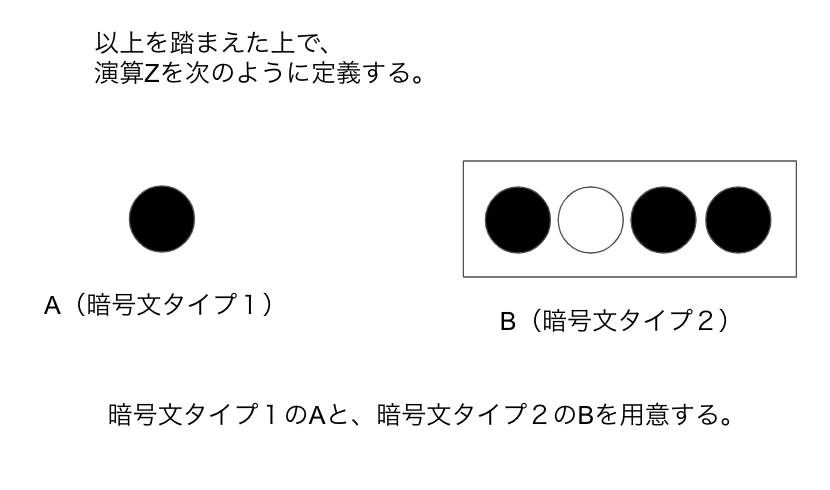
演算Zを定義するために、 タイプ1の暗号文Aと、タイプ2の暗号文Bを用意します。
暗号文Aの平文が白色だったか、黒色だったかはもちろん秘密鍵なしには分かりません。
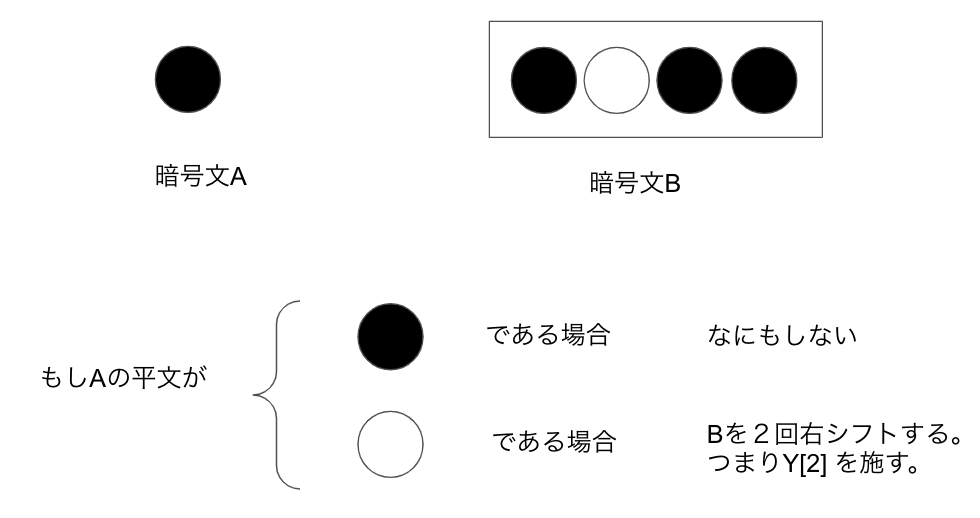
しかしながら、もし黒であればなにもせず、白であれば先ほどのシフト演算Yを行うような 演算を定義することが可能です。
(すこしややこしいですが、暗号文Aを復号する時の関数から吐き出される情報(Phaseと呼ばれます。)分だけ、暗号文Bをシフトする演算になります。)
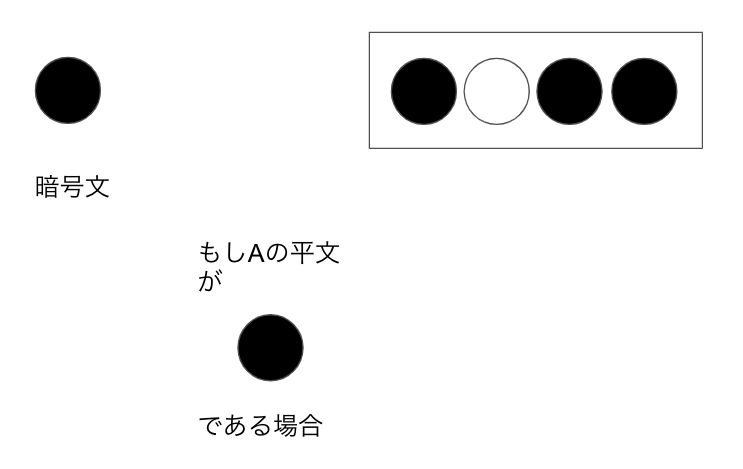
例として、もしAの平文が黒色だったときは、何もしません。
つまり暗号Bがそのまま演算Zから出力されます。
もしAの平文が白色だったときは、Bが2回右シフトされたものがZの演算結果として出力されます。
ここで、では演算Zの出力を見れば、
暗号Aの平文が白であったか、黒であったかと思った人もいるかと思います。
確かにこの説明では、Zの出力をみると暗号Aが何を暗号化しているかわかってしまいます。
しかしながら、これはこのオセロの例を用いているからです、
どうしてもここをうまく説明するにはオセロの例では難しかったです、すみません。
きちんとお伝えしないといけないことは、実際の演算Z(論文では BlindRotate と呼ばれます。)
では、Zの出力からAの平文の情報が漏れるようなことはありません。(原論文のCMuxを使用します。)
演算Zに関して掴んで欲しいのは、 暗号Aを「復号すること」もしくは「平文の情報を漏らすこと」なしに、 暗号Bに暗号Aの「平文の情報に応じて」シフト演算を実行できる、 ということです。
ブートストラッピング手順
ここまでで、
- タイプ1の暗号
- タイプ2の暗号
- 演算X
- 演算Y
- 演算Z
が出てきました。
これらを使うことで、ブートストラップの手順が説明可能になります。
ここで最後にX[1] によって抽出された暗号タイプ1の暗号文(Cとします)
は、新しく生成されたBという暗号文から抽出されたものなので、ノイズの大きさが一定です。
つまり、ブートストラップを施した時の出力Cには、一定の大きさのノイズが含まれるだけであり、それはAの持っていたノイズより
遥かに小さいものになっています。
さらに、Cは平文としてAが暗号化していたものと同じものを持っているため、
CはAのコピーのようなものであり、ノイズだけが低減されたタイプ1の暗号文であることになります。
したがって、続くブーリアン回路では、ノイズのたまったAの代わりにCを使用することができます。
しばらくしてCにまたノイズがたまった場合、またCにブートストラップを実行し、新しいタイプ1の暗号文をCのコピーとして使用する。
これを繰り返すことで、ノイズを爆発させることなく、任意の長さの回路を暗号状態のまま実行することができる、
これが全体の流れです。
おさらい
タイプ1の暗号文Aがあり、復号を行うことなくそれのノイズを小さくする、
という目的のもと
ブートストラッピングの手順を以下のように定義しました。
-
タイプ2の暗号文Bを作る。作るときは、全ての要素が0(黒色)を暗号化するように作っておく。 -
A、Bを入力とし、演算Zを行う。これにより、BはAの平文に関連した情報分だけ、シフト演算を施されて出力される。出力はタイプ2の暗号文である。 - 上の出力に対し
X[1]を実行する。出力はタイプ1の暗号文である。 - 上の出力は暗号化している平文として、Aと同じものを持っておりノイズだけが小さくなっている。したがって目的が達成された。
今回は、数式を使わずにブートストラップがなにをやっているか、
なるべく簡単にまとめたつもりです。
演算Zのところは少し疑問が残るような書き方になってしまいましたが、
もし興味のある方は上のTFHEの原論文の CMux, BlindRotate について一読してみると厳密なアルゴリズムをみることができます。
まとめ
もちろんいろいろな論文をがっつり読み込んで、アルゴリズムを理解できればいいのですが、
なかなか数学の前提知識や、参考文献に翻弄されたりしてなかなか理解しにくいブートストラップ手法。
もしこの記事を読んでイメージだけでも掴んでいただけたら幸いです。
オセロの例に関しては、なるべく簡単にしたかったのでいい加減なことも書かれているかと思いますがご容赦ください。
興味のある方は、TFHEの原論文が60ページと長いですが、かなり丁寧に1から解説してある教科書のような論文となっておりますのでご覧ください。
今回はこの辺で。
kenmaro