概要
秘密計算は、データを秘匿したまま演算や分析を実行するための技術の総称のことですが、
いろいろな手法を駆使して、目的は
ユーザのデータを秘匿したまま活用し、データの分析に役立てる
ということだと思います。
今回は、2022年にAlibabaの研究グループから発表された
こちらの論文について解説したいと思います。
秘密計算を利用し、画像分析のバックボーンとしてよく使われる
ResNet50を80秒程度で推論できる、
という論文です。
正直なところ準同型暗号を用いているレイヤは理解できたのですが、
秘密分散を用いて実行している非線形演算の高速化のところは知識があまり足りず、完全には追えませんでした。
今後この記事はまたアップデートしたいと思っています。
忙しい人のためのまとめ
- この論文の実装(Cheetah)では、ResNet50を準同型暗号、2パーティの秘密分散で秘匿推論しているよ
- 準同型暗号を用いた線形演算部分でも新しい高速化を用いて提案しているよ
- 秘密分散を用いた非線形演算部分でも新しい高速化手法を用いて提案しているよ
- WAN環境(インターネット通信環境)でも、ResNet50は150秒くらいで推論できるよ
- この結果は先行研究(CrypTFlow2) より10倍以上速いよ
それでは、みていきます。
先行研究たち
2パーティ間で通信を行いながら秘密分散手法を利用し、
かつ準同型暗号も用いて通信量と演算時間を抑える工夫を取り入れた(ハイブリッド手法)
ニューラルネットの推論の先行研究は、
- DELPHI
- CrypTFLow2
などがありました。
なぜハイブリッドなのか?
なぜ準同型暗号と秘密分散(加法秘密分散法を使用)を組み合わせて演算を工夫しているのでしょうか。
理由は、
- 準同型暗号(格子暗号)がもっているSIMD演算により、格子暗号を用いれば線形演算が比較的高速に実行可能なこと
- 加算秘密分散法により、非線形演算が必要な時に格子暗号から秘密分散法にスイッチし、非線形演算が実行困難な格子暗号の欠点を補えること
の2つのメリットがあるからです。
先行研究の問題点
しかしながら、SIMD演算を実行する構成で格子暗号を組もうとすると、
選択する加算秘密分散法で扱うPrime Field は、Z_p に限られていました。
Z_{2^l} (環を使う手法)も選択肢として考えられる加算秘密分散法において、
環を使うとより高速で通信を抑えた状態で非線形演算を行えるため、
SIMD演算を利用するメリットを残しながら、Z_{2^l} を加算秘密分散法として扱うような構成が今までされてこなかったこと、
が今までの問題だったと語られています。
本研究の工夫
- 上記の様にZ_{2^l} を利用した構成を構築したこと
- 線形演算のエンコードを工夫し、暗号の回転操作を全く行わないような構成にしたこと
- 加算秘密分散法上での比較演算、及びオーバーフローを防ぐためのトランケーションアルゴリズムを高速化したこと
と書かれています。
線形演算部分の高速化
ResNetはRes ブロックと呼ばれる残差接続を行うレイヤーが
何回も繰り返されます。
Resブロックの主な構成要素は
- 畳み込み層(Conv2D)
- バッチノーマライゼーション
で構成されますが、
今回は両方のレイヤを準同型暗号のSIMD演算を用いることで、
さらに、回転操作を行わずに演算を完結させるために
https://qiita.com/kenmaro/items/1b6fc7a053bb55111e64
以前ここで紹介した、係数パッキングを用い、基本的にはCRTパッキングを用いない方針で演算を構築しています。
さらに、バックボーンの後に必要な全結合層についても、
同様に係数パッキングを用いてCRTパッキングを使わずに構成しています。
係数パッキングを用いれば、多項式同士の掛け算で計算される畳み込みの性質がうまく使えることを
上記した以前の記事でお伝えしましたが、まさにそれを最大限上手く活用しています。
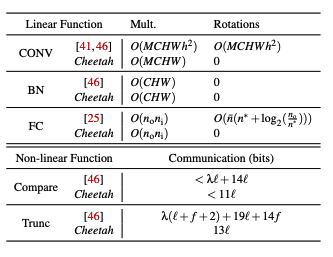
論文内2章のテーブル1を参照すると、
畳み込み層、バッチノーマライゼーション、全結合層においてRotationがいずれも0回となっていることがわかります。
非線形演算部分の高速化
さて、非線形演算部分ですが、
主に二つの構成要素があることがわかります。
論文内4.1に言及されている比較演算についてと、
4.2で言及されている掛け算を行った後のトランケーションです。
比較演算
比較演算は、
- ReLU 関数の評価
- プーリング関数の評価
で大量に使われます。
4.1で言及されている高速化
lビットの整数を入力とするときの比較演算ですが、
比べたい2つの入力をx, y とします。
4.1に書かれているプロトコルのステップ1において、
lビットの整数をmビットの塊にまずわけ、
そのmビットに対して2^m to 1 の紛失通信を使うことで、
そのmビットの塊x、yのどちらが大きいかを計算します。
ステップ2では、
それらの結果を合わせて最終的なlビットの入力同士の比較演算としています。
4.2 で言及されているトランケーションプロトコルの高速化
4.2.1では、トランケーションを行う際の2つのエラーに対して、
一方のエラーは1ビット分のエラーであり、DNNアプリケーションについてはその影響が低いことにより
それについてはビット訂正をあえて行わないことで高速化しています。
4.2.2では、ReLUを通した後のトランケーションについて、MSBはReLU関数を通った後は自明にゼロとなることから、
1ビットをわかっている状態でのトランケーションを高速化しています。
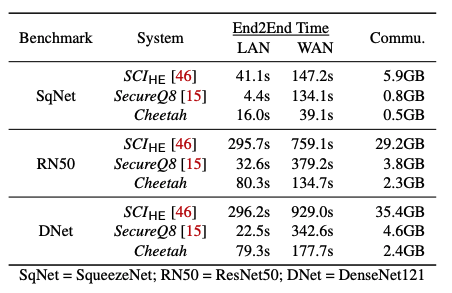
実装結果
上記の様に、バックボーンとして使われた
- SqueezeNet
- ResNet50
- DenseNet121
で上記の様な秘匿演算ができています。
また、精度は12ビットの整数を使っています。
これは
- 準同型暗号のみを用いた構成
より圧倒的に速度が早く、
- 秘密分散だけを用いた構成
より圧倒的に通信データ量が抑えられています。
私が今まで読んだ論文の中でも、
一番実用性に近い実装であることは間違いなさそうです。
まとめ
今回は、Alibabaのリサーチグループが発表した
2パーティ構成の秘密計算でResNet50を推論する実装
について解説したつもりでしたが、少し途中で力尽きてしまい、
また、秘密分散の分野の知識が足りないため、もう少し理解するには時間が必要だと考え、
軽く内容をさらっただけの解説になってしまいました。
秘密計算にはいろいろな要素があり、
それらを上手く組み合わせることでより実用的で、なおかつセキュリティにも配慮した構成のアプリケーションが作れるということは以前の記事でもお話ししたつもりですが、この実装は
- 準同型暗号
- 秘密分散
を両者共に現在の応用技術的には最高レベルのものを使ったときの、
秘密計算の今の実力かなあと思いました。
応用論文については、この内容がもしある程度理解できて、
実装も可能になればかなり凄いのではと思います。
他にもたくさんの実装、研究開発の結果が論文として出てきていますので、
自分ももう少しついていける様にしたいと思いました。
みなさんも興味があればぜひもっと深掘り、他の論文にもチャレンジしてみてください。
今回はこの辺で。