More than 3 years have passed since last update.

暗号解説シリーズ　情報理論の父シャノンでも解けなかった　究極の暗号「バーナム暗号」を解説！！

暗号理論

Posted at 2020-02-02

バーナム暗号

バーナム暗号は、1917年にアメリカのギルバート・バーナムが考え出した暗号である。
方や、アメリカの数学者であったクロード・エルウッド・シャノンは情報理論の父と呼ばれ、暗号理論への業績が華々しい。
バーナム暗号は、そのシャノンでも解読できなかった（実際は、絶対に解読できないことを証明したのだが）暗号であり、究極の暗号と呼ばれている。

####この記事の流れ

シャノンについての簡単な説明
ワンタイムパッド
- シーザー暗号
- バーナム暗号
問題点
- 完全ランダム生成
- セキュアな乱数共有
- 乱数の使い回し防止
量子鍵配送
- BB84プロトコル
- 研究が進む量子鍵配送
まとめ

0. 少しだけシャノンについて

情報系の学生であれば、クロード・エルウッド・シャノンの名前を一度は聞いたことがあると思います。彼はアメリカの数学者で、情報理論の父と呼ばれていますが、その功績はすごすぎるものです。

誤り訂正符号という現在のデータ伝送での最も重要な概念を導入した。
標本化定理を証明した。
エントロピーの概念を導入した。
情報量の単位としてビットを初めて使用した。

このシャノンが、完全安全証明をした、バーナム暗号とはどんな暗号なのでしょうか。
このバーナム暗号は、その完全安全性により、ワンタイムパッドとよばれる手法で用いられます。

1. ワンタイムパッド

ワンタイムパッドとは、一度きりで使える暗号手法のことで、生成された乱数とそれによって暗号文を別々に送り、受信者が乱数を用いて安全に伝達された暗号文を解読できる手法のことである。
シャノンによってこのワンタイムパッドは以下の条件で完全安全証明がなされている。つまり、一定の条件下で絶対に破られることのできない、究極の暗号である。条件は以下の通り。

乱数が完全ランダムであること
乱数は少なくとも平文と同じ長さであること。
乱数は一度の使い切りで、二度と使いまわされることがないこと。
乱数は完全に秘匿されなければならないこと。

上記に従い、暗号送信者は通信量と同じ長さの完全乱数を使用し、平文を暗号化、送信する。一度情報が伝達されると、日めくりのように1回使った乱数表は捨てる。
ただし、３，４のとおり運用方法の誤りで解読可能となる場合がある。乱数表の流出はもちろんだが、乱数の使いまわしも暗号強度の低下を招くので注意が必要である。

この絶対に破られることがないという究極の性質上、第二次世界大戦などで米軍や日本軍などで使われていた。乱数を紙に書いておいて、一度使うと捨ててしまうことから、トイレットペーパー暗号とも呼ばれていたらしい。繰り返しになるが一度使った乱数を使いまわすことはできないが、それについてのエピソードとして、乱数を使いまわしてしまったことで戦時中のスパイ活動が摘発されてしまったというストーリーがある。戦場で回収された暗号表が米国NSAに回され、OTP乱数表を前線と米国駐在情報官の両方で使った事に気がついたことから、乱数表が解析されてしまったらしい。

1.1 具体例

バーナム暗号をわかりやすく図式化する前に、シーザー暗号を理解しておくと非常に都合が良い。このシーザー暗号は歴史がとても古く、紀元前１世紀の共和制ローマ時代、ジュリアス・シーザーが考案したことから「シーザー暗号」と呼ばれているが、それは単純ながらどんなメッセージでも暗号化できるとても汎用的なものとなっている。

1.1.1 シーザー暗号

シーザー暗号は単純なアルゴリズムに基づいた古典暗号のひとつである。カサエル式暗号、シフト暗号とも呼ばれる(カサエルは英語読みでシーザーになります)。シーザー暗号は、鍵となる「何個アルファベットをシフトするか」という整数を決め、それを暗号鍵とします。例えば、それぞれの文字を「３つ」づつずらすというルールの場合、平文の「a」→ 暗号文の「d」、「b」→「e」、「c」→「f」という具合に暗号化される。

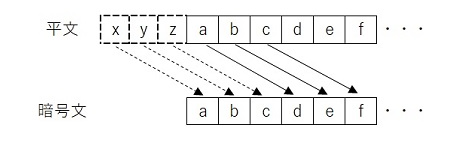
この暗号化手法では、鍵となりうるものが、アルファベットの個数と同じ26個しかない（鍵空間の大きさと呼ばれる）ため、総当りで考えられる鍵をすべて試すことで簡単に暗号を破ることができる。

1.1.2 バーナム暗号

バーナム暗号を、シーザー暗号の拡張と考えると、以下のように書くことができる。

暗号送信者から受信者に対して、後述の量子鍵配送などを用いて乱数を秘密配送する。
次に、送信者は送りたい平文を、配送した乱数を用いて暗号化します。これは実際は作られた乱数と、平文をビットのXOR演算をすることになるが、今回は簡単のためシーザー暗号を用いた。
このときに、送りたい平文が３文字なので、乱数は３つ必要になる。送信者は１文字ずつ、乱数を１つずつ用いて個別に暗号化する。
その後、受信者へと暗号文この場合は、**「PSO」**を送信する。
受信者は、事前にもらった乱数を１つずつ用い、送られてきた**「PSO」を復号し**、メッセージ「DOG」を受け取る。

2. 問題点

シャノンによってその安全性が証明されたが、ワンタイムパッドは実際の運用にゆゆしき難点がある。

乱数は擬乱数ではなく、完全乱数でなければならない。それは容易な要請ではない。完全乱数生成器は存在するが、実際は遅くより専門的である必要がある。
乱数の共有が、完全にセキュアな環境で行われなければならない。仮に攻撃者からこの乱数を傍受された場合、それが認識できなければならない、なぜならこの乱数を知られることにより、攻撃者は送られてくる暗号文を容易に復号できるからである。
使用された乱数はセキュアな形で処分され、それが再利用されるようなことがあってはならないし、発見されて検証されることがあってはならない。

2.1 完全ランダム生成

１に関しては、Linear Congruential-線形合同法やMersenne Twister-メルセンヌ・ツイスタなどといったシードを使った擬ランダム関数を使った手法、つまり
———————————————————–
最初のSEED値を使って第一ランダム数を取得
→第一ランダム数で第二ランダム数を取得
→第二ランダム数で第三ランダム数を取得…
———————————————————–
のような漸化式を使うような手法ではなく、完全ランダムなものを使う必要が有る。ハードウェア乱数生成器などのページを参照してください。

2.2 完全セキュアな乱数共有

２に関しては、量子鍵配送を使うことが解決法となっている。（以下で解説）

2.3 乱数の使い回し防止

３に関しては物理的にメモリの磁気上に保存されたデータを新しいデータで書き換えたり(オーバーライト)、強力な地場を持つデガウザと呼ばれるデバイスを用いて、メモリ上の磁気情報を完全に抹消する(オントラック消去デガウザや、Data Security Inc のデガウザなどをみてみると面白いです。)手法や、もともと保存しておく乱数を暗号化しておくなどの対処を行うことが推奨されている。

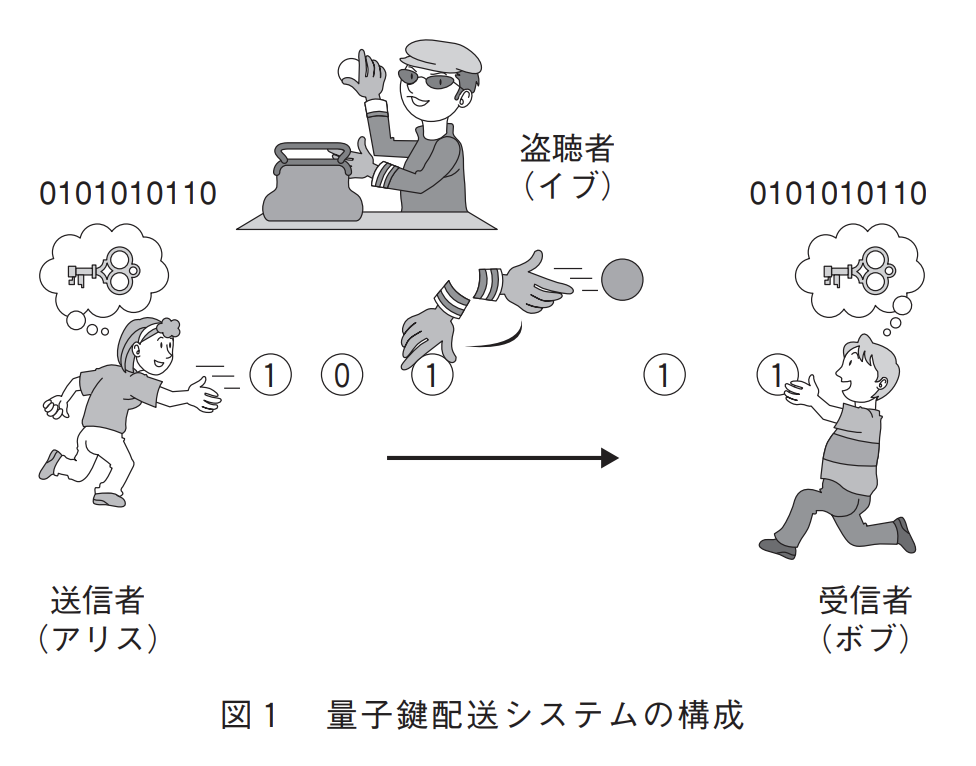
3. 量子鍵配送

NTTからの記事から引用すると、

量子鍵配送(Quantum Key Distribution, QKD)は、量子鍵配送は信頼された２者に対して「暗号鍵」を供給する方式の１つです．量子鍵配送では，量子力学の原理を利用して，盗聴が検知できる通信チャネルを形成し，そのうえで暗号鍵の情報を送受信します．もし，盗聴が検知された場合には，その暗号鍵を破棄して、別のチャネルで再度送付します．ひとたび２者間で安全な暗号鍵が共有できれば，ワンタイムパッド（使い捨て鍵）方式と呼ばれる暗号方式を用いることにより，インターネットなどの通信回線を使って絶対的に安全な暗号通信が可能となります.

とある。

量子鍵配送システムの簡単な構成は、以下である。

引用：NTT技術ジャーナル

この場合、アリスがボブに対して鍵を送る際に、光子と呼ばれる光の粒を用いて鍵ビットを表現する。この際鍵ビットの情報は光の偏向や位相に格納されているが、これらの情報はボブが観測した際に初めて決定する、という量子力学の性質を用いる。光子レベルの信号は、測定操作をすると必ずその痕跡が残る（ハイゼンベルクの不確定性原理）ため、この原理を利用して盗聴を見破ることができる。仮にイブが盗聴をしようとしており、その鍵ビットのうちの１つを観測したとき、ある確率でビット情報が壊れてしまうことを利用することで、盗聴が非常に難しい鍵送信になっている。

3.1 BB84プロトコル

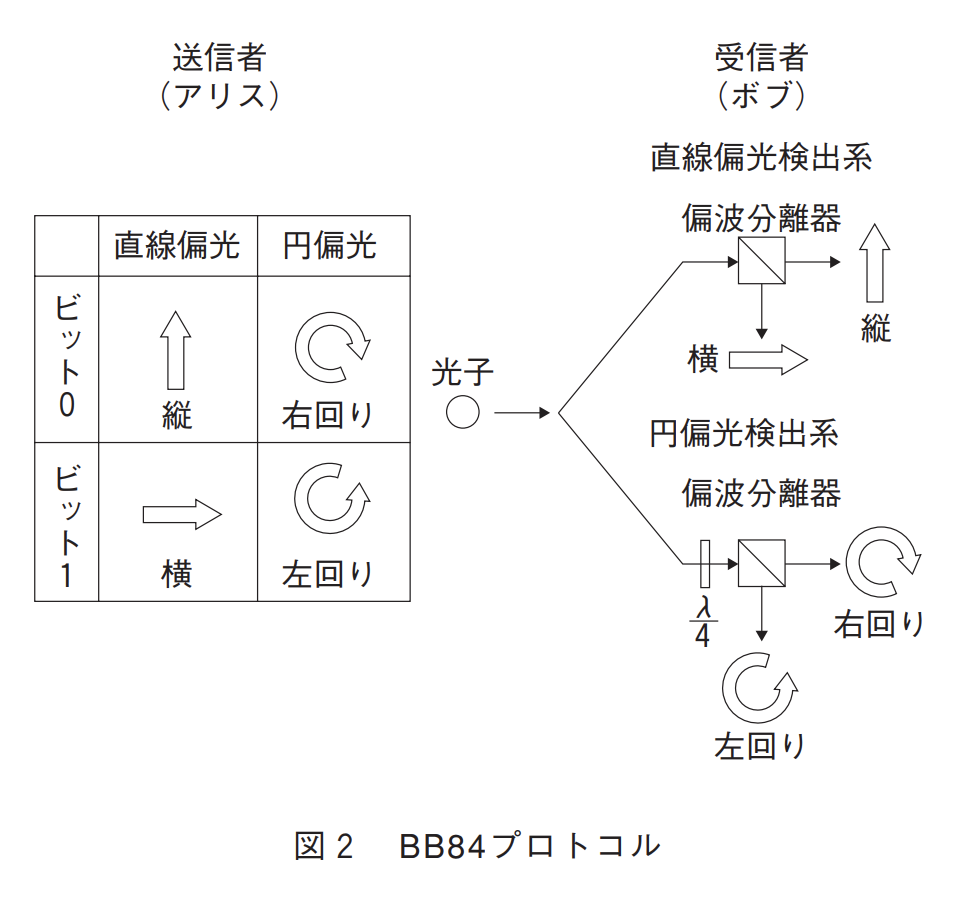
一番有名なのは、BennetとBrassardにより1984年に提案されたBB84プロトコルである。

> 引用：[NTT技術ジャーナル](https://www.ntt.co.jp/journal/0608/files/jn200608049.pdf)

3.1.1 BB84の基本動作

具体的には、上の図のようになる。BB84プロトコルでは，図２のように光子の４つの状態を利用する。ここでは，偏光の縦，横，右回り，左回りの４つを使う。アリスは，上記の４つの状態のうち１つをランダムに選択して，その偏光の光子をボブに送付する。ボブは，４つの状態を同時に判別することはできないため，縦もしくは横が判別できる直線偏光検出系，右回りもしくは左回りが判別できる円偏光検出系のいずれかをランダムに選択して，検出を行う。アリスが，縦もしくは横偏光の光子を送付して，ボブが直線偏光検出系で検出した場合には，偏光状態が判定できる。また、アリスが円偏光の光子を送付し、ボブが円偏光検出系で検出した場合も偏向状態が判定できる。しかし、アリスが直線偏光の光子を送った時に、ボブが円偏光検出系で観測を行った時は、観測ができない。この場合を観測基底が一致しなかった場合、と言う。同様にして、アリスが円偏光の光子を送付したにも関わらず、ボブが直線偏光系で観測を行おうとした時も、どうように観測基底が一致しないので、観測ができない。観測後、ボブはアリスに対してどちらの観測系を用いたかをアリスに伝達し、アリスは観測基底が一致していたかどうかを伝えます。もし、ボブの観測系が、観測基底の一致していない方法だった場合、アリスは今伝達した鍵ビットを破棄し、また送り直す。これにより、５０パーセントの確率で鍵ビットはボブによって観測されるので、十分な数だけこのプロトコルを繰り返すことにより、アリスの鍵ビットは全てボブに送ることができる。

3.1.2 盗聴を試みられた場合

ここで、イブが盗聴しようとした場合を考える。イブの目的は、

送られている鍵ビットを盗み、
かつ盗んだことがアリスとボブにバレないようにすること

である。まず、１を実現するためにイブは偏向の観測をする必要がある。しかしながら、上記での記述通り観測は５０パーセントでしか成功できない。観測基底を当てることのできる確率が５０パーセントだからである。仮に、イブが観測を成功させて、観測したものと同じ偏向のものをボブに送ったとする。このとき、ボブの観測が成功すればイブはこの観測ビットの盗聴に成功する。ただし、ボブの観測が失敗した場合は、アリスによりこの送信はなかったことになるため、イブは盗聴をやり直すことになる。
イブが観測を失敗した場合、イブは５０パーセントの確率でアリスからの偏向を推測し、それをボブに送ることになる。もしイブが推測した偏向が合っていた場合も間違っていた場合も、ボブはいつものように観測プロセスに進むが、仮に間違っていた場合、５０パーセントの確率でそれがボブによりアリスにバレてしまう。もしアリスが自分の送った偏光とボブに届いた偏光が違うことに気づいた場合、アリスは通信が盗聴されていたことを知り、この通信を中断、セキュリティがチェックされた他の通信に切り替えルことができる。これらを繰り返すことで、アリスとボブは盗聴なしに鍵交換ができるというわけです。以上がBB84と呼ばれるプロトコルである。

3.2 研究が進む量子鍵配送

また、最近の記事で、NICTより「国際標準化機関ITU-Tで初の量子鍵配送ネットワークに係る勧告が成立」とあり、NICT、NEC、東芝という日本のトップ企業が、引き続き国内外の企業や研究機関と協力し、QKD技術の研究開発と標準化に取り組んでいます。

おそらく、量子鍵配送は当たり前に使われる技術になっていくでしょう。

4. まとめ

####「バーナム暗号は究極の暗号である」
バーナム暗号をもちいたワンタイムパッドは理論的に完全安全という意味で、とても最適化された暗号である。
さらに、バーナム暗号は巨大な整数を法とした計算や、高次元の格子を用いたりする、ハイパフォーマンスのコンピュータ有りきの暗号と違い、手で運用できる暗号であることも大きなメリットである（仮に上記の問題点をうまく解決することができ、コンピュータの性能が今とは比べ物にならないくらい上がったときに残るのは意外とバーナム暗号かも？？）。
とにもかくにも、バーナム暗号を用いたワンタイムパッドは、２つのパーティがセキュアな同一環境下にあり、そのパーティが２つのセキュアな環境下に別れるとき、とても最適な暗号である。（つまり、問題点の２が解決されるとき。）さらに、この要請は、

「量子鍵配送によって実現される」

量子鍵配送は、日本でもNTT, NEC, 東芝、NICTなど様々な企業が研究をしています。

以上がまとめになります。

今回は、バーナム暗号についてとても面白かったので調べてみました。暗号理論は歴史が深いので、いろいろなエピソードと紐ついていて調べるのが面白いですね。また、裏で働く数学もいろいろなものがあり面白いと思っています。

もし興味深い記事だなと思っていただけたら、「いいね」や「コメント」お待ちしております！！

おわり。

5. 参考文献

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up

暗号解説シリーズ 情報理論の父シャノンでも解けなかった 究極の暗号「バーナム暗号」を解説！！