Python による主成分分析(PCA)と背後の線形代数(SVD)

この記事は， ESM Advent Calendar の 12/12 日です．ESMは株式会社永和システムマネジメントという社名の略です（Ruby やアジャイルで有名 ... なはず）．

現在，「機械学習チーム」を立ち上げて勉強会をやっています．この記事では「勉強会」ネタから，主成分分析(PCA)の回をコードを交えてご紹介します．コードは， Colab にて（そちらが詳しいです）．

この記事は，こちらの Qiita記事 を大いに参考にさせて頂きました．ありがとうございます．

これは何か？

世の中では，よく「文系」「理系」という言葉が使われます．それをうまく PCA(主成分分析）で取り出してみることで，機械学習のコードによって視覚化してみようということです．文系理系という言葉の「是非」はおいておいて，PCAを直感的に分かりやすく解説し，動かしてみよう！という趣旨です．

レベルは初級，PCAを直感的理解したい方(seabornで可視化)，さらに末尾に数学的にSVDとの関係やリンクにSVDの数学を入れました．

利用ライブラリ

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import io
import seaborn as sns

おなじみだと思いますが，今回は seaborn を積極的に使ってみようと思います．

まずデータ

data_string = io.StringIO(
'''\
KOKU,SHA,SU,RI
30,43,51,63
39,21,49,56
29,30,23,57
95,87,77,100
70,71,78,67
...
''')
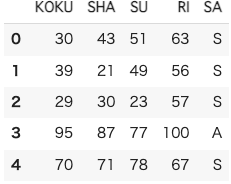
df = pd.read_csv(data_string)

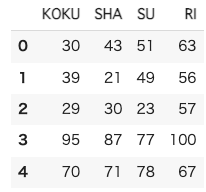
データは参考記事から流用させてもらいました．ただし，説明容易化のために，全データでなく先頭の41データのみです．

df.head()

ちゃんと読み込めているようです．

概況をつかむ

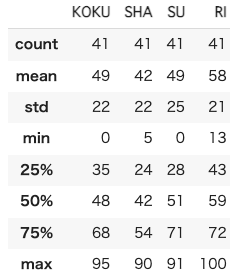
こんな感じで並んでいます．何はなくとも describe してみますか．

pd.options.display.precision = 0
df.describe()

41のデータがあり，平均点は大体40-60くらい．国語と数学には0点がいて，理科には100点がいるね．標準偏差もおなじくらいで，20くらい．ヒストグラム書いてみる．

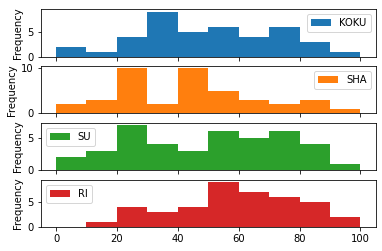
ヒストグラム

df.plot(kind="hist",subplots=True)

• 理科が他より高い
• 社会にふたこぶみえる．他の教科も中高ではない．（データも少ないし）．
• ここでは各教科の相関はわからない．

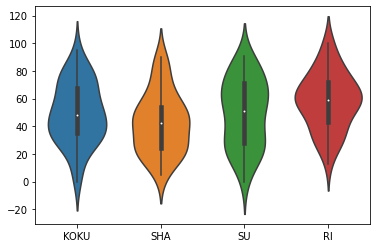
バイオリンプロット

sns.violinplot(data=df)

人気があるので，やってみた（seaborn の violinplot に DataFrame を渡すだけ！)

• 4分位点が表示される（箱ひげ図が内蔵）
• バイオリンプロットだと，曲線で繋ぐので，データが少ない谷間がみえないことがある．
• -20 なんて数字が出てくる．
• これは，記述統計でなく推測統計の場合の母集団がある，と考えたときの推定になっている．（カーネル密度推定）

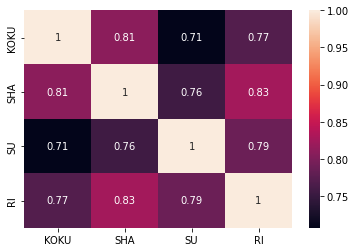
相関

相関見てみる．これも，DataFrameのcorr() で一発で取れる． seaborn のヒートマップを使って可視化．

相関（ヒートマップ）

# 相関係数を計算
correlation = df.corr()
# seabornのヒートマップを使って綺麗に表示
sns.heatmap(correlation, annot=True)

さて，何が言える？何と何の相関が高い？
- 一番高い相関は，社会と理科．（文系理系でない）
- どれも0.7以上（高い）

言いたかったことが見えない．細かくみてみる．

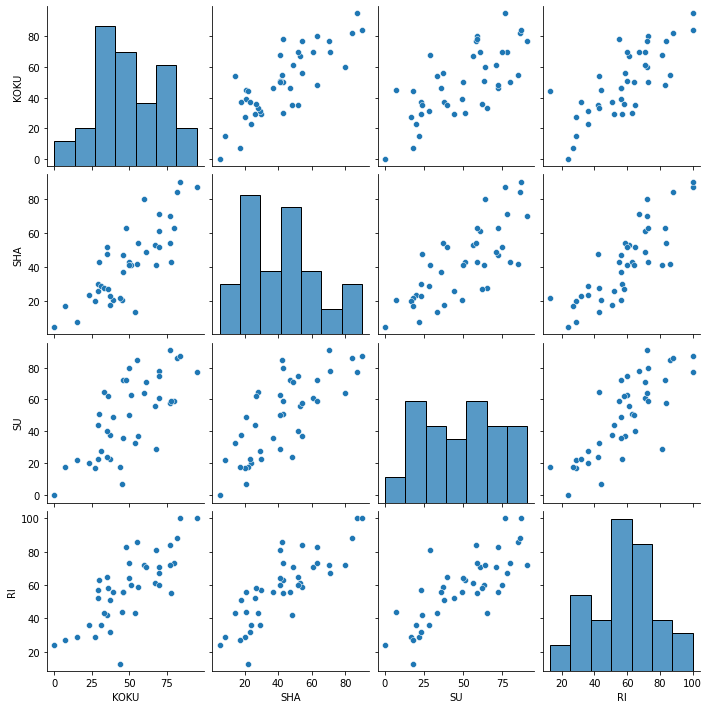
相関（ペアプロット）

ヒートマップだと相関係数を数字と色で表示しているだけだけど，全教科総当たりをプロットしてみる．

sns.pairplot(df)

何が見える？みんな強い正の相関だ．言いたかったことは全然見えてこない．
そこで， PCA の出番ですよ．

PCA(主成分分析)

scikit-learn を使います．

from sklearn.decomposition import PCA

# PCA(主成分分析)
pca = PCA(n_components=2)
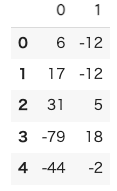
score_feature = pca.fit_transform(df)
pca_df = pd.DataFrame(score_feature)
pca_df.head()

各生徒番号（行番号）ごとに，「国社数理」でなく，「主成分の0と主成分の1」を計算．信号の強い順に2つ取り出したことになる．

PC0(第一主成分), PC1(第二主成分) で散布図書いてみる．

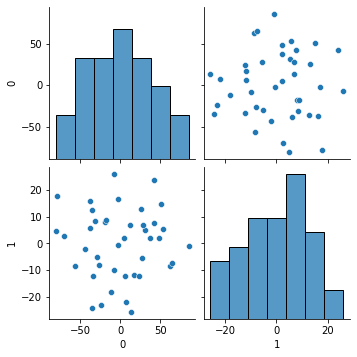
ちらばった（よいこと）．しかし，なんやわかん．

文系・理系仮説

仮説を立ててみる．文系と理系の傾向を出したいので，ラベリングしてみる．

Science と Art(ちなみに，英語でこういう)
- 自然についての学問が Science （理系）
- 人が作ったものについての学問が Art　（文系）

# Art(文系) or Science(理系) ざっくりバージョン
def art_or_science(df):
    return df['KOKU'] + df['SHA'] - df['SU'] - df['RI'] > 0

pca_df['SA'] = df['SA'] = np.where(art_or_science(df), 'A', 'S')

文系理系仮説はどのように言えるのだろう？

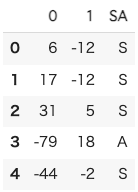
df.head() # 元データの SA
pca_df.head() # PCA の　SA

元データ

PCA

なんとなくだけど，PC1の列，Sがマイナス，Aがプラスになっているように見える．

　可視化は神

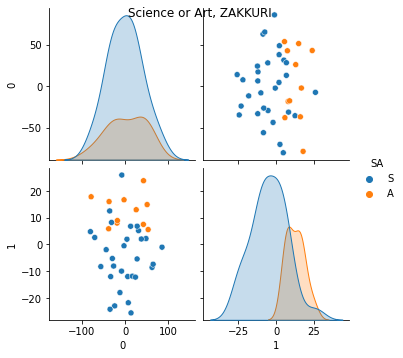
SA のラベルをつけて，ペアプロットしてみる．

わりとはっきりと，PC1 の軸にSAが分離できたようだ．ところで，第一はなんだ？！
当たり前なんですが，ここまで自覚できていなかった．

そう．もともとの点数の高さ．要するに教科によらず，点数の高い人は高いのだ！（これが，最初のプロットですべての教科に強い相関が見られたことを意味している．）

第一の主要因(PC0)の仮説

# 学力の高低をざくり
def high_or_low(df):
  return df['KOKU'] + df['SHA'] + df['SU'] + df['RI'] > 200

df.drop(columns='HL', inplace=True, errors='ignore')
pca_df['HL']=df['HL'] = np.where(high_or_low(df), 'H', 'L')

g = sns.pairplot(pca_df, hue = 'SA')
g.fig.suptitle("Science or Art, ZAKKURI")
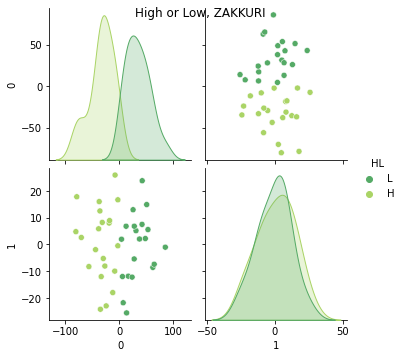
g = sns.pairplot(pca_df, hue = 'HL', palette='summer')
g.fig.suptitle("High or Low, ZAKKURI")

これではっきり見えました．人間の言葉で言うと，「総合学力」と「文系理系」が PC0, PC1 と割とよく対応します．

精度を上げる

各テストの教科ごと難易度とばらつきが違うので，偏差値でやってみる．

# 分離分割をより鮮明になるか？偏差値にする．
def mean_norm(df_in):
    return df_in.apply(lambda x: (x-x.mean())/ x.std(), axis=0)

df.drop(columns='SA', inplace=True, errors='ignore')
df.drop(columns='HL', inplace=True, errors='ignore')

df_std = mean_norm(df.copy())
score_feature = pca.fit_transform(df_std)
pca_df_std = pd.DataFrame(score_feature)

# 調整された AS
def art_or_science_std(df):
  return art_or_science(df)

# 調整された HL
def high_or_low_std(df):
  return df['KOKU'] + df['SHA'] + df['SU'] + df['RI'] > 0

pca_df_std['SA'] = df_std['SA'] = np.where(art_or_science_std(df_std), 'A', 'S')
pca_df_std['HL'] = df_std['HL'] = np.where(high_or_low_std(df_std), 'H', 'L')

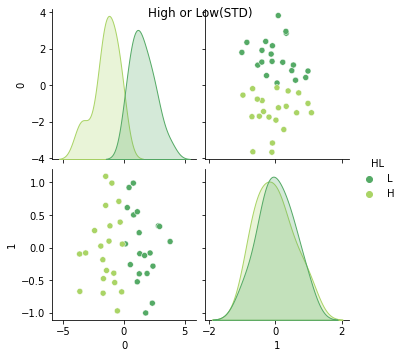
g = sns.pairplot(pca_df_std, hue = 'HL', palette='summer')
g.fig.suptitle("High or Low(STD)")
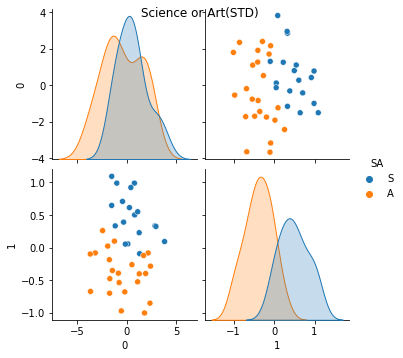
g = sns.pairplot(pca_df_std, hue = 'SA')
g.fig.suptitle("Science or Art(STD)")

おお，よりシャープに，文理を分離できた！あくまでLH, SAは人間がつけたラベルであることに注意．PC0,PC1の本当の意味は純粋にデータ的．

寄与率と固有ベクトル成分

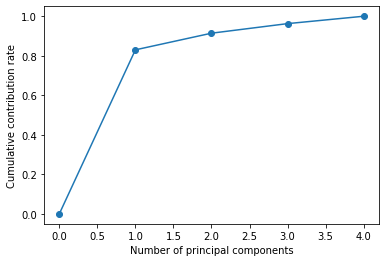
PC0,1,2,3全体の寄与率を求めて，そのくらい PC0, PC1 で全情報をカバーできているかみてみる．

# 今度は第4コンポーネントまで（すべて）
pca=PCA(n_components=4)
score_feature = pca.fit_transform(df)

# 累積寄与率を図示する（足切りしないように，0を追加した)
plt.plot([0]+list( np.cumsum(pca.explained_variance_ratio_)), "-o")
plt.xlabel("Number of principal components")
plt.ylabel("Cumulative contribution rate")

PC0, PC1 を足して，9割！ そして， PC0 で8割超え．．．．学力軸が強く，文系理系はそれにくらべると微々たるもの．

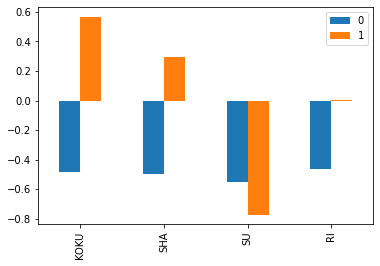
次に，学力(PC0)と文系理系(PC1)それぞれの「国社数理成分」（固有ベクトル）を見てみる

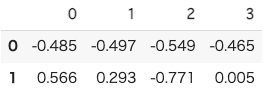
df_components = pd.DataFrame(pca.components_[0:2]);
df_components.columns=['KOKU', 'SHA', 'SU', 'RI'];
df_components.T.plot(kind='bar')
df_components

• PC0 はマイナス方向に満遍なく各教科の混合点数．（PC0は数値が低い方が学力が高い)
• PC1 は国社を高く含み，逆方向に数学．実は，理科は中立．（おもしろい）

まとめ

ぼくが思う重要な結論は，

• 実はもっとも情報量の多い PC0 は「学力」に対応していた．（これで8割説明がつく）
• 次に文系理系とよく似た対応の特徴が現れる．
• 統計学からの反論を以下に．

社外の別の勉強会（動画で学ぶデータサイエンス）でこれを見せたところ，統計学からの反論があった．

• ふたこぶが見えたら，何か隠れた因子を疑うべき．再調査が必要．例えば性別．
• 今回の目的が母集団が持つ決定要因を探ることであれば，再調査にもどってやる．

ほんの少し数学

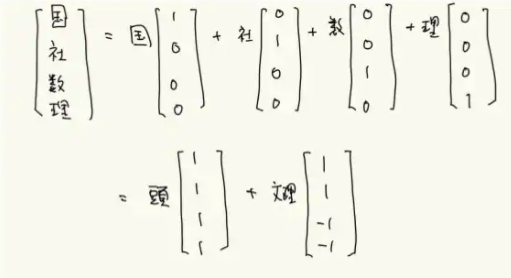
行列の見方と PCA の意味．

行列の掛け算には２つの見方があります．この下の方の見方を身につけると，PCA（SVD）がやっていることの意味が掴めると思います．

4つの軸（国社数理）で表現されるのがフルの情報なんですが，それを「学力」と「文理」の二つの数で表せば，かなりの情報が拾えていることになります．（上位２つの累積寄与で90%越え）　

ただし，2つの固有ベクトル(PC0, PC1)は，簡単のために(1,1,1,1)と(1,1,-1,-1)としましたが，実際の値は，(-0.485,-0.497,-0.549,-0.465), (0.566,0.293,-0.771,0.005)です．

今日は，記事が長くなってしまったので，詳しくは，この資料を．
今回のテーマに沿って，PCAの数学を紹介しています．

（おしまい）