主成分分析(PCA)で文系/理系要素を抽出する

　生徒の成績データを使って、

「文系/理系の存在を証明」

してみたい。

ライブラリ


import numpy as np
import pandas as pd
import  matplotlib.pyplot as plt
import seaborn as sns
from sklearn.decomposition import PCA

データセット

・東京大学森純一郎先生の授業「データマイニング入門」で使ったものを使わせていただいています。
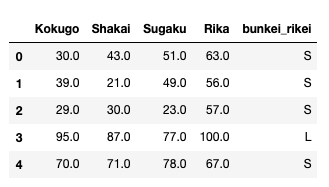
・データ"exam_score"は以下のように、国語、社会、数学、理科を列にもつ、166x4のデータです。

## exam_score.csvファイル
kokugo, shakai, sugaku, rika
30, 43, 51, 63
39, 21, 49, 56
...

データを読み込み、DataFrame化します。

文系科目 = 国語と社会
理系科目 = 数学と理科

とし、国語 + 社会 - 数学 - 理科の点数が非負 or 負で文系と理系をラベル付けしました。

# csvファイルからNumPy配列の作成
score = np.loadtxt("exam_score.csv", delimiter=",", skiprows=1)
df = pd.DataFrame(score, columns=['Kokugo','Shakai','Sugaku','Rika'])
# 文系=L / 理系=S
df['bunkei_rikei'] = np.where(df['Kokugo'] + df['Shakai'] - df['Sugaku'] - df['Rika'] >=0, 'L', 'S')
df.head()

これで前準備は完了です。それでは分析を始めます!

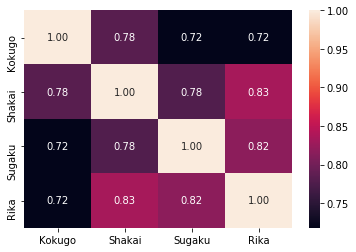
各変数間の相関係数をみる

　各変数間の相関係数をseabornのヒートマップを使って可視化してみます。文系科目 (国語・社会) と理系科目 (数学・社会) で相関がどうなっているのかに注目してください。

# 相関係数を計算
correlation = df.corr()
# seabornのヒートマップを使って綺麗に表示
# annot: annotationの略。値を表示するかどうか
# fmt: プロットのフォーマットを設定。'.2f'で小数点以下2桁まで
sns.heatmap(correlation, annot=True, fmt='.2f')

・理系科目(数学・理科)同士の相関は比較的高い。
・国語と理系科目の相関係数は、国語と社会との相関係数より確かに少し低い。

だが、

・上記の2点でそれほど有意な差があるとは思えない。
・文系科目である社会と理系科目である理科の相関係数が一番高い。

となり、結局、単に「文系/理系の区別などなく、頭の良い人は全ていい点数を取るのでは?」という結論に達してしまうようです。

そこで今度は主成分分析を行ってみることにします。

主成分分析

　主成分分析はデータを説明する本質的なベクトルを抽出することで、次元削減を行う手法です。つまり、データを要約することができます。今回は各科目の4次元のデータを2次元に圧縮します。その過程で、文系/理系を表す軸が出てこないかを期待します。

X = score
# 主成分を2つまで取得
pca = PCA(n_components=2) 
X_pca = pca.fit_transform(X)

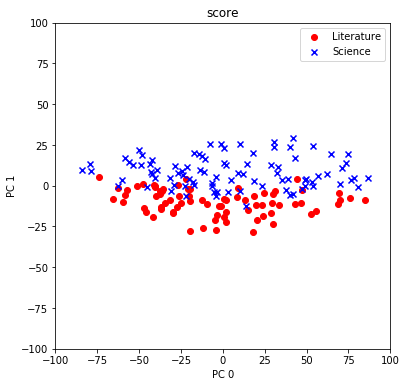
# 特徴抽出による可視化
# PC0(第1主成分)とPC1(第2主成分)について散布図を表示
plt.figure(figsize=(6, 6))
# 文系と理系で色と点を変えてプロット
for target, marker, color in zip('LS', 'ox', 'rb'):
    plt.scatter(X_pca[df['bunkei_rikei']==target, 0], X_pca[df['bunkei_rikei']==target, 1], marker=marker, color=color)

plt.xlim([-100, 100])
plt.ylim([-100, 100])
plt.title('score')
plt.xlabel('PC 0')
plt.ylabel('PC 1')

　青いxでプロットされたのが理系で赤丸でプロットされたのが文系です。どうやら第2主成分(PC1)が文系/理系を区別する主成分になっているようです! 寄与率と因子負荷量を出すことで、もう少し詳細にみていきましょう。

寄与率

# 寄与率を出力
# [第1主成分の寄与率 第2主成分の寄与率]
print(pca.explained_variance_ratio_)

[0.83141975 0.07912514]

因子負荷量

# 因子負荷量を出力
# ['Kokugo, 'Shakai, 'Sugaku', 'Rika']
pca.components_ * np.sqrt(pca.explained_variance_)[:, np.newaxis]

array([[19.11790816, 19.86989087, 22.32458143, 19.74611605],
[-9.68917951, -1.87915453, 6.87063499, 3.50405057]])

結果の解釈

寄与率について

　第1主成分が80%以上の説明力を持っています。それに比べて、僕が文系/理系のシグナルと睨んだ第2主成分の寄与率は約8%とかなり微弱ですね。

因子負荷量について

第1主成分

第1主成分は

[Kokugo, 'Shakai, 'Sugaku', 'Rika']

= [19.11790816, 19.86989087, 22.32458143, 19.74611605]

となっており、教科間でほとんど差がありませんね。これは生徒の「地頭の良さ」を表すものだと解釈してしまってよいと思います。やはり地頭の良さは数学に出るようですね。

第2主成分

第2主成分は

[Kokugo, 'Shakai, 'Sugaku', 'Rika']

= [-9.68917951, -1.87915453, 6.87063499, 3.50405057]

となっており、国語・社会ではマイナスの値が、数学・理科ではプラスの値が出ています。特に絶対値に注目すると、マイナスは国語が、プラスは数学の値が大きいです。この第2主成分は 「理系らしさ」を数値化していると言って良いのではないでしょうか?

結論

　寄与率を見ると、第1主成分が支配的で80%以上を占めています。ですから、「文系/理系」というのは「地頭の良さ」を前にしては、

　ほとんど無きに等しい (定量的には地頭の良さの1/10程度)

　といえます。しかし、微弱なシグナルだが主成分分析をもってすれば確かに

「文系/理系が存在すること」を証明することができる

　ようです。おそらくこの基準にしたがって分類器を作成することも可能でしょう。