これはNTTドコモ R&D控え室 アドベントカレンダー、16日目の記事です。 今年も各国の金融緩和や大統領選挙など、いろいろなことがありましたね。この記事では様々な資産(アセット)のデータ分析を通して、2020を振り返ってみたいと思います。
TL; DR
- 株指数や債券、商品のデータを取得して、年初来リターンなど基本的な分析を行うよ😃
- クラスター分析を通じて、2020年のアセット間の結びつきを分析するよ🤔
- ポートフォリオ最適化によって、2020年で成績がよくなったポートフォリオを観察するよ👀
※ 本記事は投資を斡旋するものではなく、結果を用いた損失に対して責任を持たないよ!
はじめに
今回の分析はPythonで行います。
まず、利用するライブラリをインポートしておきます。
import pandas as pd
import numpy as np
import datetime
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
# クラスター分析で利用
from sklearn import cluster, covariance, manifold
# ポートフォリオ選択で利用
from pypfopt.efficient_frontier import EfficientFrontier
from pypfopt import expected_returns
from pypfopt import risk_models
from pypfopt import CLA
from pypfopt import plotting
データ取得
分析対象とする、各アセットのデータを取得します。今回は金融データをまとめサイトのstooqで使えるAPIを利用します。
各アセットのstooqのページで、URL情報を確認しながら取得対象のアセットに関する辞書を作成します。例えばGOLDのstooqのアドレスは
であり、 xauusd がパラメータとなっています。順に確認しながら、下記のような辞書を作成しました。
symbol_dict = {
'%5Espx':'S&P500',
'%5Edji':'DJI30',
'%5ENKX':'NI225',
'%5Etpx':'TOPIX',
'agg.us':'AGG',
'2510.jp':'2510',
'xauusd':'GOLD',
'btcusd':'BTC',
'iyr.us':'IYR',
'%5Endq':'NASDAQ',
'cl.f':'WTI',
'2042.jp':'Mothers',
'xagusd':'Silver'
}
辞書には代表的と思われる株指数や債券、商品(コモディティ)を含めてみました。
| 名称 | カテゴリ | 説明 |
|---|---|---|
| S&P500 | 株 | アメリカの代表的な株価指数. ニューヨーク証券取引所などに上場されている500銘柄から構成 |
| DJ30 | 株 | Tダウ平均株価, S&P500同様に代表的な株価指数。30銘柄から構成 |
| NASDAQ | 株 | NASDAQに上場されている銘柄の時価総額加重平均で算出した株価指数 |
| TOPIX | 株 | 東証第一部上場株の時価総額の合計を終値ベースで評価した株価指数 |
| NKI225 | 株 | 東証第一部上場銘柄のうち流動性の高い225銘柄によって構成される株価指数 |
| Mothers | 株 | 日本の新興市場 |
| AGG | 債券 | BlackRockの米国債券ETF |
| 2510 | 債券 | 野村證券による国内債券ETF |
| IYR | 不動産 | BlackRockの米国不動産ETF |
| GOLD | 商品 | 貴金属の代表 |
| Silver | 商品 | GOLD同様、貴金属の代表的な資産 |
| BTC | 商品 | 暗号資産の代表。2008年に誕生 |
| WTI | 商品 | アメリカの代表的な現有先物 |
作成したアセットのデータを取得します。後の分析のため、各アセットが共通して取引された日時に限定しデータセットを作成します。
symbols, names = np.array(list(symbol_dict.items())).T
df = pd.read_csv(f'https://stooq.com/q/d/l/?s={symbols[0]}&i=d',index_col=0)
df.index = pd.to_datetime(df.index).tz_localize('Asia/Tokyo')
df['variance'] = df['Close'] - df['Open']
df = df[['Close', 'variance']].copy()
df.columns = [names[0], names[0] + '_variance']
for i in range(1, len(symbols)):
temp_df = pd.read_csv(f'https://stooq.com/q/d/l/?s={symbols[i]}&i=d',index_col=0)
temp_df.index = pd.to_datetime(temp_df.index).tz_localize('Asia/Tokyo')
temp_df['variance'] = temp_df['Close'] - temp_df['Open']
temp_df = temp_df[['Close', 'variance']].copy()
temp_df.columns = [names[i], names[i] + '_variance']
# Dateをキーにして順次データを突合
df = df.merge(temp_df, on = 'Date', how = 'inner')
下記のようなデータが作成できました。
| S&P500 | S&P500_variance | DJI30 | DJI30_variance | NI225 | NI225_variance | ... | WTI | WTI_variance | Mothers | Mothers_variance | Silver | Silver_variance | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Date | |||||||||||||
| 017-12-11 00:00:00+09:00 | 2659.99 | 7.8 | 24386.03 | 47.92 | 22938.73 | 44.43 | ... | 57.99 | 0.74 | 12950 | 160 | 15.7125 | -0.137 |
| 2017-12-12 00:00:00+09:00 | 2664.11 | 2.38 | 24504.8 | 51.84 | 22866.17 | -70.24 | ... | 57.14 | -0.88 | 12870 | -70 | 15.738 | 0.0075 |
| 2017-12-13 00:00:00+09:00 | 2662.85 | -4.74 | 24585.43 | 60.24 | 22758.07 | -112.26 | ... | 56.6 | -0.85 | 12930 | 10 | 16.08 | 0.3445 |
| 2017-12-14 00:00:00+09:00 | 2652.01 | -13.86 | 24508.66 | -122.35 | 22694.45 | -4.85 | ... | 57.04 | 0.34 | 13050 | 120 | 15.8975 | -0.1745 |
| 2017-12-15 00:00:00+09:00 | 2675.81 | 15.18 | 24651.74 | 66.03 | 22553.22 | -68.14 | ... | 57.3 | 0.15 | 12960 | -40 | 16.0525 | 0.155 |
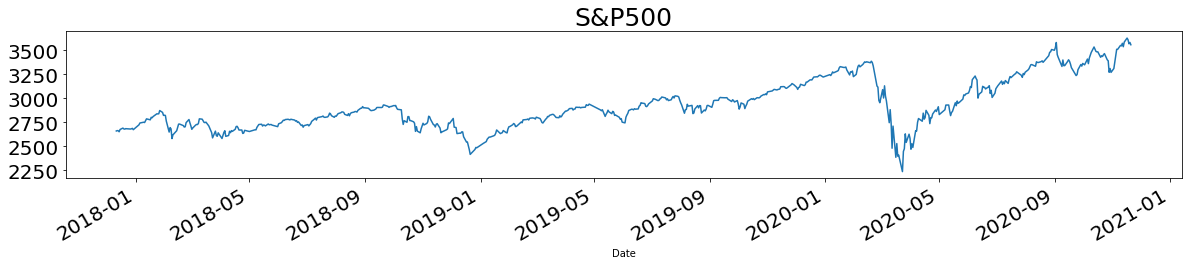
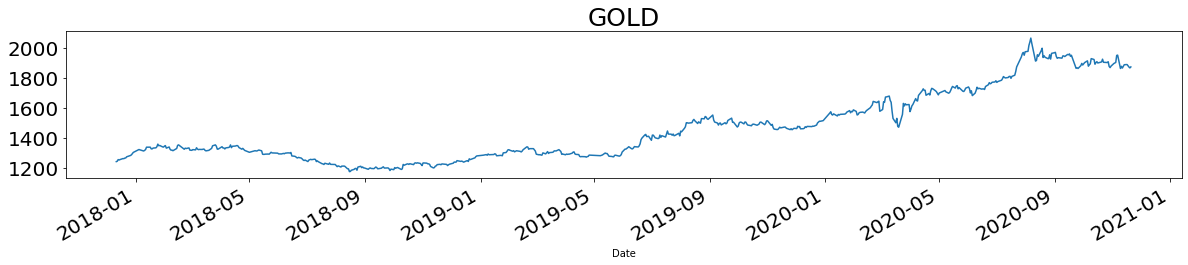
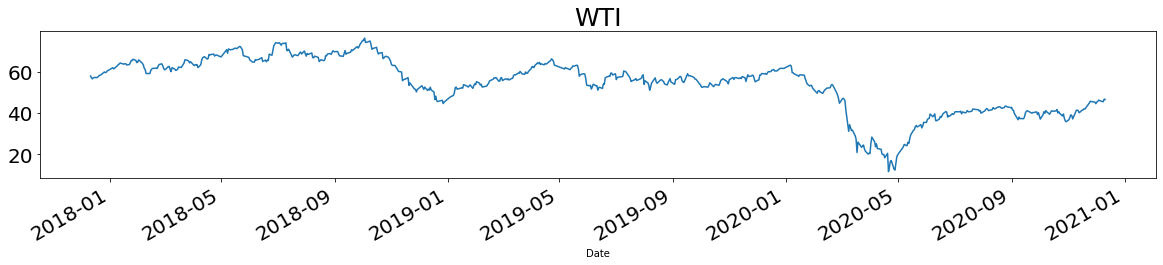
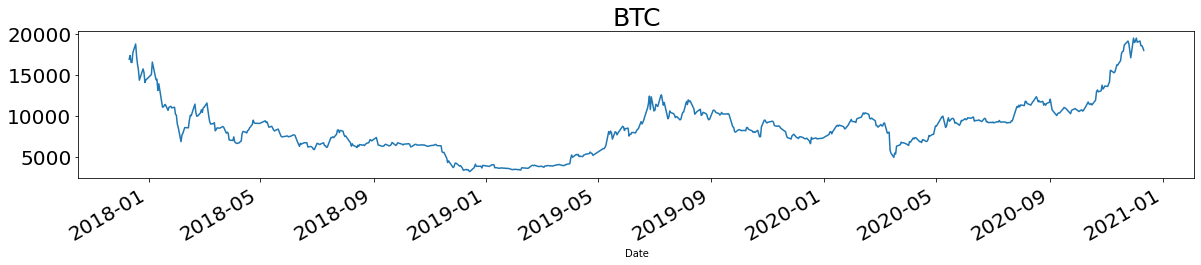
取得したデータを時系列で可視化します(ここではいくつかをピックアップして表示)。
for name in names:
plt.title(name, fontsize=25)
df[name].plot(figsize = (20,3), fontsize = 20)
plt.show()
基礎分析
取得したデータを元に、基礎的な分析を行います。
計算しておいた差分系列(カラム名の末尾が_varianceとなっているもの)を元に、2020年における正になっている数(陽線)と負になっている数(陰線)の数を比較してみます。
df_var = df['2020'].iloc[:, df.columns.str.endswith('e')]
a_df = pd.DataFrame(df_var[df_var > 0].count(), columns = {'positive'})
b_df = pd.DataFrame(df_var[df_var < 0].count(), columns = {'negative'})
posinega_df = pd.merge(a_df, b_df, left_index=True, right_index=True)
計算したposinega_dfの中身は次の通りです。
| positive | negative | |
|---|---|---|
| S&P500_variance | 129 | 93 |
| DJI30_variance | 118 | 104 |
| NI225_variance | 107 | 115 |
| TOPIX_variance | 111 | 111 |
| AGG_variance | 102 | 113 |
| 2510_variance | 77 | 88 |
| GOLD_variance | 127 | 95 |
| BTC_variance | 119 | 100 |
| IYR_variance | 106 | 116 |
| NASDAQ_variance | 129 | 93 |
| WTI_variance | 105 | 113 |
| Mothers_variance | 111 | 105 |
| Silver_variance | 117 | 100 |
差分系列においてプラスなら陽線、マイナスなら陰線と言えます。この結果から、陽線の数はS&P500、GOLD、NASDAQの順に多かったことがわかります。また陰線の数はNI225、WTI、TOPIXの順に多かったことがわかります(ただし全てのアセットが取引できた日に限定)。
次に年初来リターン、最安値リターン、変動係数を定義し計算します。
- 年初来リターン:昨年末の資産価格に対する現在の価格の増加率。ここでは計算を簡単にするために、昨年末の価格と年初の価格はほぼ同じと仮定し、ある年のあるアセットにおける価格時系列を$X = x_i(i =0,1,2,..., N)$として$ x_N/x_0$で年初来リターンを定義します。
- 最安値リターン:各年の最安値時に購入した場合のリターン。$ x_N/min(X)$で定義します。
- 変動係数:アセットごとの標準偏差を平均値で割ったもの。ある年の標準偏差を$\sigma$, 平均値を$m$として$\sigma/m$で定義します。
result = []
for year in ['2018', '2019', '2020']:
for name in names:
year_df = df[name][year]
return_start = year_df[-1]/year_df[0]
return_min = year_df[-1]/np.min(year_df)
variation_cof = np.std(year_df)/np.mean(year_df)
result.append([year, name,return_start, return_min, variation_cof])
result_df = pd.DataFrame(result)
result_df.columns = ['year', 'name', 'return_start', 'return_min', 'variation_cof']
# 年初来リターンランキング
display(result_df.loc[result_df['year'] == '2020']
.sort_values('return_start', ascending = False)
[['name', 'return_start']].reset_index(drop = True).head(10))
# 最安値リターンランキング
display(result_df.loc[result_df['year'] == '2020']
.sort_values('return_min', ascending = False)
[['name', 'return_min']].reset_index(drop = True).head(10))
2020年における年初来リターンランキングは
| ランキング | name | return_start |
|---|---|---|
| 1 | BTC | 2.329704 |
| 2 | NASDAQ | 1.364484 |
| 3 | Mothers | 1.351522 |
| 4 | Silver | 1.320110 |
| 5 | GOLD | 1.174844 |
| 6 | NI225 | 1.148575 |
| 7 | S&P500 | 1.128510 |
| 8 | AGG | 1.059420 |
| 9 | TOPIX | 1.049791 |
| 10 | DJI30 | 1.046789 |
また最安値リターンランキングは
| ランキング | name | return_min |
|---|---|---|
| 1 | WTI | 4.025065 |
| 2 | BTC | 3.641177 |
| 3 | Mothers | 2.153846 |
| 4 | Silver | 2.004266 |
| 5 | NASDAQ | 1.804178 |
| 6 | S&P500 | 1.637374 |
| 7 | DJI30 | 1.616097 |
| 8 | NI225 | 1.610149 |
| 9 | IYR | 1.485980 |
| 10 | TOPIX | 1.441359 |
最後に、変動係数ランキングは
| ランキング | name | variation_cof |
|---|---|---|
| 1 | BTC | 0.298883 |
| 2 | WTI | 0.256571 |
| 3 | Silver | 0.213790 |
| 4 | Mothers | 0.209597 |
| 5 | NASDAQ | 0.137999 |
| 6 | S&P500 | 0.096200 |
| 7 | NI225 | 0.095807 |
| 8 | IYR | 0.095198 |
| 9 | DJI30 | 0.091650 |
| 10 | GOLD | 0.079408 |
となりました。2020年の年初来リターンが最も良かったのはBTC、2番目に良かったのはNASDAQ、3番目に良かったのはMothersでした。陽線の本数が多かったS&PやGOLDが上位に来るように思われますが、反しているのが面白いですね。
最安値リターンが最も良かったのはWTI、次いでBTC、Mothersでした。今年は原油が一時期マイナス圏まで到達したのが印象に残っています1。一方でこれらのアセットは変動係数ランキングでも上位であり、値動きも激しかったことがわかります。
クラスター分析
各アセット同士がどのような相関を持ち、どのようなクラスター構造に分かれるかを分析します。
クラスター分析にはGraphical Lassoを用います。この手法では、ガウシアングラフィカルモデルにおける精度行列をスパース推定し、変数間の関係性を抽出します。今回は時系列を一定期間ごとに区切り、各期間におけるクラスターを分析します。
# 期間の単位
unit = 10
cluster_df = pd.DataFrame(np.zeros((len(names), len(names))))
cluster_df.columns = names
cluster_df.index = names
variance_arr = np.array(df_var.T)
for j in range(0, int(len(variance_arr.T)/unit)):
temp_variance = []
for i in range(0,len(variance_arr)):
temp_variance.append(variance_arr[i][unit*j:unit + unit*j])
temp_variance = np.array(temp_variance)
# クラスターを計算
edge_model = covariance.GraphicalLassoCV()
X = temp_variance.copy().T
X /= X.std(axis=0)
edge_model.fit(X)
_, labels = cluster.affinity_propagation(edge_model.covariance_)
n_labels = labels.max()
# 後のヒートマップ可視化で使うdataframeを生成(cluster_df)
for i in range(n_labels + 1):
print('Cluster %i: %s' % ((i + 1), ', '.join(names[labels == i])))
for j in range(0 ,len(names[labels == i])):
for k in range(j ,len(names[labels == i])):
A = names[labels == i][j]
B = names[labels == i][k]
cluster_df[A][B] = cluster_df[A][B] + 1
例えばある期間におけるクラスタは下記のように分かれます。
Cluster 1: S&P500, DJI30, IYR, NASDAQ
Cluster 2: NI225, TOPIX
Cluster 3: AGG, 2510, GOLD, BTC, WTI, Mothers, Silver
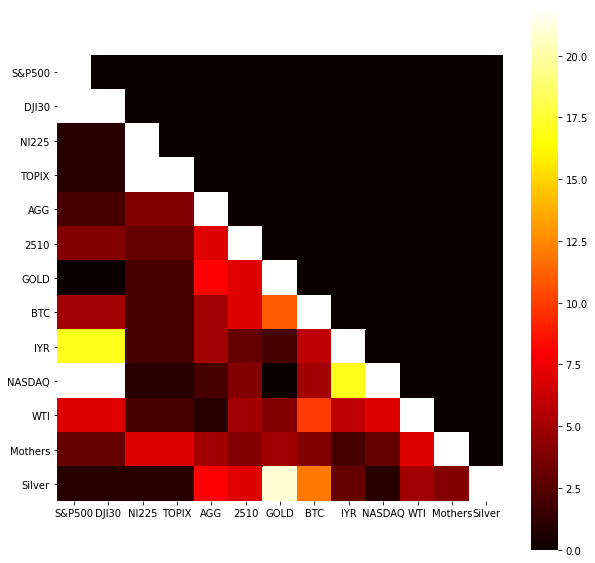
ここで2020年の各期間で同一クラスターと判定された回数をcluster_dfに計算過程で格納したので、ヒートマップで可視化してみましょう。
plt.figure(figsize=(10, 10))
sns.heatmap(cluster_df, cmap='hot', square=True)
S&P500はDJ30、IYR、NASDAQと、NI225はTOPIXと, GOLDはSILVERと高い頻度で同一クラスターに属していたことがわかります。それぞれアメリカのアセット、日本のアセット、貴金属というように分かれていて、わかりやすい結果ですね。一方でWTIやMOTHERS, BTC及び債券は特定のアセットと常に動きをともにしていた訳ではないことがわかりました。
ポートフォリオ最適化
最後にポートフォリを最適化を通じて、2020年において良いリターンとなったポートフォリオを振り返ります。
資産を各々一定の比率で持った構成をポートフォリオとよび、ある数理的な基準に基づいてその比率を決定することをポートフォリオ最適化と呼びます。
現代ポートフォリオ理論では、ある期待収益率を達成するポートフォリオの中で、最も収益率の分散(リスク)が最も小さくなるものを選択するとします。
すなわち$i$を資産、$\omega$を資産配分、$R$をリターンとして
$${\rm min}, \sigma ^2$$
$${\rm subject, to}, \Sigma^n_{i = 1}E(R_i)\omega_i = \mu_p, \Sigma^n_{i = 1} \omega_i = 1$$
の最適化問題を解きます。この時得られる曲線を効率的フロンティアと呼びます。
今回のポートフォリオ最適化には、pyPortFolioOptというライブラリを用います。
https://pyportfolioopt.readthedocs.io/en/latest/
PyPortFolioOptにはいくつかのリターン、リスクモデルが実装されています。今回は期待リターンのモデルとして過去のリターンの指数加重平均を用いるema_historical_return、リスクモデルとして指数加重共分散を採用するexp_covを用います。
# https://github.com/robertmartin8/PyPortfolioOpt を参考
pf_df = df.loc[:, ~df.columns.str.endswith('e')]['2020'].copy()
returns = pf_df.pct_change().dropna()
# 期待収益モデルの計算
mu = expected_returns.mean_historical_return(pf_df)
# リスクモデルの計算
S = risk_models.sample_cov(pf_df)
# Crticial Line Algorithm
cla = CLA(mu, S)
print(cla.max_sharpe())
cla.portfolio_performance(verbose=True)
# 効率的フロンティアを可視化
plotting.plot_efficient_frontier(cla)
出力結果は
OrderedDict([('S&P500', 0.0), ('DJI30', 0.0),
('NI225', 0.0), ('TOPIX', 0.0), ('AGG', 0.26939262357400917),
('2510', -9.94981904377823e-17), ('GOLD', 0.0),
('BTC', 0.5073487323690984), ('IYR', 0.0), ('NASDAQ', 0.0), ('WTI', 0.0), ('Mothers', 0.22325864405689239), ('Silver', 0.0)])
Expected annual return: 103.2%
Annual volatility: 38.6%
Sharpe Ratio: 2.62
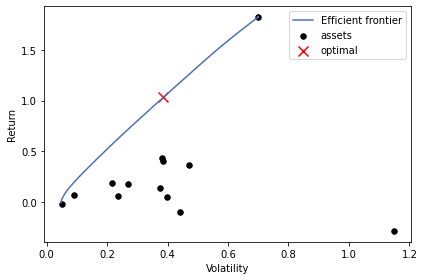
となりました。今回はポートフォリオとしてBTCを51%、AGGを27%、Mothersを22%持つと良いという結果になりました。またこの時、年間リターンが103%, shart rationが2.62という結果になりました。計算された効率的フロンティアは下図になります。
赤いバツマークが今回の最適解とみなされたポイントです。最上部に位置しているassetsはBTCですが、これが曲線に大きな影響を与えています。BTCを除くと、もう少しまともな年間リターンになります。興味がある人は試して見てください📃
まとめ
今回は代表的なアセットのデータを取得し、基礎分析やクラスター分析、ポートフォリオ分析などを通して2020のマーケットを振り返ってみました。クリスマスまで、残りのアドベントカレンダーもお楽しみください🎄
参考
- pythonで日本株の株価を取得してローソク足の描画
- marketneutral/pairs-trading-with-ML
- GraphLassoによる変数間の関係のグラフ化
- グラフィカル LASSO
- PyPortfolioOptでポートフォリオ最適化
- 効率的フロンティアとは?最適なポートフォリオを考えてみよう!
- 現代ポートフォリオ理論
-
この時期にWSJ面白かった記事。保管された原油は今どうなっているのかな。https://jp.wsj.com/articles/SB12076302647651404700904586378814274551684 ↩