PythonでやるML Cycle2: 多項式回帰で未来を予測する

機械学習の教師あり学習の代表格 回帰 について学びます。PRML上巻の序論にある多項式フィッティングの内容です。

ゴール

• 線形・多項式回帰を数学的に理解して実装する。

モチベーション

説明

以下のようなシチュエーションで回帰を考えてゆきます。

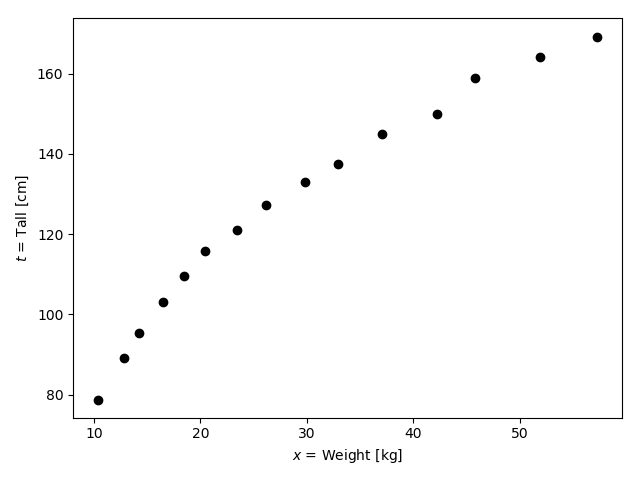
1歳から15歳までの子どもグループ15人でお揃いのユニフォームを作ります。ユニフォームを作る仕立て屋さんは、15人を一つの部屋に集めて、それぞれの体重と身長を測定しました。以下はそれをプロットしたものです。(このデータは厚生労働省が公開している身体状況調査の中の、1歳から15歳の体重と身長の平均をそれぞれ取ったものです。)

実際のデータは以下のようになっていました。

Tall,Weight
78.8,10.4
89.1,12.8
95.3,14.2
103.2,16.5
109.5,18.5
115.9,20.4
121.1,23.4
127.3,26.2
133.1,29.8
137.5,32.9
145,37.1
149.9,42.2
158.8,45.8
164.1,51.9
169.2,57.2

さて、このグループに16人目がやってくるそうです。身長はわかりませんが、体重は35.6kgということだけわかりました。仕立て屋さんは、今のうちにどれくらいのサイズのユニフォームを準備しておくべきか、見当をつけておきたいと思いました。

問題です: 仕立て屋さんは、16人目の子の身長を何cmと予測できるでしょうか？

この問題に答えようとすると、まず2cmや500cmという回答はしないでしょう。人間らしい妥当な身長を考えたいです。では、体重35kgくらいというのは、身長およそどれくらいなのかな？と考えます。

この上で、既に計測してしまっている15人のデータを見てみましょう。おそらくこのデータを見ながら次のような回答を考えるのではないでしょうか: 「以前に測った子だと、32kgで137cm, また37kgで145cmだった。ということは35.6kgということは大体140㎝付近かな」

もちろん、この回答が正しい確証はありません。あくまで予測です。実際は身長160cmの超やせ型の子が来るかもしれません。しかし、体重しか情報がない今、上記のように考えることは合理的ではあるでしょう。そして私たちも日常的にやっている思考です。

このアバウトな回答の導きをプログラムにやらせよう、というのが今回のモチベーションです。

線形回帰を理解して実装する

説明

ではプログラムこれを実現させる具体的な方法を考えていきます。

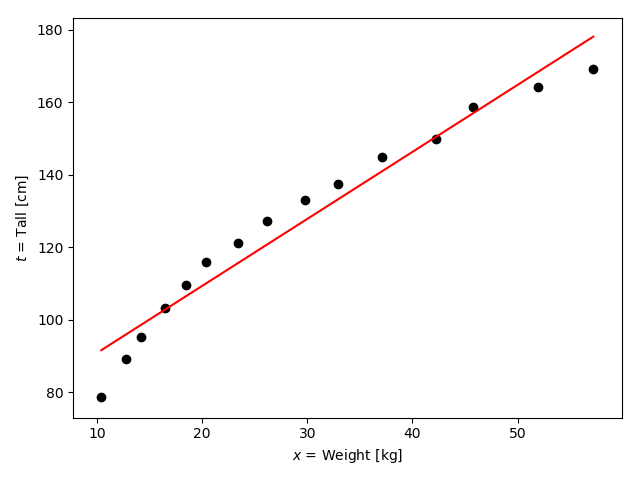
まず以下の図を見てください。

特に赤い直線に注目します。この直線は、●点の間を縫って引かれているように見えますね。

今度はこの直線を$x$と$t$の一次関数と捉えてみます。

y(w_0, w_1, x) = w_0 + w_1 x

もし、この一次関数の$w_0, w_1$の値がわかったとしたら、$x$に体重を代入すれば、計算した結果の$y(x)$として、私たちが得たいアバウトな身長が得られると思いませんか？

このアイディアを一般に回帰と呼び、この赤い直線のような関数$y(x)$を得ることを関数$y(x)$に回帰すると言ったりします。また、今回のように直線(=一次関数)に回帰させることを特に線形回帰と呼び、n次関数($n \geq 2$)に回帰させることを多項式回帰と呼びます。

実際、今回の例では以下のような回帰直線が出てきます。

y(x) = 72.42553526668996 + 1.847068 x

$x=35.6$を代入して$y$を求めてみましょう。

y(35.6) = 138.181156067

すると、はじめに直観的に得た140cmに近い数値がでてきました。

次に、この回帰直線を得る方法、具体的には係数$w_0, w_1$を求める方法について考えます。

実は、この方法は皆さんご存知の回帰係数を求める方法そのものです。$x$の係数である$w_1$が回帰係数となります。

回帰係数を求める方法を思い出しましょう。

まず入力データを以下のようにベクトルとして捉えます。

\vec{x} = ( x_0\, x_1\, x_2\, \dots\, x_N )^T.

今回の例では、この$\vec{x}$には15人それぞれの体重が要素として入ります。従って$N = 15$です。

次に目的となるデータ(今回の場合は身長)をベクトルとして捉えます。

\vec{t} = ( t_0\, t_1\, t_2\, \dots\, t_N )^T.

ここで誤差関数$E(w_0, w_1)$を定義します。

E(w_0, w_1) = \frac12 \sum_{i=0}^{N} (y(w_0, w_1, x_i) - t_i)^2.

この$E(w_0, w_1)$を最小にするような$w_0, w_1$を求めることが、回帰係数を求めるときにやったことでした。そして、ここでも同じことをやります。

それにはいつも使われるテクニックがありました。それは

\left(
\begin{matrix}
\frac{\partial E}{\partial w_0} \\
\frac{\partial E}{\partial w_1}
\end{matrix}
\right)
=
\left(
\begin{matrix}
0 \\
0
\end{matrix}
\right)

を成立するような$w_0, w_1$を求めることでした。

ここまでくれば、あとは行列の計算をすればいいだけです。

すると以下のような行列の式がでてくるでしょう：

X^T X \vec{w} - X^T \vec{t} = \vec{0}, 

ただし、$X$と$\vec{w}$はそれぞれ

X = 
\left(
\begin{matrix}
1 & 1 & \cdots & 1 \\
x_0 & x_1 & \cdots & x_N 
\end{matrix}
\right)^T, 

\vec{w} =
\left(
\begin{matrix}
w_0 \\
w_1 
\end{matrix}
\right)

とします。

この式の導出はこのページの最後にしてます。

この式を変形すると以下のようになります：

\begin{align}
X^T X \vec{w} - X^T \vec{t} &= \vec{0} \\
X^T X \vec{w} &= X^T \vec{t} \\
\vec{w} &= (X^T X )^{-1} X^T \vec{t}
\end{align}.

確認

• 1. (sklearnを使わずに)回帰直線を求める機能を実装したあと、上の例で挙げた15人のデータセットから回帰直線を描写してください。
  • 実はsklearnというライブラリを使えば、自分で実装することなく回帰を行えます。今回は理解を重視するためにこのライブラリを使わずに実装してみてください。
• 1. 16人目の体重が40.7kgとして、予測される身長を出力してください。

多項式回帰を理解して実装する

説明

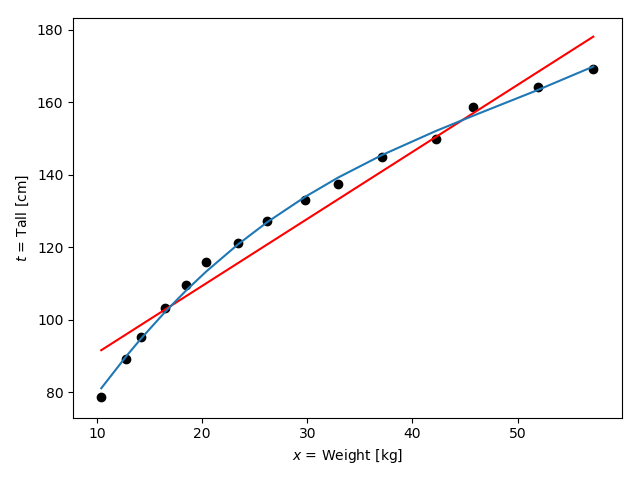
ところで、上の例は直線で回帰しましたが、気分としては、以下のような青い曲線で回帰したくならないでしょうか。

そういうときは、実は目的関数$y$を多項式にするだけでよいです。

\begin{array}

 \, y(\vec{w}, x) &= \sum_{i=0}^{M} w_i x^i \\
              &= w_0 + w_1 x + w_2 x^2 + w_3 x^3 + \cdots w_M x^M,
\end{array} 

ただし、$\vec{w}=(w_0 , w_1 , w_2 , \cdots , w_M)^T$とします。

ここでテイラー展開を思い出してみてください。テイラー展開によって、ただ多項関数にするだけでも様々な関数を表現できることがわかります。

さて、実際にこの多項関数に回帰させるにはどうすればよいか、-- それも線形回帰と何ら変わりません。同じ方針で計算してみてください。

行列の計算で迷われた方は正規方程式の導出と計算例をご参照ください。

すると以下のような連立方程式ができます。線形回帰と形式的には同じものになっていますね。

X^T X \vec{w} - X^T \vec{t} = \vec{0}, 

ただし、$X$と$\vec{w}$はそれぞれ

X = 
\left(
\begin{matrix}
1 & 1 & \cdots & 1 \\
x_0 & x_1 & \cdots & x_N \\
x_{0}^2 & x_{1}^2 & \cdots & x_{N}^2 \\
\vdots & &  & \vdots \\
x_{0}^M & x_{1}^M & \cdots & x_{N}^M
\end{matrix}
\right)^T, 

\vec{w} =
\left(
\begin{matrix}
w_0 \\
w_1 \\
\vdots \\
w_M
\end{matrix}
\right)

とします。

この式の導出も最後にします。

この節であげた例は$M=3$としたときの曲線です。出力された目的関数は以下のようになりました。

y(x) =   32.28082825688925 + 5.58539641 x -  0.0918462798 x^2 + 0.000633627190 x^3.

$x=35.6$を代入すると

y(35.6) = 143.302

となり、直線で回帰したときよりもよりそれらしい数値がでてきました。(なぜそれらしいと表現したくなったかを説明します: 体重が体積に比例し、かつ16人目の子が標準的な体重の持ち主であると仮定しましょう。ここで体積は、単位㎤などで示唆されるように、長さの三乗に比例します。したがって体重の増加量$n$に対して身長の増加量は$\sqrt[3]{n}$となると考えれば、少なくとも二つの値の平均よりも大きな値が出た方がそれらしい、ですよね？)

実践問題

• ★1. (sklearnを使わずに)多項式回帰を実装してください。
• ★2. Cycle1の実践問題で作成したテストデータを多項式回帰で曲線をだしてください。うまく三角関数が再現できたら成功です。
• 1. 以下の参考からsklearnを使って線型回帰、多項式回帰をしてみてください。結果は変わりますか？
• 1. 多項式回帰で、次数の数$M$をどんどん大きくしてゆくとどんな現象が生じますか？ => 過学習

#参考

• scikit-learn document: http://scikit-learn.org/stable/user_guide.html
  • ridge regression: http://scikit-learn.org/stable/modules/kernel_ridge.html
  • LinearRegression: http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html
  • LinearRegression Example: http://scikit-learn.org/stable/auto_examples/linear_model/plot_ols.html#sphx-glr-auto-examples-linear-model-plot-ols-py
  • PolynomialRegression: http://scikit-learn.org/stable/modules/linear_model.html#polynomial-regression-extending-linear-models-with-basis-functions
• python+scikit-learnで多項式曲線近似をリッジ回帰で求める
• scikit-learn Ridge: http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.Ridge.html
  • 例

補足

扱おうと思ったけどやめたこと

• 重回帰
• 罰金項の追加による過学習の抑制(Ridge回帰)
• 勾配降下法
• 実データを使った分析

正規方程式の導出

$M$次の多項式の場合。線形の正規方程式は$M=1$とすればよい。

\begin{align}
E(\vec{w}) &= \frac12 \sum_{i=0}^{N} (y(\vec{w}, x_i) - t_i)^2 \\
&= \frac12 || X \vec{w} - \vec{t} ||^2 \\
&= \frac12 (|| X \vec{w} ||^2 + || \vec{t} ||^2 - 2 X \vec{w} \cdot \vec{t}).
\end{align}

ここで以下の表記を導入する：

\frac{\partial f(\vec{w})}{\partial \vec{w}} := 
\left(
\begin{matrix}
\frac{\partial f(\vec{w})}{\partial w_0} \\
\frac{\partial f(\vec{w})}{\partial w_1} \\
\vdots \\
\frac{\partial f(\vec{w})}{\partial w_M} \\
\end{matrix}
\right) ,

ただし、$\mathbb{R}^M \ni \vec{w} \longmapsto f(\vec{w}) \in \mathbb{R}$.

つまり求める式は以下：

\frac{\partial E(\vec{w})}{\partial \vec{w}} = \vec{0}.

ここで以下の二つを気にする。

\begin{align}
\frac{\partial}{\partial \vec{w}} || X \vec{w} ||^2 &= 
2 \left(
\begin{matrix}
\sum_{k=0}^{N} x_k^0(\sum_{i=0}^{M} w_i x_k^i ) \\
\sum_{k=0}^{N} x_k^1(\sum_{i=0}^{M} w_i x_k^i ) \\
\vdots \\
\sum_{k=0}^{N} x_k^M(\sum_{i=0}^{M} w_i x_k^i ) 
\end{matrix}
\right) \\
&=2  X^T X \vec{w},
\end{align}

\begin{align}
\frac{\partial}{\partial \vec{w}} X \vec{w} \cdot \vec{t} &= 
\left(
\begin{matrix}
\sum_{k=0}^{N} x_k^0 t_k \\
\sum_{k=0}^{N} x_k^1 t_k \\
\vdots \\
\sum_{k=0}^{N} x_k^M t_k
\end{matrix}
\right) \\
&= X^T \vec{t} .
\end{align}

従って、

\begin{align}
\frac{\partial E(\vec{w})}{\partial \vec{w}} &=  X^T X \vec{w} - X^T \vec{t}.
\end{align}

Ridge回帰の正規方程式導出

R(\vec{w}) := \frac12 || X \vec{w} - \vec{t} ||^2 + \frac{\lambda}{2} || \vec{w}||^2, \ \lambda > 0. \ 

\frac{\partial}{\partial \vec{w}} || \vec{w} || ^2 = 2 \vec{w} \ 

なので

\frac{\partial}{\partial \vec{w}} R(\vec{w}) = \vec{0},

\therefore \ 
(X^T X + \lambda E) \vec{w} - X^T \vec{t} = \vec{0}.