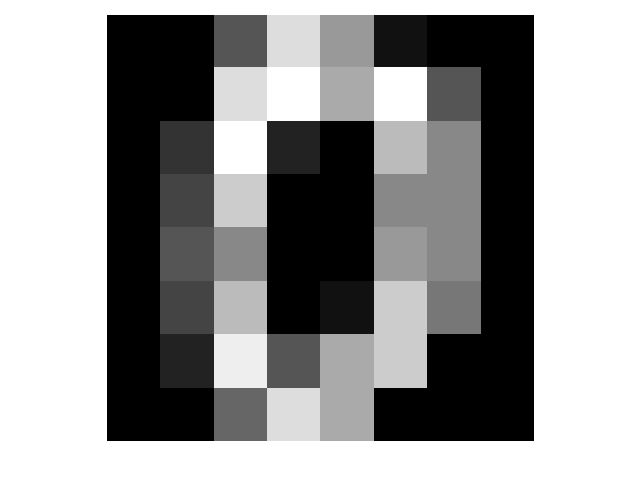Go to Qiita Advent Calendar 2024 Top
LoginSignup
0
3

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 5 years have passed since last update.

@kenji-kondo(近藤 憲児)

PythonでやるML Cycle4: k-means法でAIを作る

Last updated at Posted at 2018-12-18

教師なし学習 について

ゴール

  • 教師なし学習の概要を知る
  • scikit-learnのデータセット(画像)を扱ってみる
  • scikit-learnのKMeansを使って画像を分類する
  • k-meansのアルゴリズムを理解して自分で実装する

モチベーション

教師なしで学習するとはどういうことか

このCycle4は、前回までやったCycle2やCycle3とちょっと毛色が異なります。

前回まで扱ったデータには正解がありました。Cycle2では、体重から身長の予測をするために、15人分の体重と、正解データである身長のデータを予め知っていて、それらを学習させて予測しようとしました。Cycle3では、葉の長さと幅の組み合わせから職人さんのOK/NGの判断を予測するために、20個分の葉の長さ、幅の組み合わせと、正解データであるOK/NGの対応を予め知っていて、同様にこれらで学習させて予測を行いました。こうした正解データを使った学習を教師あり学習と呼びます。

今回は、手書きで記された数字の画像をプログラムに何の数字かを識別させる、ということをやります。今までの考え方の延長で考えれば、手書きで記された画像(個々のピクセルに対して定まったRGB値の集まり、など)に対し、正解である数字(0や8などの文字列、など)の組み合わせデータが必要となることでしょう。

しかし、今回はあえて正解データを使いません。手書きで記された数字の画像だけを用いて、プログラムに識別させます。これがいわゆる教師なし学習です。

プログラムが他人に教えられることなく自分で学んで区別するなんて、まさに素朴に想像する「AI」ではないでしょうか。誇張が過ぎる表現なのも理解しますが、純粋に面白く感じます。

では、一体どのようにしてそのようなことを実現できるのか、その一例をご紹介します。

転校生の例

皆さんは転校を経験したことがあるでしょうか。私はありません。なので今から書くことは想像です。

転校初日、黒板の前に立たされ見渡す視野にいる人間をみな、同質なものに思うことでしょう。都会にあるこの学校の人は"全員"、放課後にスタバに寄っておしゃれにフラペチーノ飲んでるのだろう、と。私のようにその辺に生えてる木からはっさくをむしり取ってしゃぶりながら帰るなんてことしないだろう、と。

しかし、一週間ほどクラスの中を観察すると、クラスの中を小さなグループに分けられることに気づきます。放課後にフラペチーノを飲んでいる人たちもいれば、ひたすらお絵かきして過ごしている人たち、ほうきでいつも野球をしている人たち、そして自分の気の合う仲間たち、という具合に。クラスで話したことのない人がいても、その人を見ているだけで、誰々がいるグループの人だ、ということがなんとなくわかります。

さて、この事象を振り返ると、私たちがグループを識別できるようになることに、誰にも教えてもらうことなく到達できました。これは日常生活における教師なし学習と言えるでしょう。

では、グループを識別できるようになるために、私たちは何を見ているのでしょう。

色々なことが考えられますが、ここでは一つ大きなファクターとして「人と人の間の(物理的な)距離」を挙げます。

放課後フラペチーノグループは、昼休みも互いに(物理的に)近い距離で集まって会話を楽しんでいます。ひたすらお絵かきグループは(物理的に)近い距離で集まってお絵かきしています。私たちは(物理的に)近い距離で連れ立ってトイレに行きます。

このような**「人と人とが互いが物理的に近い距離にいる集団は、同じグループである」**という仮説は、科学的事実かどうかはさておき、どうでしょう、感覚的に尤もらしく感じないでしょうか。思えば、動物の中には群れをなすものも存在することを、幼少の頃から知っています。サバンナの航空写真を見せられて、そこにガゼルの群れが二つある、ということを無意識に判断してしまうほどには、私たちの中に刷り込まれている感覚です。

この考え方を、正解データなしの画像分類に応用します。

画像と画像の"距離"？

上に述べた考え方を画像に対して適用すると、**「画像と画像とが互いに近い距離にあるものたちは、同じグループである」**ということになります。

言わずもがな、画像と画像の距離とはなんだ、と思うでしょう。それは次のように考えてみましょう。

簡単にグレースケールの画像で考えます。以下は、色の指定が0～16の諧調で指定された、8×8ピクセルの画像です。

image.png

大分荒い画像ですが、これは数字の「0」です。

次に、この画像の濃淡を0～16で置き換えたものが以下です。黒さが増すほど値は0に近づきます。

[[ 0.  0.  5. 13.  9.  1.  0.  0.]
 [ 0.  0. 13. 15. 10. 15.  5.  0.]
 [ 0.  3. 15.  2.  0. 11.  8.  0.]
 [ 0.  4. 12.  0.  0.  8.  8.  0.]
 [ 0.  5.  8.  0.  0.  9.  8.  0.]
 [ 0.  4. 11.  0.  1. 12.  7.  0.]
 [ 0.  2. 14.  5. 10. 12.  0.  0.]
 [ 0.  0.  6. 13. 10.  0.  0.  0.]]

なんとなく0に見えなくもないですね。

では、唐突ですが、この数字を横一列に並び替えます。アルファベットのZをなぞるように上の列を並び替えると、以下のようになりました。

[ 0.  0.  5. 13.  9.  1.  0.  0.  0.  0. 13. 15. 10. 15.  5.  0.  0.  3.
 15.  2.  0. 11.  8.  0.  0.  4. 12.  0.  0.  8.  8.  0.  0.  5.  8.  0.
  0.  9.  8.  0.  0.  4. 11.  0.  1. 12.  7.  0.  0.  2. 14.  5. 10. 12.
  0.  0.  0.  0.  6. 13. 10.  0.  0.  0.]

最後に、この横一列で並んだものを8×8(=64)次元のベクトルと見なします。

\vec{x_0} = ( 0  \, , 0  \, , 5  \, , 13  \, , 9  \, , 1  \, , 0  \, , 0  \, , 0  \, , 0  \, , 13  \, , 15  \, , 10  \, , 15  \, , 5  \, , 0  \, , 0  \, , 3  \, , 15  \, , 2  \, , 0  \, , 11  \, , 8  \, , 0  \, , 0  \, , 4  \, , 12  \, , 0  \, , 0  \, , 8  \, , 8  \, , 0  \, , 0  \, , 5  \, , 8  \, , 0  \, , 0  \, , 9  \, , 8  \, , 0  \, , 0  \, , 4  \, , 11  \, , 0  \, , 1  \, , 12  \, , 7  \, , 0  \, , 0  \, , 2  \, , 14  \, , 5  \, , 10  \, , 12  \, , 0  \, , 0  \, , 0  \, , 0  \, , 6  \, , 13  \, , 10  \, , 0  \, , 0  \, , 0)^T

こうして、最初の画像をベクトル$\vec{x_0}$として表現しなおしました。

同じ調子で、すべての画像をベクトル$\vec{x_1}, , \vec{x_2}, , \dots$として表現しなおしましょう。すると「画像と画像とが互いに近い距離にあるものたちは、同じグループである」は、以下のように言い換えられるでしょう：

「ベクトルとベクトルとが互いに近い距離にあるものたちは、同じグループである」

ではベクトルの距離とは何でしょうか？ --- はじめに思い浮かぶものはユークリッド距離でしょう。ユークリッド距離とは、以下のようにノルムで定義された距離で、2次元や3次元の場合は平面(あるいは空間)上の"長さ"に相当します。

|| \vec{x_i} - \vec{x_j} || = \sqrt{ \sum_k (x_{ik} - x_{jk})^2}.

こうして、「画像と画像の距離」というものを、私たちが扱える形(つまりベクトルとして表現することで線形代数の知見を使える形)にすることが考えることができるようになりました。

ちなみに、距離を考えることはすなわちユークリッド距離を考えることである、ということではありません。距離には様々な種類があります。ユークリッド距離以外で有名なものと言えばマンハッタン距離でしょうか。点から点に移動するときに碁盤目状にしか動けないとして、その最短経路の長さを距離と定義したものです。また統計学の中で出てくるものにマハラノビス距離というものもあります。下部の参考にあげているスライドがわかりやすいです。

距離というのは、実は数学的な定義が存在します。すなわち、この距離の定義を満たしているものは一つ残らず(数学的に)距離と呼ぶことができます。言い換えれば、自分で定義したもの(関数)が距離の定義を満たしているならば、たとえそれがどれだけ奇怪なものであっても、数学的に正しい距離となります。例えば、ある条件を満たす関数$f(x)$と$g(x)$の距離を、以下のように定義できます：

|| f - g || = \sqrt{ \int_{\Omega} |f(x) - g(x)|^2 dx}.

これが距離の定義を満たしていることは証明できます。こうした関数の間の距離を考えることが、桶屋が儲かる的な長い因果の鎖を辿ると、天気予報が100%当たるようにするための研究を支えていたりします。

モチベーション

前置きが長くなりましたが、これからやりたいのは

「ベクトルとベクトルとが互いに近い距離にあるものたちは、同じグループである」

という判断を、プログラムにさせることです。

そして、それを行うための具体的なアルゴリズムとして**k-means(法)**があります。今からこのk-meansについて、詳しく説明していきます。

手書き数字データの準備

digits-dataset

k-meansの説明に入る前に、手書きデータの準備を行います。

手書きデータはscikit-learnにもともと入っているdigits-datasetを使います。これはテスト用のデータセットで、sklearnのライブラリさえ使える状態ならばダウンロードなどの必要なく利用できます。scikit-learnはこの他にもいくつかのテスト用のデータセットを持っています。

以下で手書きデータを取り込むことができます。

from sklearn.datasets import load_digits
digits = load_digits()

上のdigitsの使用方法を例示します。

  • 画像を描写する
import matplotlib.pyplot as plt
plt.imshow(digits.images[0])
plt.axis('off')
plt.gray()
plt.show()

OUTPUT

image.png

  • この画像のトレーニングデータ(numpy.ndarray型になっている)
print(digits.data[0])

OUTPUT

[ 0.  0.  5. 13.  9.  1.  0.  0.  0.  0. 13. 15. 10. 15.  5.  0.  0.  3.
 15.  2.  0. 11.  8.  0.  0.  4. 12.  0.  0.  8.  8.  0.  0.  5.  8.  0.
  0.  9.  8.  0.  0.  4. 11.  0.  1. 12.  7.  0.  0.  2. 14.  5. 10. 12.
  0.  0.  0.  0.  6. 13. 10.  0.  0.  0.]
  • この画像の正解
print(digits.target[0])

OUTPUT

0

確認

  • 以下のAPIリファレンスをざっと読んで、概要や使い方を掴んでください。
  • 取り込んだデータを使って以下を確かめてください。
    • なんでもいいので画像を描写してください。どんな画像がありますか？
    • 手書きデータは全部で何個ありますか？
    • 手書きデータの中で「0」と「1」だけを扱いたい場合、どのような方法がありますか？
    • 以下のように、画像を並べて表示できるようになってください。結果を確かめるときに画像を並べてみたくなると思いますので。私はGridSpecを使ってやりました。

image.png

k-meansをscikit-learnで実装する

KMeans

まず、k-meansの"k"は、分類するグループ(クラスタと呼ぶ)の個数を意味します。この個数kは実装者があらかじめ設定しておく必要があります。例えば「0」と「1」の画像群を識別させる場合、k=2となります。識別するクラスタの個数自体は、k-meansでは自動的に出力してくれませんのでご注意ください。

ひとまず、手っ取り早くライブラリを使ってk-meansをやってみます。使うライブラリはsklearn.cluster.KMeansです。

APIリファレンス: https://scikit-learn.org/stable/modules/generated/sklearn.cluster.KMeans.html

このAPIリファレンスにあるExamplesが、下手に説明するよりもわかりやすいです。実際に動かしてみてください。

確認

  • digitsに対してk-meansで分類してみてください。

k-meansを自分で実装する

k-meansのアルゴリズム

ここからはk-meansのアルゴリズムについて説明します。これははじめてのパターン認識の説明に準拠しています。

まず$K$を分類するクラスタの個数とします。例えばデータセット全体を2つに分類する場合は、$K=2$となります。

次にクラスタを集合で定義します。

まずデータを$\vec{x}_i$というベクトルで表現します。これまでに述べた例に沿えば、このベクトル一つが画像一枚に相当します。データが複数あるので、その$i$番目のデータであるとわかるように、下付きの添え字で表します。

データセットの数を$N$として、データセット全体の集合$\mathcal{D}$を$\mathcal{D} = \{ \vec{x_1}, , \vec{x_2}, , \dots , , \vec{x_N} \}$と定義します。そして$K$個クラスタ$\mathcal{M}_1, , \mathcal{M}_2, , \dots , , \mathcal{M}_K$を、以下を満たす$\mathcal{D}$の部分集合として定義します：

\bigsqcup_{k=1}^{K} \mathcal{M}_k (= \mathcal{M}_1 \sqcup \mathcal{M}_2 \sqcup \cdots \sqcup \mathcal{M}_K) = \mathcal{D},

ここで$\mathcal{A} \sqcup \mathcal{B}$は、$\mathcal{A} \cup \mathcal{B}$かつ$\mathcal{A} \cap \mathcal{B} \neq \emptyset$という意味です。つまりクラスタは、データセットを重複なく、完全に分割したものとして定義されます。

また「ベクトル$\vec{x_n}$が、クラスタ $\mathcal{M}_k$に属している」ことを表現するために、以下の関数$q$を定義します。

q_{nk} = \left\{
\begin{array}{ll}
1 & (\vec{x_n} \in \mathcal{M}_k) \\
0 & (\vec{x_n} \notin \mathcal{M}_k)
\end{array}
\right.

この$q_{nk}$の役目は、$\vec{x_n}$が集合$\mathcal{M}_k$に含まれるか否かを示す、いわゆるフラグです。この表現を使えば以下が成立します：

|\mathcal{M}_k| = \sum_{n=1}^N q_{nk},

ここで$|\mathcal{M}_k|$は、集合$\mathcal{M}_k$に含まれるベクトルの個数を意味します。

さらに、クラスタ$\mathcal{M}_k$に所属するベクトル$\vec{x}$の平均ベクトル(セントロイドと呼ぶ)を$\vec{\mu_k}$で表します。これは、上で導入した関数$q$を使えば以下のように表現できるでしょう：

\vec{\mu_k} = \frac{\sum_{n=1}^N q_{nk} \vec{x_n}}{\sum_{n=1}^N q_{nk}}.

ここまでが記号の導入です。

ここまでに導入した記号を使って今からやることの目的を述べると、「データセットを使って、最適な$\{ q_{nk} \}$と$\{ \vec{\mu_k} \}$たちを求めること」となります。ここでいう"最適"とは、以下の評価関数$E(q_{nk}, \vec{\mu_k})$を最小にする$q_{nk}$, $\vec{\mu_k}$を求めることに相当します：

E(q_{nk}, \vec{\mu_k}) = \sum_{k=1}^K \sum_{n=1}^N q_{nk} || \vec{x_n} - \vec{\mu_k} ||^2

まず$q_{nk}$を固定して考えたときは、いつも通り$\frac{\partial E}{\partial \vec{\mu_k}} = \vec{0}$となる$\vec{\mu_k}$を求めればいいです。計算してみると、

\vec{\mu_k} = \frac{\sum_{n=1}^N q_{nk} \vec{x_n}}{\sum_{n=1}^N q_{nk}}

を計算すればよいことがわかります(下の補足に具体的な計算過程を載せています)。

一方、$q_{nk}$のほうの最適化はこのようにきれいにいきません。なので、以下のように逐次的に$q_{nk}$を最適化してゆく方式をとります。

上記をもろもろまとめると、以下のステップで最適化すればいいです：

  1. 初期値として、データセット$\{ \vec{x_n} \}$を$K$個のクラスタにランダムに振り分ける(つまり$\{ q_{nk} \}$をランダムに定める)。
  2. ($\vec{\mu_k}$の最適化) セントロイド$\vec{\mu_k}$を求める。
  3. ($q_{nk}$の最適化) データ $\vec{x_n}$ とセントロイド$\mu_1, , \mu_2, , \dots, , \mu_K $ との距離をそれぞれ計算して、
    その中から最も距離が短いものに対応する $k$ を選ぶ。そしてその $k$ に対し、$\vec{x_n} \in \mathcal{M}_k$とする。
  4. 上の2.と3.を繰り返す。いずれ何も更新されなくなるので、その状態になるまでやる。

以上、k-meansのアルゴリズムの説明でした。

実践問題

  • ★1. 上の方式に従ってk-meansを実装してください。
  • ★2. digitsの「0」と「1」の手書きデータを使って分類してみてください。
    1. セントロイド$\vec{\mu_k}$を画像として描写してください。平均的な「0」と「1」が描写されるでしょう。(もしも日本人の顔写真に対してこれを行ったら、平均的な日本人顔が描写できるでしょう。面白そうなのでやってみたいですね。)
    1. 新しい数字の手書きデータがどのクラスタに入るのかを判別するmethodpredictを実装するとしたら、どのようなロジックになりますか？

補足

k-means++

sklearnのKMeansでは実際にはk-means++というアルゴリズムが使われている。

k-means++: http://ilpubs.stanford.edu:8090/778/1/2006-13.pdf

k-meansとの違いは、初期値としてのセントロイドの取り方にある。初期値としてランダムにセントロイドを選択すると、運が悪ければセントロイド同士が近くなっちゃう。それを回避するために、一つセントロイドを決めたら、次のセントロイドは遠いものを選ぶ、というのを繰り返すことで、初期値のセントロイドが互いに遠く存在できるようにする。

具体的な操作は以下。上の論文のコピー

image.png

$\mathcal{X}$はデータセット全体の集合。

これを実装してみたけれど、正直今回のデータセットではあんまり優位性がわからなかった。いずれであれ、「1」と「2」の区別がわかりづらいようだ。

scikit-learnのKMeansのサンプルコード

「0」と「1」を見分けて、それを表っぽく描写する。

import matplotlib.gridspec as gridspec
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import load_digits

# 何個の数字を見分けたいか
n = 2
digits = load_digits(n_class=n)

# KMeans実行
km = KMeans(n_clusters=n).fit(digits.data)

# 描写
# (n)行(num_columns)列の画像の表を作る
num_columns = 10
gs = gridspec.GridSpec(km.n_clusters, num_columns)
plt.gray()
x = {}
for t in range(km.n_clusters):
    x[t] = 0
for i in range(len(km.labels_)):
    plt.subplot(gs[km.labels_[i], x[km.labels_[i]]])
    plt.imshow(digits.images[i])
    plt.axis('off')
    x[km.labels_[i]] += 1
    if x[km.labels_[i]] >= num_columns:
        break
plt.show()

出力

image.png

μの最適化の具体的な計算

まず$q_{nk}$を固定して考えたときは、いつも通り$\frac{\partial E}{\partial \vec{\mu_k}} = \vec{0}$となる$\vec{\mu_k}$を求めればいいです。

の部分の計算。

まず準備として、以下を示しておく。

\frac{\partial}{\partial \vec{x}} || \vec{a} - \vec{x} ||^2 = -2 ( \vec{a} - \vec{x}),

ただし、$\vec{a} = ( a_1, a_2, \dots, a_N)^T$, $\vec{x} = ( x_1, x_2, \dots, x_N)^T$.

証明

\begin{align}
\frac{\partial}{\partial \vec{x}} || \vec{a} - \vec{x} ||^2 &= \frac{\partial}{\partial \vec{x}} \sum_{n=1}^{N} (a_n - x_n)^2 \\
&= 
\left(
\begin{matrix}
-2 (a_1 - x_1) \\
-2 (a_2 - x_2) \\
\vdots \\
-2 (a_N - x_N)
\end{matrix}
\right) \\
&= -2 (\vec{a} - \vec{x}).
\end{align}

証明終わり

まず$\frac{\partial E}{\partial \vec{\mu_{k_0}}}$を計算する。

有限和であるので、偏微分の計算順序を変更できる。

\begin{align}
\frac{\partial E}{\partial \vec{\mu_{k_0}}} &= \frac{\partial}{\partial \vec{\mu_{k_0}}} \sum_{k=1}^K \sum_{n=1}^N q_{nk} ||\vec{x_n} - \vec{\mu_k}||^2 \\
&=  \sum_{n=1}^N \frac{\partial}{\partial \vec{\mu_{k_0}}} \sum_{k=1}^K q_{nk} ||\vec{x_n} - \vec{\mu_k}||^2 \\
&= \sum_{n=1}^N \frac{\partial}{\partial \vec{\mu_{k_0}}} q_{n k_0} ||\vec{x_n} - \vec{\mu_{k_0}}||^2 \\
&= \sum_{n=1}^N q_{n k_0} \cdot (-2 (\vec{x_n} - \vec{\mu_{k_0}})) \\
&= -2 \left(\sum_{n=1}^N q_{n k_0} \vec{x_n} - (\sum_{n=1}^N q_{n k_0}) \vec{\mu_{k_0}} \right), 
\end{align}

ここで、$\frac{\partial}{\partial \vec{\mu_{k_0}}} ||\vec{x_n} - \vec{\mu_k}||^2$は$k=k_0$でなければすべて0であることに注意する。

今出した式$=\vec{0}$となる方程式を解けばでてくる。

参考

0
3
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
3

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?