Go to Qiita Advent Calendar 2024 Top
LoginSignup
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 5 years have passed since last update.

@kenji-kondo(近藤 憲児)

PythonでやるML Cycle3: 線形識別関数で自動分類機を作る

Last updated at Posted at 2018-11-28

教師あり分類について。

ゴール

  • 線形識別の概要を知る。
  • scikit-learnで線形識別を体験する。
  • 線形識別を数学的に理解して、その理解をもとに自分で線形識別を実装する。

モチベーション

伝統工芸職人VS新人

以下のようなシチュエーションで考えます：

とある町に、木材を使った伝統工芸品を作る職人さんがいました。その職人さんが作るものは物持ちが良いことで有名で、その人が所属する会社はその職人さんの腕に頼り切りでした。

その職人さんの特徴として、材料となる木材を取り寄せたときには必ず、その木材にもともとついていた葉を同時に要求することにあります。その職人さんはその葉をじっと眺めると、「これはだめだ」「これは良い」と判断します。そして、その職人さんが良いと判断したものは、確かに物持ちが良い傾向にあることがわかっています。

葉のつき方とその木材の品質の良さになんらかの関係があることまでは推測できますが、科学的にはわかっていません。これは非科学的な何かに起因しているという意味ではなく、科学的な調査をすればいずれわかることなのかもしれませんが、それをして因果関係を発見できる目途と調査費用の折り合いがつかず、調査自体を行えない状態にあるからです。つまりその職人さん以外の人は、「理由はわからないけど、葉の何かを見れば、その木材の品質の良さを判断できる」という程度の理解しかありません。

さて、この職人さんが突然引退を宣言しました。その会社の人は困りました。この職人さんの技術がなければ会社が終わる。科学調査を始めるにも、引退までの時間はあまり残されていません。最近は職人の技術に目を輝かせる"ワカモノ"が入ってこないし、この前入ってきた生意気な新人は、クラウドだのAIだの、よくわからない言葉を放つばかり。この職人さんと新人は相性が良いとは決して言えず、技術の伝承もうまくいっていない。会社に暗雲が立ち込めました。

そんなとき、そのクラウドだのAIだの放っていた生意気な新人が放ちます：「俺、秘密わかりましたよ」

その新人に注目が集まります。「ほう、それはどういうことだ」引退を宣言した職人さんも、この言葉には興味を示します。

果たして、その新人が発見した秘密とは？IT新人と伝統技術職人の二人の物語が今、云々。

書いててちょっと楽しくなってきました。後半のセリフ部分はどうでもいいです。

新人の発見した秘密

この新人が発見した秘密とやらは、葉の長さに注目したところにありました。

以下のデータにその新人が調査したデータがあります。

leaves.csv
length,width,label
10.616973750579737,7.1620634157936225,1
10.603006432465996,6.875613098344005,1
10.86679532399243,7.008832193534252,1
10.05649100712974,7.574822390843004,1
10.17678399477045,7.487858550188874,1
10.267879298974645,7.120404761968314,1
10.436763038314353,7.724122427899155,1
10.460606791277353,7.796560118741979,1
10.158287903626587,6.987802904094496,1
9.967458440114711,7.06316783713265,1
11.201002656520972,4.4191880142082,-1
11.408407706848331,5.061532847373223,-1
11.013823592600694,5.23637797087632,-1
11.907807724826595,4.902961019272424,-1
11.839985328062925,5.085639591353499,-1
11.490365258916706,4.94989938227516,-1
10.99034177757561,4.572030881622861,-1
10.797466999283568,4.920484891075101,-1
11.450903645052671,4.635310547847377,-1
11.456089593970573,5.258671641403568,-1

Lengthは葉一の真ん中を走る1番太い葉脈に平行に測ったときの最大値、Widthは同じく葉一枚を葉脈に垂直に測ったときの最大値、Labelは例の職人さんによる良い(=1)、悪い(=-1)を判断を示しています。

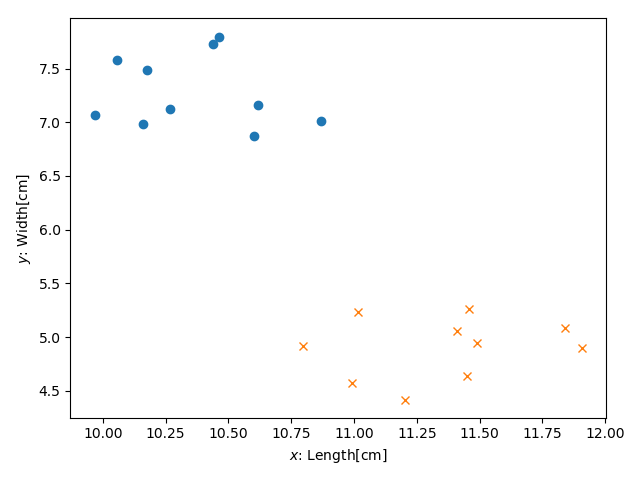
このままではわかりにくいので、二次元の$x,y$平面にプロットしてみます。

image.png

ここまで見せられると、大した秘密に思えなくなりますね。例えば葉一枚のLength,Widthがそれぞれ11.0, 5.2である木材を、例の職人さんは良い悪いどちらと判断すると予想できるでしょうか。

この点をプロットしてみると、多くの人は以下のように推測するでしょう:「プロットした点のそばにバツが沢山あるから、多分これはダメだろう」

これが新人が発見した秘密です。

ちなみに、ひょっとすると上のプロットしたデータを見て「なんだ、こんなもの誰だってわかる」と言いたくなるかもしれません。このシチュエーションは創作なのでその通りですが、実際の現場でこのように簡潔な結果を提示してきた人がいたならば、それはきっと誉めるべきです。その人は葉の長さ以外にも、葉の形状、葉脈の本数など、様々なパラメータ同士の関係を調査して、その結果、OK/NGに大きく影響するパラメータがこの2つしかないことを導き出したのでしょう。このように、大量のパラメータの中から結果に大きな影響を及ぼす少数の成分を抜き出して、データの見方をわかりやすくする手法の代表的なものに主成分分析があります。これはこれで面白い話題なので次のCycleで扱おうと思います。ともあれ、簡潔な結果を導くことにも技術を伴う、ということを強調しておきます。

モチベーション

今からやりたいのは、

「プロットした点のそばにバツが沢山あるから、多分これはダメだろう」

という、人間にはおなじみの思考を、機械にやらせることです。どのようなアルゴリズムでこれを実現できるのか、考えていきます。

scikit-learnを使った実装

説明

自分で実装する前に、sklearnを使って手っ取り早く結果のイメージをつかみたいと思います。

sklearnのPerceptronクラスを使って線形識別を行います。

以下では上述したCSVをcycle3/resources/leaves.csvに配置しています。環境に合わせて適宜変更してください。

from sklearn.linear_model import Perceptron
import pandas as pd

data = pd.read_csv('cycle3/resources/leaves.csv')

ppn = Perceptron(max_iter=20, eta0=0.1, random_state=1)
ppn.fit(data[['length', 'width']], data['label'])
predicted_label = ppn.predict([[11.0, 5.2]])
print(predicted_label)

ppn = Perceptron(max_iter=20, eta0=0.1, random_state=1)で、学習に必要なパラメータをセットしています。3つパラメータが出てきますが、これは後に理解できると思います。

ppn.fit(data[['length', 'width']], data['label'])で学習し、その学習したものをもとにppn.predict([[11.0, 5.2]])で予測しています。

確認

  • 上記のコードを実行してください。結果が以下のようになれば成功です。
[-1]

線形識別のアルゴリズムを理解して実装する

アルゴリズムのアイディア

ここからは、具体的なアルゴリズムについて解説します。一つ注意として、以下に説明するところはsklearnの内部の実装ではありません。PerceptronのAPIリファレンスを見ると、fitの中では確率的勾配降下法が用いられていますが、今から説明するのはちょっと違います。ここでは、精度や学習速度はつたないものの最も単純でわかりやすいアルゴリズムで紹介します。しかしながらコアな部分は変わらないので、これを理解すれば新しいアルゴリズムであっても理解しやすいと思います。

さて、本題です。

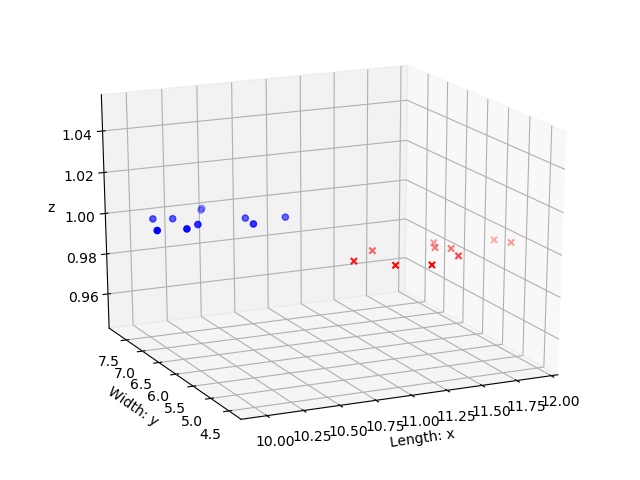
いきなりトリッキーな発想ですが、この2次元のデータを3次元で捉えなおします。例えば

(x,y) =(10.616973750579737,7.1620634157936225)

というデータを、$z=1$を付与して以下のように3次元で捉えなおします。

(x, y, z)=(10.616973750579737,7.1620634157936225, 1).

上のように3次元目の$z$を増やし、かつ$z=1$とすれば、$z=1$の平面上にすべての点が載っています。宙に浮いた○と×の集まりがイメージできればOKです。

image.png

ここから先は頭の中でイメージしてください。ここでそれら二つの集団を分断するように、原点を通る平面を書きます。平面によって分断された空間の片側に○が集まっていて、かつもう片側に×が集まっているイメージができればOKです。

この平面によって、以下のような判断ができるようになりました：「平面の上側にあれば○、平面の下側にあれば×」

しかしまだあやふやです。「平面の上側」の定義はなんでしょう。例えば平面が$x-y$平面に垂直である場合、「平面の上側」という言葉が意味を成しません。

それを克服するために、線形代数の知識を使います。原点を通る平面は以下のように内積の形で表現することができました。

\vec{w} \cdot \vec{x} = 0,

ただし

\vec{w} = 
\left(
\begin{matrix}
w_0 \\
w_1 \\
w_2
\end{matrix}
\right), 
\ 
\vec{x} =
\left(
\begin{matrix}
x \\
y \\
z
\end{matrix}
\right).

この$\vec{w}$を法線ベクトルと呼びましたが、これを平面で分割された空間を区別するものとして活用します。

便宜上、このページでは法線ベクトル$\vec{w}$の方向のことを「平面の上側」と呼びます。

例えば、平面の上側にあるベクトル$\vec{a}$と$\vec{w}$の内積を計算してみます。ここでは具体的な数値は問題ではなく、その内積の計算結果の正負にのみ注目します。

まず$\vec{a}$を$\vec{w}$と並行方向と垂直方向に分解します。$\vec{a}$の$\vec{w}$と垂直方向のベクトルを$\vec{a_{\perp}}$ 、$\vec{w}$と平行方向のベクトルを$\vec{a_{\parallel}}$ とかくと、以下のように表現できます。

\vec{a} = \vec{a_{\perp}} + \vec{a_{\parallel}}

.

ではこれと$\vec{w}$の内積を計算しましょう。

\begin{align}
\vec{w} \cdot \vec{a} &= \vec{w} \cdot (\vec{a_{\perp}} + \vec{a_{\parallel}}) \\
&= \vec{w} \cdot \vec{a_{\perp}} + \vec{w} \cdot \vec{a_{\parallel}} \\
&= 0 +  \vec{w} \cdot \vec{a_{\parallel}} \\
&= || \vec{w} || \ || \vec{a_{\parallel}} || \cos \theta
\end{align}

ここで$\theta$は0か$\pi$の値しかとりえません。従って$\cos \theta$は1か-1です。
そしてこの正負は、$\vec{a}$が$\vec{w}$と同じ方向を向いているか、あるいは反対方向を向いているかにのみ依存し、決まります。

長くなりましたが、まとめるとこうです。

  • 2次元のデータを3次元のデータに読み替える
  • 区別したい集団の間を分断させる平面をいいかんじに求める
  • 平面の式を内積の表現にする
  • その法線ベクトルと予測したいデータの内積を計算し、その符号が正ならば法線ベクトル方向にデータがある、負ならば法線ベクトルとは反対方向にデータがあると判断する

次は上に書いたいいかんじに平面を求める方法についてです。

ここではパーセプトロンの学習規則と呼ばれる手法を用いて平面を求めます。以下に説明をしますが、他にも下に書いたサイトや、パーセプトロンの学習規則でググってわかりやすいサイトを参照してください。（わかりやすいサイトがあったら教えてください。）(一番わかりやすいの -> [第2版]Python 機械学習プログラミング 達人データサイエンティストによる理論と実践 (impress top gear) のp21付近)

パーセプトロンの学習規則

ここではパーセプトロンの学習規則をもちいて、平面をいいかんじに求める方法について説明します。より具体的には、いいかんじに**法線ベクトル$\vec{w}$**を求める方法です。

まず初期値として$\vec{w_0}$をランダムに選びます。これからこのベクトルを$\vec{w_1}$, $\vec{w_2}$ ... と、徐々に更新して、目的となるいいかんじの法線ベクトルに近づけていきます。

次に更新の方法を説明します。

テストデータの一つのベクトル$\vec{x}$との内積$\vec{w_0} \cdot \vec{x}$を計算し、その正負を確認します。要するにテストデータに対して予測を行います。この予測が正しければ法線ベクトル$\vec{w_0}$を変更する必要はありません。なので$\vec{w_1}$は$\vec{w_0}$と同じでよいでしょう。一方、この予測が間違っている場合は法線ベクトルが間違っているので変更を加える必要があるでしょう。ここでは以下のように$\vec{w_1}$を更新します:

\vec{w_1} = \vec{w_0} + \nu l_{\vec{x}} \vec{x}

, ここで$\nu$は重みの程度を表すパラメータ, $l_{\vec{x}}$は$\vec{x}$に対応するラベル(つまり1か-1)です。$\nu > 0$であり、$\nu$が大きいほど、予測が間違えているときの修正が大きくなります。逆にこれが0に近いほど、予測が間違えていてもさほど修正しようとしません。

さて、上のように一つ更新された$\vec{w_1}$を得られました。

このあとは、上を繰り返して$\vec{w_2}, \ \vec{w_3}, \ \cdots$と法線ベクトルを更新していきます。適当な回数(10回なり10000回なり)繰り返したら止めてください。

実践問題

  • ★1. 上記の方法で、線形識別を実装する。
  • ★2. 冒頭のLength,Width,LabelのCSVデータを使って学習し、Length, Widthがそれぞれ11.0, 5.2である木材がどのように識別されるか試してみてください。
    1. sklearnのPerceptronで最初にいれた3つのパラメータmax_iter, eta0, random_stateのそれぞれの意味が何かを調べてみてください。
    1. ここで紹介した方法は空間2つに分割することにより分類を実現しています。しかしながら、このような方法では絶対に分類できないようなデータを考えることができます。それはどのようなデータでしょうか。 -> 線形分離可能・線形分離不可能 http://hokuts.com/2015/11/24/ml1_func/

触れようと思ったけどやめたこと

  • ニューラルネットワークの文脈からみた線形識別。このページで説明をしたものはニューラルネットワークのおなじみの図を用いて説明することができます。
  • 確率的勾配降下法
  • SVM

参考

0
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?