LoginSignup
17
12

More than 5 years have passed since last update.

@kenchon

PyTorch Tutorials 3/5

Last updated at Posted at 2018-01-20

注意！

PyTorch 0.4 以降、Variableは非推奨となり、Tensorに統合されました。

Welcome to the migration guide for PyTorch 0.4.0. In this release we introduced many exciting new features and critical bug fixes, with the goal of providing users a better and cleaner interface. In this guide, we will cover the most important changes in migrating existing code from previous versions:
・ Tensors and Variables have merged

よって、本記事の内容は一部サポートされていませんので、0.4向けに改変された元のTutorialを見てください！

本記事について

本記事は，前回の記事に引き続き，PyTorchチュートリアル(3/5)を動かしてみたノートです。

このノートは，公式ドキュメントに公開されている5つのチュートリアルのうちの３つ目：

  • Neural Networks

の日本語訳と，適宜説明を追加しています。

References:

ニューラルネットワーク

ニューラルネットワークはtorch.nnパッケージで構築することができます。
autogradは前回のチュートリアルで見たと思いますが，nnはモデルを定義したり，そのモデルの微分計算をするので，autogradに依存するパッケージです。
nn.Moduleには，層とメソッドforward(input)が含まれており，forward(input)はoutputをかえします。

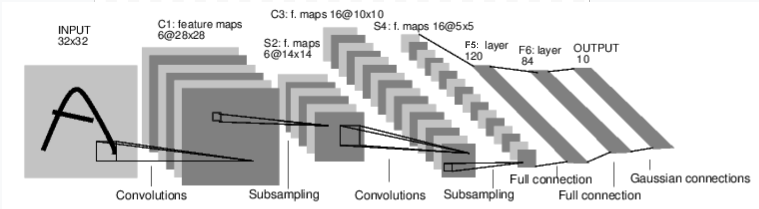
例えば，手書き文字を分類するニューラルネットワークを見てみましょう：

http://pytorch.org/tutorials/_images/mnist.png
convnet

これはシンプルな順伝播ネットワークです。つまり，リカレントニューラルネットワークのように，後の層の出力が前の層に戻ることがない，一方向のネットワークです。

ニューラルネットワークの学習は，大体次のような手続きで行います：

  • 学習可能なパラメータをもつニューラルネットワークを定義する。

  • データを入力し，入力のたびに学習を繰り返す。

  • 損失計算を行う。損失は，教師データと出力がどれだけ離れているかを示す。

  • 誤差逆伝播法による勾配計算

  • ネットワークのパラメータを更新する。更新式は，次式のようになる：

　　　　　　$w = w - \alpha \nabla L$

ネットワークを定義する

それでは，実際にネットワークを定義してみましょう：

import torch
from torch.autograd import Variable
import torch.nn as nn
import torch.nn.functional as F


class Net(nn.Module):

    def __init__(self):
        super(Net, self).__init__()
        # 1 input image channel, 6 output channels, 5x5 square convolution
        # kernel
        self.conv1 = nn.Conv2d(1, 6, 5)
        self.conv2 = nn.Conv2d(6, 16, 5)
        # an affine operation: y = Wx + b
        self.fc1 = nn.Linear(16 * 5 * 5, 120)
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)

    def forward(self, x):
        # Max pooling over a (2, 2) window
        x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
        # If the size is a square you can only specify a single number
        x = F.max_pool2d(F.relu(self.conv2(x)), 2)
        x = x.view(-1, self.num_flat_features(x))
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x

    def num_flat_features(self, x):
        size = x.size()[1:]  # all dimensions except the batch dimension
        num_features = 1
        for s in size:
            num_features *= s
        return num_features


net = Net()
print(net)

Net(
  (conv1): Conv2d (1, 6, kernel_size=(5, 5), stride=(1, 1))
  (conv2): Conv2d (6, 16, kernel_size=(5, 5), stride=(1, 1))
  (fc1): Linear(in_features=400, out_features=120)
  (fc2): Linear(in_features=120, out_features=84)
  (fc3): Linear(in_features=84, out_features=10)
)

forward関数を定義するだけで，backward関数は自動的に定義できます。このbackward関数というのは，勾配が計算される関数です。これがautogradの便利なところです。
forward関数では，Tensorに関する全ての演算を使うことができます。

学習可能なパラメータはnet.parameters()で確認できます。

params = list(net.parameters())
print(len(params))
print(params[0].size())  # conv1's .weight

10
torch.Size([6, 1, 5, 5])

forward関数の入力も出力も両方autograd.Variableです。
上記のネットワーク(LeNet)の入力は32×32なので，もしMNISTデータセットでこのネットワークを使うなら32×32にリサイズする必要があります。

全てのパラメータの勾配情報を溜め込んでいるバッファーを0にし，ランダムな勾配を逆伝播させるには：

input = Variable(torch.randn(1, 1, 32, 32))
out = net(input)
print(out)

Variable containing:
 0.0732  0.1061  0.1426 -0.1083 -0.0080  0.0531 -0.0105  0.0335 -0.0270  0.0096
[torch.FloatTensor of size 1x10]

Note:
torch.nnはミニバッチのみサポートしているので，単体のデータを利用できません。
例えば，nn.Conv2dは４次元テンソルnSamples x nChannels x Height x Widthを引数としてとります。単体のサンプルを入力するときは，input.unsqueeze(0)を使うことでバッチの次元をごまかすことができます。

一度，これまでのおさらいをします。

  • torch.Tensor - 多次元配列
  • autograd.Variable - Tensorのラッパーで，Tensorに行われた演算を記録する。Tensorと同様のAPIを持ち，backward()のような追加のメソッドなどもある。tensorに関する勾配情報も保持している。
  • nn.Module - ニューラルネットワークのモジュール。パラメータをカプセル化したり，パラメータをGPUに載せたり，出力したり，ロードしたりする便利な機能をもつ。
  • nn.Parameter - Variableの一種で，Moduleを定義した時に自動的に登録される。
  • autograd.Function - autogradの演算における順伝播と逆伝播の定義を実装したパッケージ。すべてのVariableの演算は，少なくとも１つのFunctionノードを作る。そしてこのノードは，Variableを生成した関数と結び付けられる。そしてこのノードが，演算の履歴を再現する。

ここまで，

  • ニューラルネットワークを定義する

  • 入力の処理とbackwardの呼び出し

について見てきました。

次に，

  • 損失の計算

  • ネットワークの更新

について見ていきます。

損失関数

損失関数は (output, target) という２つの入力を受け取り，outputがtargetとどれだけ離れているかを計算します。

nnパッケージには，いくつかの損失関数が実装されています。シンプルな損失関数として，nn.MSELossを取り上げてみます。これは，入力とターゲットの平均二乗誤差を計算するものです。

例えば，

output = net(input)
target = Variable(torch.arange(1, 11))  # a dummy target, for example
criterion = nn.MSELoss()

loss = criterion(output, target)
print(loss)

Variable containing:
 38.3841
[torch.FloatTensor of size 1]

以下は，lossがどのように計算されているかについてのフローです。

input  -> conv2d -> relu -> maxpool2d -> conv2d -> relu -> maxpool2d

       -> view -> linear -> relu -> linear -> relu -> linear

       -> MSELoss

       -> loss

loss.backwardを呼び出した時，計算フロー全体は損失に関して微分される。そして，フロー（グラフ中）のVariableは.gradVariableを持つ。

例として，損失関数から前の計算ステップにさかのぼってみましょう：

print(loss.grad_fn)  # MSELoss
print(loss.grad_fn.next_functions[0][0])  # Linear
print(loss.grad_fn.next_functions[0][0].next_functions[0][0])  # ReLU

<MseLossBackward object at 0x000002A1F10A1400>
<AddmmBackward object at 0x000002A1F10A1390>
<ExpandBackward object at 0x000002A1F10A1400>

逆伝播

誤差を逆伝播させるためには，loss.backward()するだけで良いです。
net.zero_grad()で勾配をすべて0にすることができますが，これを呼び出さなければ勾配は既存の勾配に蓄積されていきます。

それではloss.backward()を実際によびだして，その前後でconv1のバイアスの勾配がどのように変わるか見てみましょう。

net.zero_grad()

print('conv1.bias.grad before backward')
print(net.conv1.bias.grad)

loss.backward()

print('conv1.bias.grad after backward')
print(net.conv1.bias.grad)

conv1.bias.grad before backward
None
conv1.bias.grad after backward
Variable containing:
1.00000e-02 *
  9.6753
  9.1669
  2.7569
 -4.2307
  2.5546
 -2.6041
[torch.FloatTensor of size 6]

以上で，損失関数の扱い方を見てきました。

後で読みたい：

ニューラルネットワークのパッケージには，種々のモジュールと損失関数が用意されています。そしてそれらを組み合わせて深層ニューラルネットワークを構築します。それらのモジュールについてはこちら。

残っていること

  • ネットワークのパラメータの更新

パラメータの更新

最も簡単なパラメータ更新方法としては，確率的勾配降下法(SGD)が知られています。これは次の式で表現できます：
weight = weight - learning_rate * gradient

この更新規則は，次のコードで表現できます：

learning_rate = 0.01
for f in net.parameters():
    f.data.sub_(f.grad.data * learning_rate)

しかし，SGD以外にもNesterov-SGD, Adam, RMSPropなどのパラメータ更新法を適用したい人もいるでしょう。これを可能にするのがtorch.optimパッケージです。このパッケージにはすでにこれらの更新規則が実装されており，簡単に使うことができます。

import torch.optim as optim

# create your optimizer
optimizer = optim.SGD(net.parameters(), lr=0.01)

# in your training loop:
optimizer.zero_grad()   # zero the gradient buffers
output = net(input)
loss = criterion(output, target)
loss.backward()
optimizer.step()    # Does the update

次のチュートリアルへ

17
12
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
17
12