AutoEncoder, VAE, CVAEの比較 〜なぜVAEは連続的な画像を生成できるのか？〜

AutoEncoder（AE）、Variational AutoEncoder（VAE）、Conditional Variational AutoEncoderの比較を行った。
また、実験によって潜在変数の次元数が結果に与える影響を調査した。

はじめに

最近業務でVariational AutoEncoder（VAE）を使用したいなと勝手に目論んでおります。

そこでVAEの勉強するために、VAEの実装はもちろん、その元にあるAutoEncoder（AE）と、さらに発展系であるConditional Variational AutoEncoderの実装を行い、比較を行いました。

使ったのはフレームワークはもちろん（？）chainerです！！

そもそもVAEとは、GANなどと同じくDNNの生成モデルであり、画像生成を中心に現在研究が進んでいるところです。

では、GANとの大きな違いはなんなのか？
それは連続的に変化する画像を生成しやすいと言われています。
そこで、実験によって、なぜVAEは連続的に変化する画像を生成しやすいという特徴があるのか、調査しました。

本記事では、まずVAEの元にある、AutoEncoderのロジックの解説を行い、そののちに、VAEの説明を行います。

さらに、VAEの発展系であるCVAEの説明も行います。

説明の後にコードの紹介も行います。

また、AE, VAE, CVAEの違いを可視化するため、VAEがなぜ連続性を表現できるのか割り出すために、行った実験と、その結果について説明します。

ロジック

本記事は実験をメインとしているため、ロジックの説明は少々雑です・・・（すみません）

https://qiita.com/kenmatsu4/items/b029d697e9995d93aa24
https://www.slideshare.net/ssusere55c63/variational-autoencoder-64515581
https://deepage.net/deep_learning/2016/10/09/deeplearning_autoencoder.html

上記の記事が数式を踏まえてわかりやすくVAEのロジックについて説明してくれているので、気になる方は確認してみてください。

AutoEncoder（AE）

AutoEncoder（AE）とは、NNを用いて次元削減する手法です。

おそらく元の論文は2006年にかの有名なHintonが発表した下記の論文です。

Hinton, Geoffrey E., and Ruslan R. Salakhutdinov. "Reducing the dimensionality of data with neural networks." science 313.5786 (2006): 504-507.

年代的にDNNブームの元になった論文かな・・・？

ネットワークの構造は下記のようになっています。

AutoEncoderのネットワーク構造

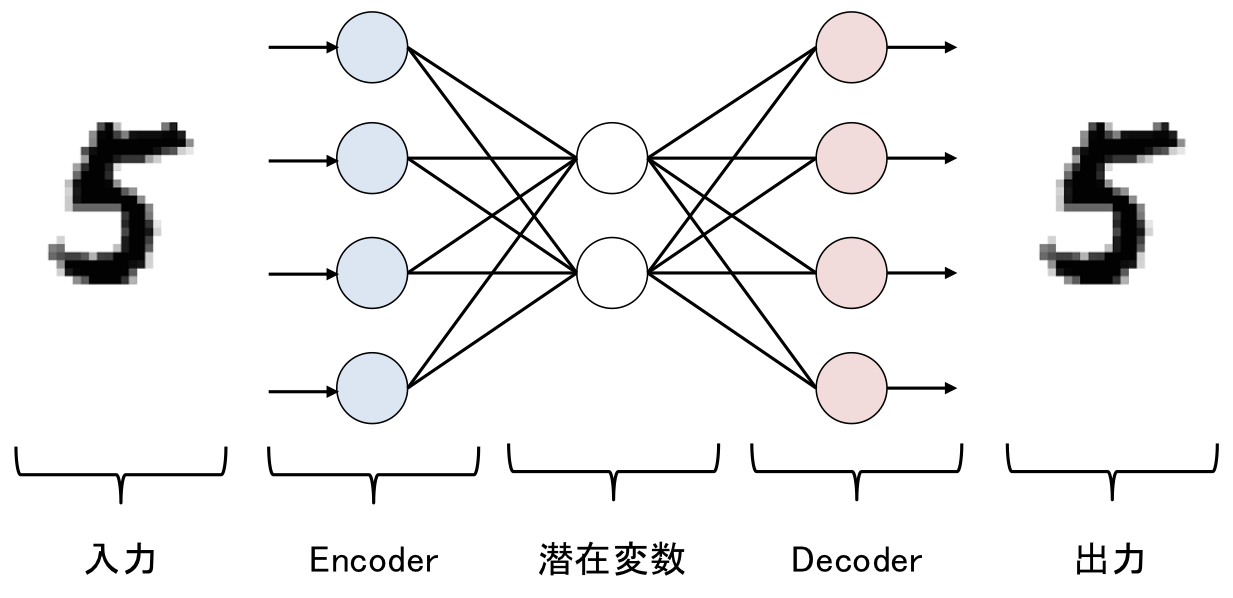AEはEncoderとDecoderの主に２つのパートからなっています。

Encoderでは、入力されたベクトル（図ではMNISの5）を次元圧縮を行います。

一方で、Decoderでは、圧縮されたベクトルから元の入力を再現しようとします。

元の入力と出力が同じになるようにネットワークを学習していくので、潜在変数は入力のデータの特徴量をできるだけ保持した形になります。

故にAEの潜在変数を抽出することで、次元削減として用いることができます。

Variational Auto Encoder（VAE）

潜在変数のサンプリング

AEは、いわゆる識別モデルというやつです。

AEの潜在変数部分に確率分布を導入したものがVariational AutoEncoder（VAE）になります。

VAEの元の論文は下記のものになります。
Kingma, Diederik P., and Max Welling. "Auto-encoding variational bayes." arXiv preprint arXiv:1312.6114 (2013).

分布を導入するとはどういうことぞや・・・？

まずはネットワーク図をお見せします。

Variational Auto Encoderのネットワーク構造

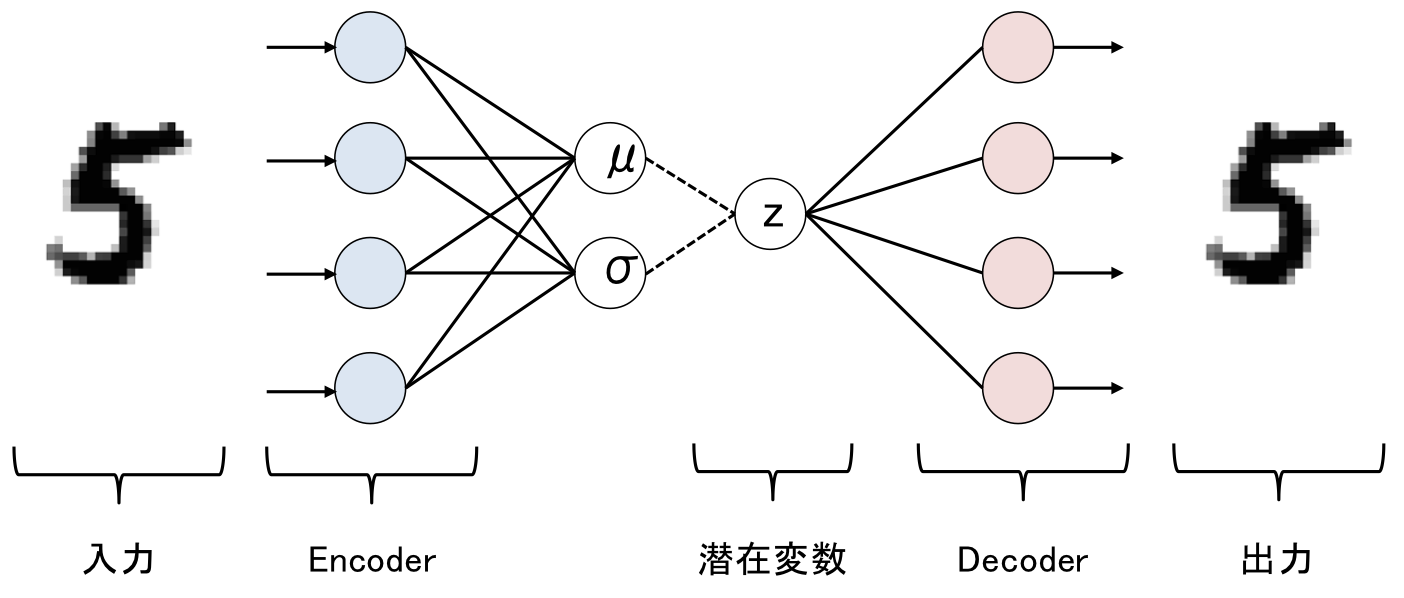VAEでは、Encoderを用いて、平均ベクトル$\mu$と分散ベクトル$\sigma$を求めます。

このようにして求めた平均ベクトル、分散ベクトルを元に、多変量ガウス分布から潜在変数$z$をサンプリングします。

z \sim N(\mu, \sigma)

VAEでは、サンプリングによって求められたベクトル$z$が次元圧縮後のベクトルとなります。

感覚的に解釈するなら、平均ベクトル$\mu$にある程度ランダム性を持たせて次元圧縮後のベクトル$z$を求めるイメージです。

Reparametrization Trick

しかし、このままではこのネットワークは学習ができません。なぜなら潜在変数をサンプリングしている時点でバックプロパゲーションができないからです。

そこで、Reparametrization Trickという技術が使われます。

$z$をサンプリングで求めるのではなく、下記のように近似します。

z = \mu + \epsilon \sigma 
(\epsilon \sim N(0, I))

なのでネットワーク構造は実際には下記のようになります。

Reparametrization Trick後のVAE

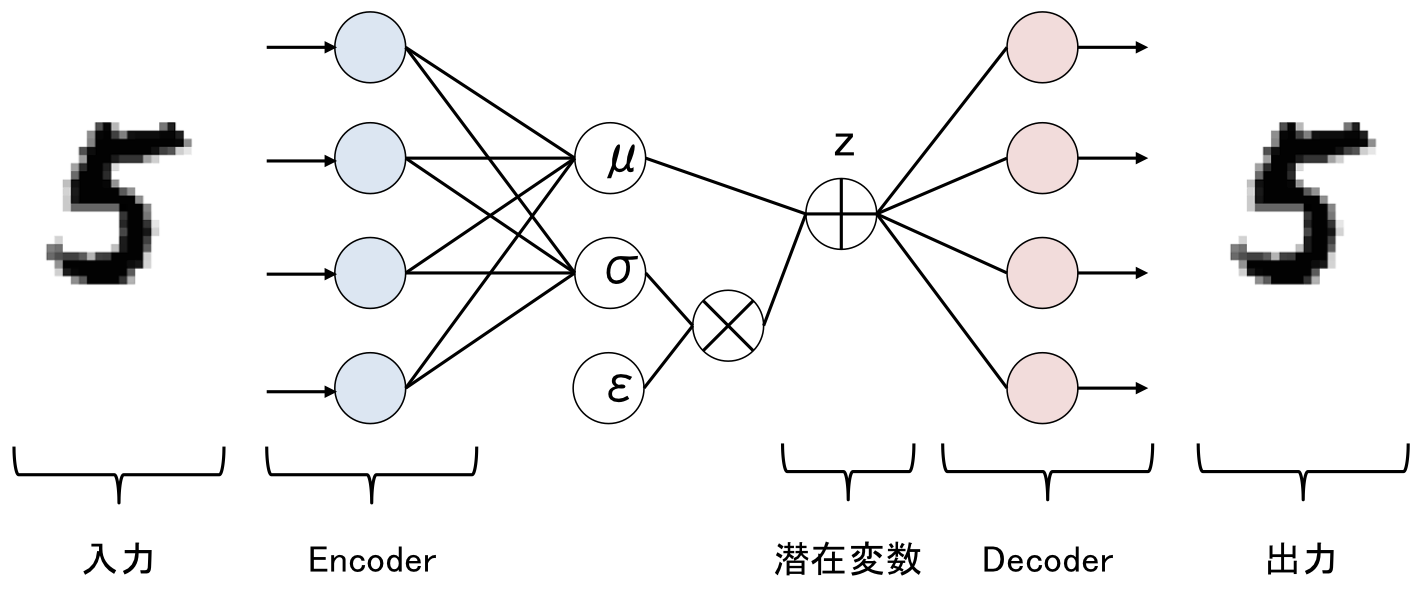Regularization Parameter（正則化項）

さて、VAEの学習時は、AEと同様に元の画像を復元しようとネットワークの学習を行います。

これはReconstraction Error（復元誤差）と呼ばれます。

しかしVAEでは、Reconstraction Errorだけでなく、Regularization Parameter（正則化項）の学習も行います。

Regularization Parameterの式は以下です。

\begin{align}
RegLoss &= -D_{KL}(q_{\phi}(z|x)|p_{\phi}(z)) \\
&= -D_{KL}(N(\mu, \sigma)|N(0, I))
\end{align}

$D_{KL}$はKLダイバージェンスを表しています。

つまり、Reconstraction Errorでは平均ベクトル$\mu$と分散ベクトル$\sigma$がなるべく原点を中心としたベクトルになるように学習を行うための項です。

この項により、VAEによって次元削減されたベクトルは、原点を中心に連続的に変化するベクトルになります。

Conditional Variational Auto Encoder（CVAE）

Conditional Variational Auto Encoder（CVAE）とは、VAEに対して正解ラベルを付与して学習を行います。

元論文は下記です。
Kingma, Diederik P., et al. "Semi-supervised learning with deep generative models." Advances in Neural Information Processing Systems. 2014.

CVAEのネットワーク構造は下記のようになります。

Conditional Variational Auto Encoderのネットワーク構造

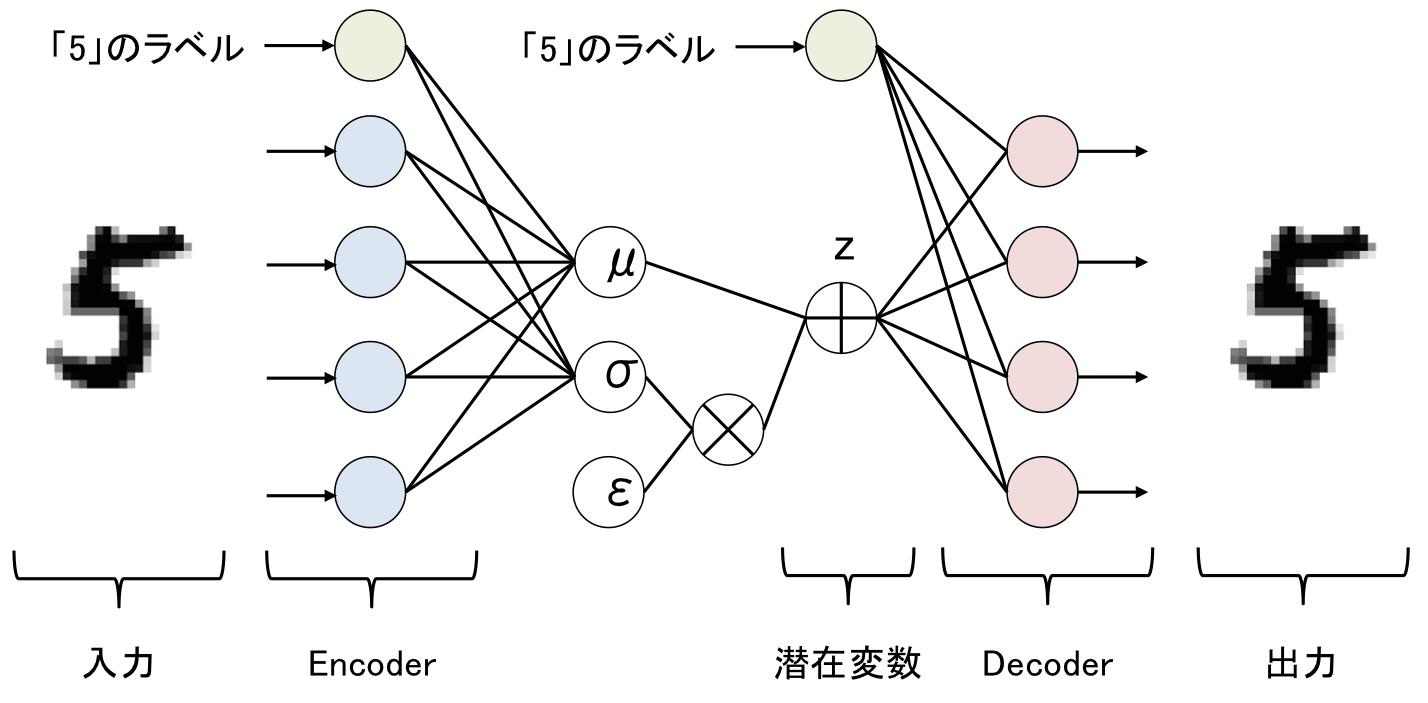VAEとの違いは、Encoder、Decoderに正解ラベルを付与するところです（図では数字の5とわかるようなラベルを付与）。

もちろん全てのデータに正解がある必要はなく、半教師ありで次元削減ができるというメリットがあります。

実装

Variational Auto Encoder（VAE）

VAEのchainerの実装を紹介します。

紹介といってもほぼ公式サンプルのままなのですが・・・

コードは下記にあります。
train部分
AutoEncoderモデル
VAEモデル
CVAEモデル
各モデルで使用しているXavierモデル

VAEのモデルは下記になります。

# coding: utf-8
"""
VAEのサンプルコード
Kingma, Diederik P., and Max Welling. "Auto-encoding variational bayes." arXiv preprint arXiv:1312.6114 (2013).
"""
import six

import chainer
import chainer.functions as F
from chainer.functions.loss.vae import gaussian_kl_divergence
import chainer.links as L

from sampleXavier import Xavier # Xavierはベクトル初期化の際の調整を行う手法

class VAE(chainer.Chain):
    """Variational AutoEncoder"""

    def __init__(self, n_in, n_latent, n_h):
        super(VAE, self).__init__()
        with self.init_scope():
            # encoder
            # 入力から隠れベクトルの作成
            self.le1 = L.Linear(n_in, n_h, initialW=Xavier(n_in, n_h))
            # 隠れベクトルから平均ベクトルの作成
            self.le2_mu = L.Linear(n_h, n_latent, initialW=Xavier(n_h, n_latent))
            # 隠れベクトルから分散ベクトルの作成
            self.le2_ln_var = L.Linear(n_h, n_latent, initialW=Xavier(n_h, n_latent))
            # decoder
            # 潜在変数から隠れベクトルの作成
            self.ld1 = L.Linear(n_latent, n_h, initialW=Xavier(n_latent, n_h))
            # 隠れベクトルから出力ベクトルの作成
            self.ld2 = L.Linear(n_h, n_in, initialW=Xavier(n_h, n_in))

    def __call__(self, x, sigmoid=True):
        """AutoEncoder"""
        # callされた時、EncodeしてDecodeした結果を返す
        return self.decode(self.encode(x)[0], sigmoid)

    def encode(self, x):
        # 入力ベクトルを隠れベクトルに変換して、tanhにかける
        h1 = F.tanh(self.le1(x))
        # 隠れベクトルを平均ベクトルに変換
        mu = self.le2_mu(h1)
        # 隠れベクトルを分散ベクトルに変換
        ln_var = self.le2_ln_var(h1)  # log(sigma**2)
        return mu, ln_var

    def decode(self, z, sigmoid=True):
        # 潜在変数を隠れベクトルに変換して、tanhにかける
        h1 = F.tanh(self.ld1(z))
        # 隠れベクトルを出力ベクトルに変換
        h2 = self.ld2(h1)
        if sigmoid:
            return F.sigmoid(h2)
        else:
            return h2

    def get_loss_func(self, C=1.0, k=1):
        """
        VAEの損失の計算
        Args:
            C (int): 正則化項をどれだけ効かせるかの変数、通常1.0が使用される
            k (int): サンプルを何回行うか
        """
        def lf(x):
            # 入力から、平均ベクトル、分散ベクトルの計算
            mu, ln_var = self.encode(x)
            batchsize = len(mu.data)
            # 復元誤差の計算
            rec_loss = 0
            for l in six.moves.range(k):
                z = F.gaussian(mu, ln_var)
                rec_loss += F.bernoulli_nll(x, self.decode(z, sigmoid=False)) \
                    / (k * batchsize)
            self.rec_loss = rec_loss
            # 正則化項の計算
            self.loss = self.rec_loss + \
                C * gaussian_kl_divergence(mu, ln_var) / batchsize
            chainer.report(
                {'rec_loss': rec_loss, 'loss': self.loss}, observer=self)
            return self.loss
        return lf

コード内にコメントアウトは極力書きましたが、ポイントはget_loss_funcの部分です。
学習時はCとkを変化させることで大分結果が変わります・・・

Conditional Variational Auto Encoder（CVAE）

CVAEのモデルは下記になります。

# coding: utf-8
"""
CVAEのサンプルコード
"""
import six

import chainer
import chainer.functions as F
from chainer.functions.loss.vae import gaussian_kl_divergence
import chainer.links as L

from sampleXavier import Xavier


class CVAE(chainer.Chain):
    """Conditional Variational AutoEncoder"""

    def __init__(self, n_in, n_latent, n_h, n_label):
        super(CVAE, self).__init__()
        with self.init_scope():
            # encoder
            # ラベルをベクトルに変換するためのembed
            self.embed_e = L.EmbedID(n_label, n_h, ignore_label=-1, initialW=Xavier(n_label, n_h))
            # 入力ベクトルから隠れベクトルに変換
            self.le1 = L.Linear(n_in, n_h, initialW=Xavier(n_in, n_h))
            # 隠れベクトルから平均ベクトルに変換
            self.le2_mu = L.Linear(n_h*2, n_latent, initialW=Xavier(n_h*2, n_latent))
            # 隠れベクトルから分散ベクトルに変換
            self.le2_ln_var = L.Linear(n_h*2, n_latent, initialW=Xavier(n_h*2, n_latent))
            # decoder
            # ラベルをベクトルに変換するためのembed
            self.embed_d = L.EmbedID(n_label, n_h, ignore_label=-1, initialW=Xavier(n_label, n_h))
            # 潜在変数から隠れベクトルに変換
            self.ld1 = L.Linear(n_latent, n_h, initialW=Xavier(n_latent, n_h))
            # 隠れベクトルから出力ベクトルに変換
            self.ld2 = L.Linear(n_h*2, n_in, initialW=Xavier(n_h*2, n_in))

    def __call__(self, x, sigmoid=True):
        # call時は、encodeを行い、平均ベクトルを潜在変数としてdecodeする
        return self.decode(self.encode(x)[0], sigmoid)

    def encode(self, x, y):
        # 入力ベクトルを隠れベクトルに変換
        h1 = F.tanh(self.le1(x))
        # ラベルをベクトルに変換後、tanhをかける
        h2 = F.tanh(self.embed_e(y))
        # 隠れベクトルとラベルベクトルを結合後、平均ベクトルに変換
        mu = self.le2_mu(F.concat([h1, h2]))
        # 隠れベクトルとラベルベクトルを結合後、分散ベクトルに変換
        ln_var = self.le2_ln_var(F.concat([h1, h2]))  # log(sigma**2)
        return mu, ln_var

    def decode(self, z, y, sigmoid=True):
        # 潜在変数を隠れベクトルに変換し、tanhにかける
        h1 = F.tanh(self.ld1(z))
        # ラベルをベクトルに変換後、tanhにかける
        h2 = F.tanh(self.embed_d(y))
        # 隠れベクトル、ラベルベクトルを結合後、出力ベクトルに変換
        h3 = self.ld2(F.concat([h1, h2]))
        if sigmoid:
            return F.sigmoid(h3)
        else:
            return h3

    def get_loss_func(self, C=1.0, k=1):
        """
        CVAEの損失の計算
        Args:
            C (int): 正則化項をどれだけ効かせるかの変数、通常1.0が使用される
            k (int): サンプルを何回行うか
        """
        def lf(x, y):
            mu, ln_var = self.encode(x, y)
            batchsize = len(mu.data)
            # reconstruction loss
            rec_loss = 0
            for l in six.moves.range(k):
                z = F.gaussian(mu, ln_var)
                rec_loss += F.bernoulli_nll(x, self.decode(z, y, sigmoid=False)) \
                    / (k * batchsize)
            self.rec_loss = rec_loss
            self.loss = self.rec_loss + \
                C * gaussian_kl_divergence(mu, ln_var) / batchsize
            return self.loss
        return lf

VAEとの違いは、encoder、decoderにラベルを読み込ませ、EmbedIDでベクトルに変換後、それぞれのネットワークにかけている点です（あまり自信ないです、間違ってたらすみません・・・）。

実験

本章ではこれまでに説明したAutoEncoder（AE）、Variational AutoEncoder（VAE）、Conditional Variational AutoEncoder（VAE）を用いて実験を行います。

実験の大きな目的は、2つあり、1つは各モデルの精度を比較すること、
もう1つは、潜在変数の次元数が結果に与える影響を可視化し、なぜVAEが連続した画像を生成しやすいという特性を持っているのかを調べることです。

実験準備

データセット

実験に用いたデータセットはMNISTです。

trainデータには784次元(28×28)のベクトルが全部で60000枚分、
testデータには同じ次元のベクトルを2000枚分使用しました。

CVAEでは、trainデータのうち30000枚には正解ラベルを付与し、残りの30000枚にはラベルを付与しない、半教師あり学習を行いました。

実験概要

行った実験は4種類です。

潜在変数の次元数が与える影響を可視化するために、それぞれの実験では、複数の潜在変数の次元数で学習したモデルを使用しています。

下記に実験の概要をまとめます。

	タイトル	概要
実験1	復元	AE, VAE, VCAEの学習後のモデルにテストデータを入力して、数字がどの程度復元されるのかを比較 またCVAEに関しては、正解ラベル付与なし、正解ラベル付与、正解ではないラベルを付与した時に、復元される数字の比較をおこなった
実験2	連続変化	学習済みのVAEのモデルを用いた。 数字$X$と数字$Y$をそれぞれ潜在変数$Z_x$, $Z_y$に変換後、$Z_x$->$Z_y$へと変化する連続する潜在変数を作成する 作成した潜在変数から数字を復元した際に、どのように数字が変化して行くのかを確認した
実験3	プロット	AE, VAE, CVAEの学習後のモデルを用いた。 それぞれのモデルを用いて、testデータを潜在変数に変換。 得られた潜在変数をマッピングし、各数字がどのようにマッピングされているのかを確認した
実験4	クラスタリング	AE, VAE, CVAEの学習後のモデルを用いた。 それぞれのモデルを用いて、testデータを潜在変数に変換。 得られた潜在変数をKmeansでクラスタリングし、v-scoreでクラスタリングの精度を比較した。 分割するクラスタ数は10に固定し、それぞれのモデルで５０回クラスタリングを行い、精度を測定。 測定された精度のばらつきを箱ひげグラフで比較した。

学習条件

Z_SIZE（潜在変数の次元数）を2, 4, 16, 64の4パターンに変えて学習しています。

それ以外のパラメータは極力共通になるようにモデルを作成しています。

	AE	VAE	CVAE
INPUT_SIZE	784	784	784
HIDDEN_SIZE	128	128	128
EMBED_SIZE （正解ラベルをベクトルに変換した時のサイズ）	-	-	128
Z_SIZE	2, 4, 16, 64	2, 4, 16, 64	2, 4, 16, 64
MINIBATCH_SIZE	100	100	100
C (lossを計算する際のparam)	-	0.1	0.1
k (lossを計算する際のparam)	-	5	5
EPOCH_NUM	1000	1000	1000

実験1（復元）

実験1ではAE, VAE, CVAEを用いて数字がどの程度綺麗に復元されるのか確認しました。

CVAEに関しては、正解ラベルを付与していない時、正解ラベルを付与した時、間違ったラベルを付与した時で比較をしています。

また、Z_SIZEが4, 16, 64の時で結果を比較しています。

数字の「4」と「2」を復元させました。

元の画像

数字の4	数字の2

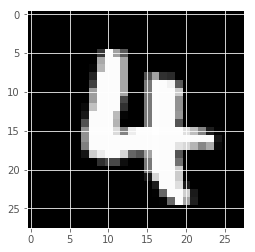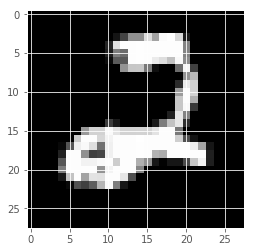数字「4」の復元結果

	$Z\_SIZE=4$	$Z\_SIZE=16$	$Z\_SIZE=64$
AE
VAE
CVAE（ラベルなし）
CVAE（ラベル「4」）
CVAE（ラベル「9」）

数字「2」の復元結果

	$Z\_SIZE=4$	$Z\_SIZE=16$	$Z\_SIZE=64$
AE
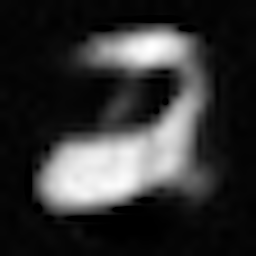VAE
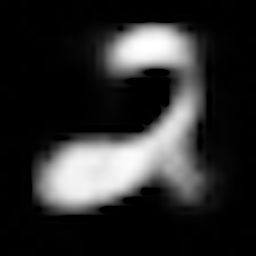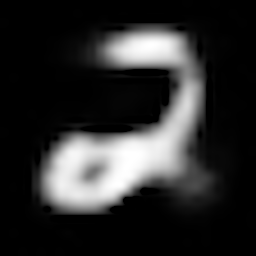CVAE（ラベルなし）
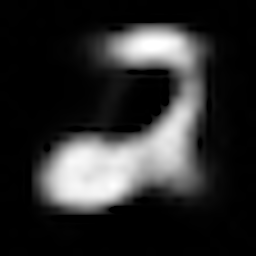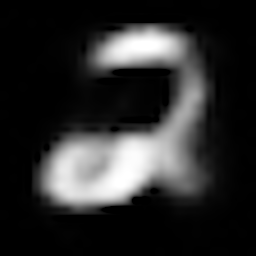CVAE（ラベル「2」）
CVAE（ラベル「7」）

復元結果より、いずれのモデルもZ_SIZEが大きい方がより鮮明に元の画像を復元できていることがわかります。
例えば、「4」の例では、次元数が小さい時は、数字の9になっています。

このことから、潜在変数の次元数が小さい時は、他の数字になりやすいことがわかります。

また、AEよりも、VAE, CVAEの方が綺麗に画像を復元できています。

CVAEの結果だけに注目すると、一番綺麗に復元できているのは、やはり正解ラベルを付与した時の結果です。

反対に、間違ったラベルを付与した時は、付与したラベルに復元結果がよっていることもわかります（特に4の時は、9になっている）。

実験2（連続変化）

実験2では、学習済みのVAEを用いて、数字を連続的に変化させてみました。

モデルは、Z_SIZEを4, 16, 64の3種類のもので比較しました。

試した例は、「1」から「0」への変化、「3」から「7」の2パターンです。

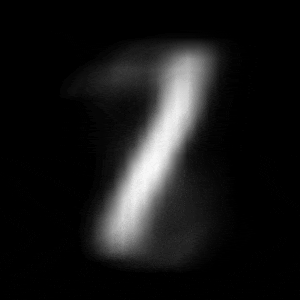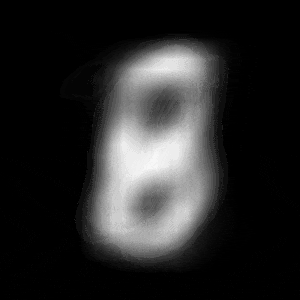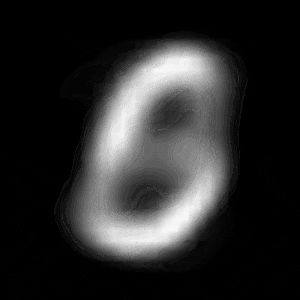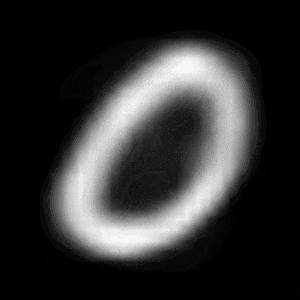
パターン1 （「1」->「0」）

$Z\_SIZE=4$	$Z\_SIZE=16$	$Z\_SIZE=64$

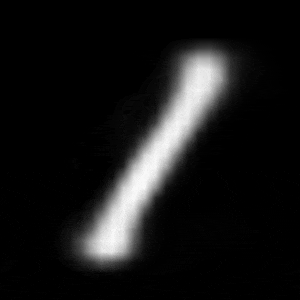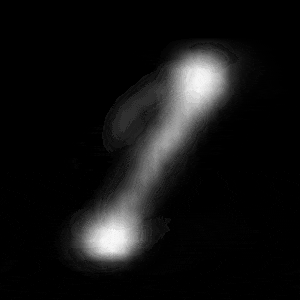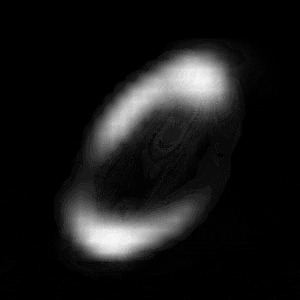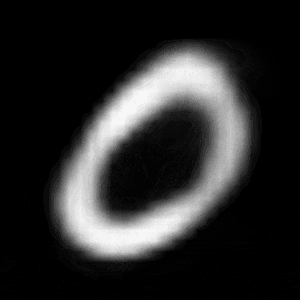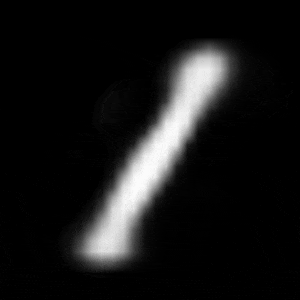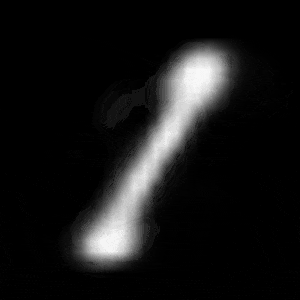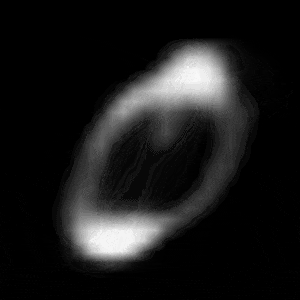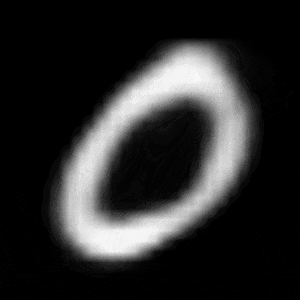パターン2 （「3」->「7」）

$Z\_SIZE=4$	$Z\_SIZE=16$	$Z\_SIZE=64$

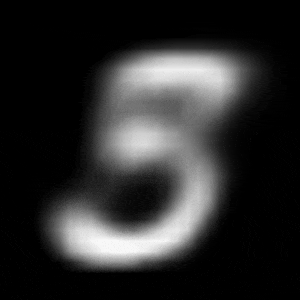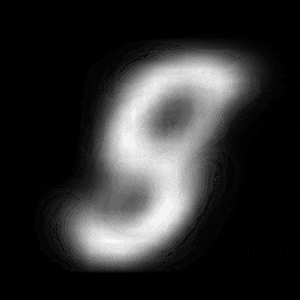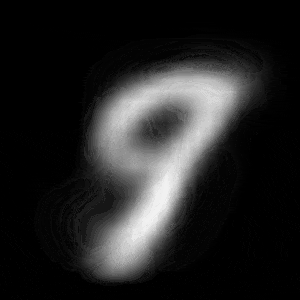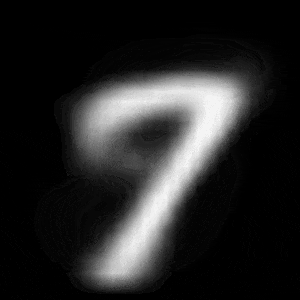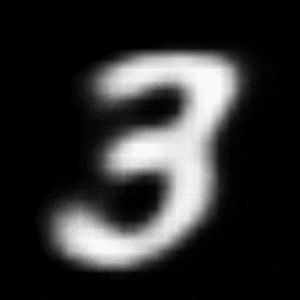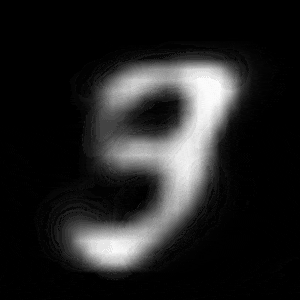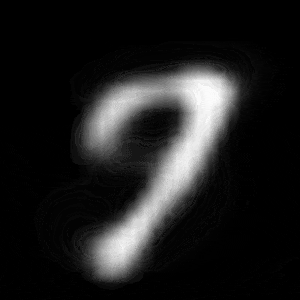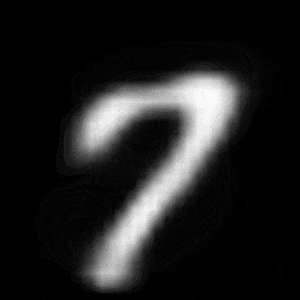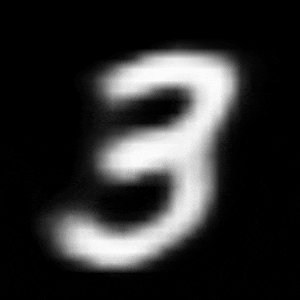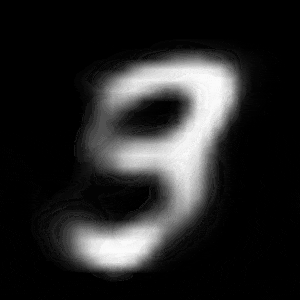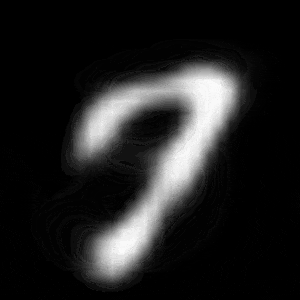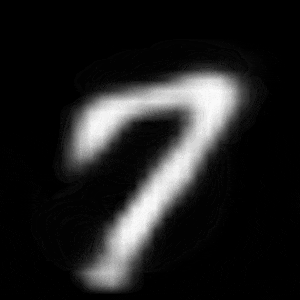異なる潜在変数の次元で試したのですが、潜在変数の次元数が小さいほど、数字の変化が激しいことがわかります。

例えば、パターン1では、次元数が4の時は、「1」->「8」->「6」->「0」と変化しているのに対して、次元数が64の時は、「1」 -> 「0」と変化しています。

同様に、パターン2では、次元数が4の時は、「3」->「8」->「9」->「7」と変化しているのに対して、次元数が64の時は、「3」->「9」->「7」と変化しています。

これは実験1の結果と同様に、潜在変数の次元が小さい方が、他の数字になりやすいことに起因しているからだと考察できます。

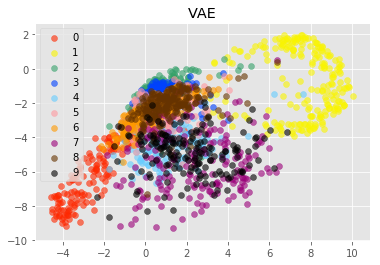
実験3（プロット）

実験3では、学習済みのAE, VAE, CVAEのモデルを用いて、testデータを潜在変数へと変換しました。

変換した潜在変数を数字ごとに異なる色でプロットしました。

モデルのZ_SIZEは2次元のものを使用しています（2次元にプロットしたかったため）。

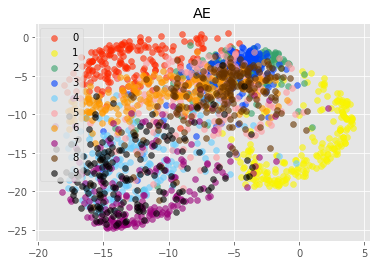
プロット結果

AE	VAE	CVAE

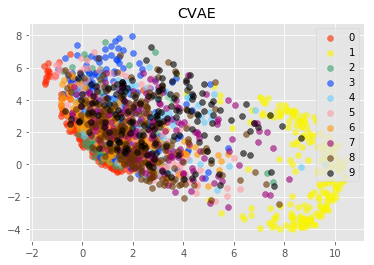プロット結果から見るに、AEの方が、VAEやCVAEと比較して、各数字ごとに異なる座標に次元圧縮できているように見えます。

注目して欲しいのは、座標の中心です。

AEではプロット結果が、x座標が-10, y座標が-10を中心としているのに対して、VAE, CVAEではどちらとも0に近い値を中心としているのがわかります。

これは学習時の損失関数に正則化項を加えているからだと考えられます。

正則化項は、潜在変数のばらつきを抑えています。
これによってVAE, CVAEでは、数字間で共通した特徴が、1つの次元で表現されやすくなっているのではないかと思います（そのせいで、各数字の潜在変数が綺麗に分かれていませんが・・・）。

これが、連続的な変化を表現できるというVAEの特性の元なのではないかと考えられます。

実験4（クラスタリング）

実験3では、VAE、CVAEでは、正則化項のおかげで、数字間で共通した特徴が、1つの次元で表現されやすくなっているのではないかということを確認しました。

一方で、2次元の潜在変数では、AEの方が各数字の特徴をより鮮明に表現していたとも言えます。

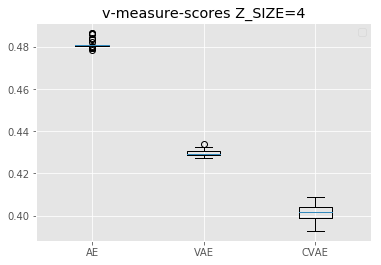
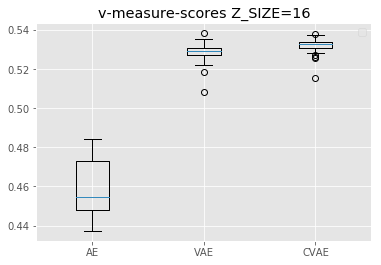
実験4では、各モデルにおいて、圧縮した潜在変数をクラスタリングしました。
さらに、定量的な評価指標でクラスタリングの精度を比較しました。
その結果、潜在変数のサイズが特徴の表現に与える結果を可視化しました。

それぞれのモデルで、Z_SIZEが4, 16, 64時の結果を比較しています。

クラスタリングの精度比較結果

$Z\_SIZE=4$	$Z\_SIZE=16$	$Z\_SIZE=64$

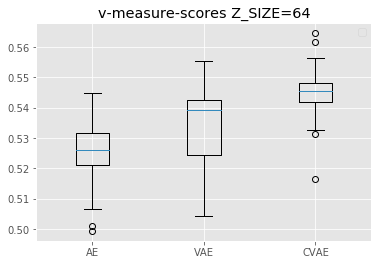グラフ内では、左から順にAE, VAE, CVAEの精度を表しています。

面白いのは、Z_SIZE=4の時と、Z_SIZE=16の時でAEと、VAE, CVAEの精度が逆転しているところです。

これは、実験3で2次元にプロットした時にAEの方が各数字ごとに綺麗に分かれていたことに起因すると考えられます。

VAE, CVAEでは正則化項のために、ラベルが中心に集まりやすくなりますが、次元数を増やすことで、射影できる範囲が広くなり、十分に各数字の違いをプロットできるようになっているのだと思います。

また、高次元になるとVAE、CVAEの方がAEよりも潜在変数が各数字の特徴をうまく表現できているということが言えます。
これは、実験1で、高次元の方が復元結果が鮮明であったことの理由だと考えられます。

また、VAEよりもCVAEの方が精度が高いことから、学習にラベルを含める効果も見てとることができます。

まとめ

本記事では、AutoEncoder, Variational AutoEncoder, Conditional Variational AutoEncoderの説明を行い、またそれぞれの特徴を4つの実験によって比較しました。

実験1では、AEよりも、VAEやCVAEの方が鮮明な画像を復元できることを示しました。
潜在変数の次元数が大きい方が、より綺麗な画像を復元できました。
また、CVAEの、正解ラベルを付与した時の方が、画像が鮮明になり、違うラベルを付与した時は、その数字に近くなるという特徴を確認しました。

実験2では、VAEの、連続的に変化する画像を生成できるという特徴を確認しました。
また、潜在変数の次元数が小さい時の方が、連続的に画像が変化するということも示しました。

実験3では、潜在変数の2次元へのプロットを行うことで、AE, VAE, CVAEの潜在変数の違いを可視化しました。
VAE、CVAEの方は、正則化項のおかげで、各数字が中心にプロットされることで、数字の連続性を表現しやすくなっていることを確認しました。

実験4では、潜在変数のクラスタリングを行いました。
その結果、低次元ではAEの方が、各数字の特徴をうまく表現できている一方で、高次元では、VAEやCVAEの方が、各数字の特徴をうまく表現できていることがわかりました。

まとめると、VAEは正則化項のおかげで潜在変数の連続性がうまく表現できるようになっています。
また、VAEの連続性を表現したいなら、潜在変数の次元数は小さい方が良いともいえます。
一方で、次元数が小さすぎると復元結果がよくないという事象も起きます。
つまり、VAEの学習の際は、ちょうどいい潜在変数のサイズを割り出すということが重要ということです。

参考文献

https://qiita.com/kenmatsu4/items/b029d697e9995d93aa24
https://www.slideshare.net/ssusere55c63/variational-autoencoder-64515581
https://deepage.net/deep_learning/2016/10/09/deeplearning_autoencoder.html