トピックモデルを操作 ~Interactive Topic Model~

Interactive Topic Modelの実装、及びその結果

はじめに

自然言語処理の技術で、文書集合から内容を抽出する方法としてトピックモデルという考え方がある。

その中でも、トピック内で出現する単語を意図的に操作する方法として、Interactive Topic Modelというものが存在する。

そこで、本記事ではInteractive Topic Modelの実装とその効果の検証を行う。

手法

トピックモデル

トピックモデルでは文書集合から、トピック（例えば、新聞記事には政治やスポーツなどのトピックが含まれていると推測される）が出現する確率、トピック分布$\theta$と、そのトピック内でどのような単語が出やすいか、単語分布$\phi$を推定する手法である。

トピックモデルの説明は、
http://qiita.com/GushiSnow/items/8156d440540b0a11dfe6
http://statmodeling.hatenablog.com/entry/topic-model-4
あたりの資料がわかりやすいので参照してください。

Latent Dirichlet Allocation（LDA）

様々あるトピックモデルの中でも、Latent Dirichlet Allocation（LDA）が一番有名である。

LDAでは、1つの文書（新聞記事）の中に、複数のトピックが存在（政治やニュースなど）し、それぞれのトピックが異なる単語分布を持つと考える。

グラフィカルモデルは下記の図の通り

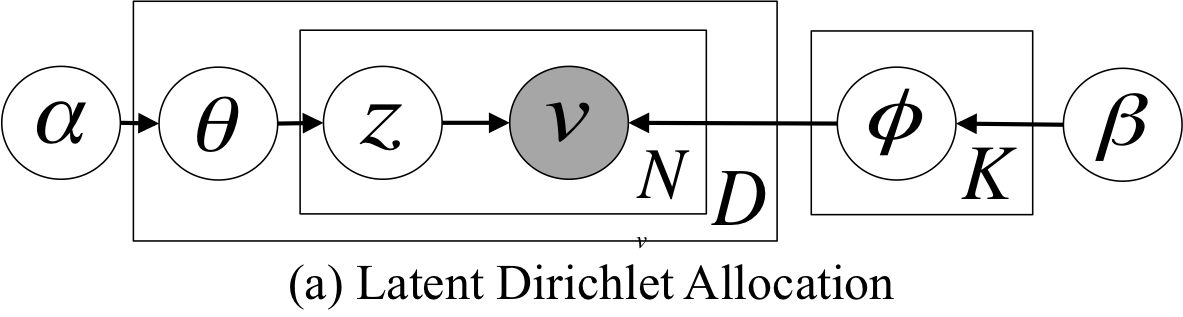
ちなみに$\theta$はトピック分布、$\phi$は単語分布、$z$は文書内の単語に割り当てられるトピック、$v$は文書内の単語、$N$は文書内の単語数、$D$は文書数、$K$はトピック数、$\alpha$、$\beta$はハイパーパラメータです。

LDAの計算には、ギブスサンプリングや、変分ベイズが使えるが、崩壊型ギブスサンプリング（CGS）が一番有名？である。

崩壊型ギブスサンプリングでLDAを計算する際の疑似コードは下記の通り

N_dk = 0  # 文書d内でトピックkが割り当てられている単語の数
N_kv = 0  # トピックk内で単語vが出現した回数
N_k = 0   # トピックkが割り当てられた単語の数
d = 1, …, D  # 文書番号
k = 1, …, K  # トピック番号
v = 1, …, V  # 語彙番号

initialize(z_dn)  # 文書d内、n番目の単語のトピックをランダムに初期化

repeat
  for d = 1, …, D do
    for n = 1, …, N_d do # N_dは文書d内で使用されている単語数

      N_d[k=z_dn] -= 1  # カウントから引く
      N_[k=z_dn][v=w_n] -= 1
      N_[k=z_dn] -= 1

      for k = 1, …, K do
        cal(p(z_dn = k)) # 文書d内のn番目の単語にトピックkが割り当てられる確率を計算
      endfor

      z_dn ~ Categorical(p(z_dn))  # z_dnのトピックをサンプリング

      N_d[k=z_dn] += 1  # 新しく割り当てられたトピックをカウント
      N_[k=z_dn][v=w_n] += 1
      N_[k=z_dn] += 1

    endfor
  endfor
until 終了条件を満たすまで

疑似コード内の$p(z_{dn} = k)$になる確率を計算は、以下のようにする。

p(z_{dn}=k) \propto (N_{dk}+\alpha)\frac{N_{kw_{dn}}+\beta}{N_k+\beta V}

で計算できる。

Interactive Topic Model（ITM）

LDAでトピックの計算をすると、この単語とこの単語は一緒のトピックになって欲しいのに・・・ということがある。

この問題に対して、単語Aと単語Bは同じトピックから出るようにしてください、と制約をかけることで取り組むことができる。

それがInteractive Topic Model（ITM）
http://dl.acm.org/citation.cfm?id=2002505

感覚的な説明をすると、ITMでは、制約をかけた単語同士を1つの単語と考え、その単語の出現確率を等分配することで、制約をかけた単語同士を、同じトピックで出やすくする。

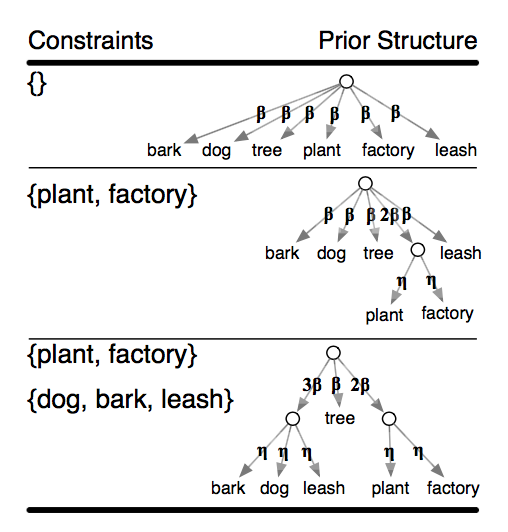
※ Interactive Topic Modelの論文より

計算は簡単で、LDAの$p(z_{dn} = k)$を計算する式を以下のように書き換える。

p(z_{dn} = k) \propto \begin{cases}
(N_{dk}+\alpha)\frac{N_{kw_{dn}}+\beta}{N_k+\beta V} \;\;\;\;(w_{dn} \notin \Omega)\\
(N_{dk}+\alpha)\frac{N_{k\Omega}+|\Omega|\beta}{N_k+\beta V}\frac{W_{k\Omega w_{dn}}+\eta}{W_{k \Omega} + |\Omega|\eta} \;\;\;\;(w_{dn} \in \Omega)

\end{cases}

ただし、$\Omega$は制約であり、$|\Omega|$は制約内に含まれる単語数、$N_{k\Omega}$はトピック$k$で制約$\Omega$が出てきた回数、$W_{k\Omega w_{dn}}$はトピックkに割り当てられた制約$\Omega$の中で単語 $w_{dn}$が出てきた回数を表している。

つまり、単語 $w_{dn}$が制約$\Omega$に含まれていなければ、LDAと同じ式で、含まれていたら下の式でp(z_{dn} = k)を計算すれば良い。

実験

実験ではITMの精度検証を行う。

データセット

データセットには、livedoorコーパスを用いた。http://bookmarks2022.blogspot.jp/2015/06/livedoor.html

コード

ITMのコードはここに
https://github.com/kenchin110100/machine_learning/blob/master/sampleITM.py

実験結果

トピック数 $K = 10$、$\alpha = 0.1$、$\beta = 0.01$、$\eta = 100$に固定

まずは制約なしで50iteration分（つまり普通のLDAと同じ）

各トピック内での出現単語の上位は下記の表の通り

トピック1	トピック2	トピック3	トピック4	トピック5
機能	アプリ	女性	作品	日本
発売	搭載	ゴルフ	映画	更新
更新	画面	自分	153	関連
記事	smartphone	男性	181	世界
利用	発表	結婚	監督	人気
デジ	対応	多い	公開	映画
関連	マックス株式会社	相手	3	http://
smartphone	Android	仕事	96	自分
ソフトウェア	表示	クリスマス	13	話題
ユーザー	2012年	女子	本	すごい

これだけでもそれなりのトピックが見れます。

次に表内の青地の単語が同じトピックになるように制約をかけて
さらに50iteration回します。

トピック1	トピック2	トピック3	トピック4	トピック5
発売	アプリ	女性	153	映画
利用	搭載	自分	181	日本
機能	smartphone	ゴルフ	3	作品
更新	発表	男性	96	公開
記事	対応	結婚	13	世界
サービス	ま	多い	552	監督
関連	マックス株式会社	相手	144	関連
デジ	Android	仕事	310	特集
ソフトウェア	表示	クリスマス	98	http://
情報	2012年	いい	ヒーロー	すごい

制約をかけた青文字の単語がトピック5に共通して出現していますね。

まとめ

Interactive Topic Model（ITM）により、単語に制約をかけてトピック分布の推定をしました。

載せた内容は一見良さそうに見えますが、実は何回のトライアンドエラーした結果・・・

ITMはジャーナルも出ているので、そっちの内容を実装すればもっと精度が良くなるかもしれませんね。