トピックモデルは応用範囲が広く、使えるところが多いモデルですが・・
数式が鬼難しく分かりづらいので、なるべく数式を使わずに分かりやすくしたい。
そして備忘録にしたいってことで記事を書きました。
間違いがあれば指摘して頂けると幸いです。
トピックモデルの使える範囲
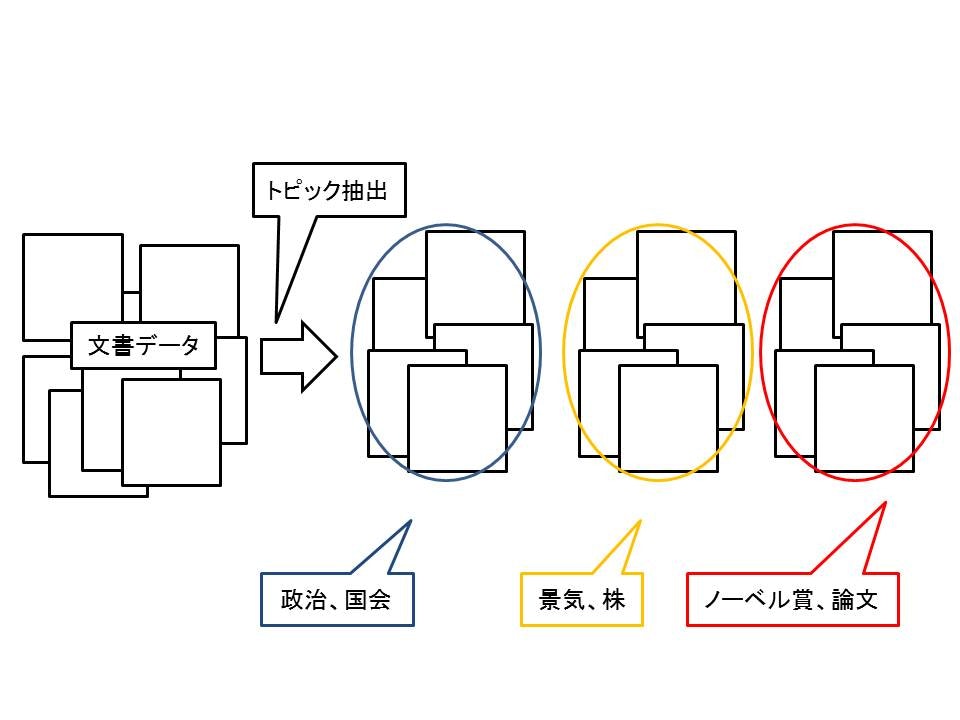
端的に言えば、文書からそれが何について記述されているかを推定するモデルです。
実は適用範囲はトピックを抽出をしていくだけではないです。
トピックに分けるだけでなく、文書の補助情報に関連付けをさせたり、ユーザーの情報に依存させたトピックのみに限定したり、トピックに相関関係を持たせたりできます。
また文書だけでなく、画像、ソーシャルネットワーク、論文の引用関係にも応用可能です。
トピックモデルの仕組み
重要な点をいくつか先に述べます。
確率分布、共役事前分布、パラメータ推定の3点がかなり重要になってきます。
1:確率分布
確率の分布なのですが、なぜこれが重要かといいますと、確率は試行回数が多くないと確定できないからです。
例えば、1回だけ宝くじを引いて、1等の1億円があったからと言って、宝くじで当たる確率は100%だとは言いません。
理想的には試行回数と言って、宝くじを多く引けば引くほど宝くじが当たる確率は真の確率に近くなります。
ですが宝くじを無限回引けと言われても厳しいのが現実です。
僕らエンジニアも同様の問題と立ち向かう必要があります。
例えば、”限られたデータでユーザーの行動を予測してよ”とか枚挙にいとまがありません。
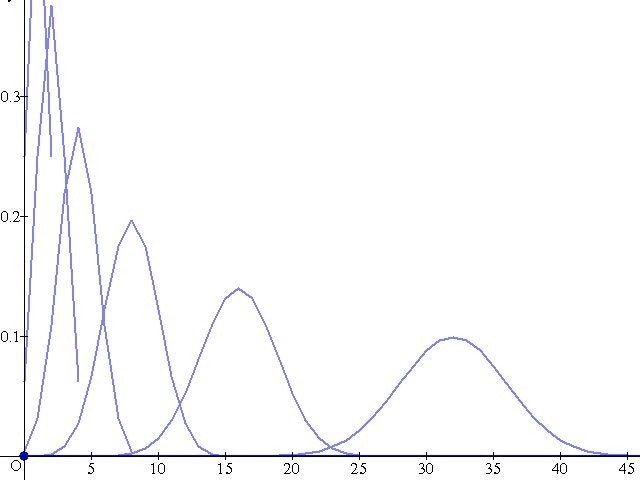
そこで役に立つのが確率分布です。
これは適用する事象によって異なりますが、先人達が作ってくれたいくつかの分布を適用することにより、少ないデータでもおおよその確率の予測がたつのです。
今回のトピックモデルで使用する分布しか紹介しませんが、他にも有用な分布はあるので、ドメインによって使い分けて下さい。
2値を扱う場合:ベルヌーイ分布
複数のトピックを扱う場合(トピックがありかなしかの{0,1}離散値):カテゴリ分布
カテゴリ分布のパラメータ推定に使用:ディリクレ分布
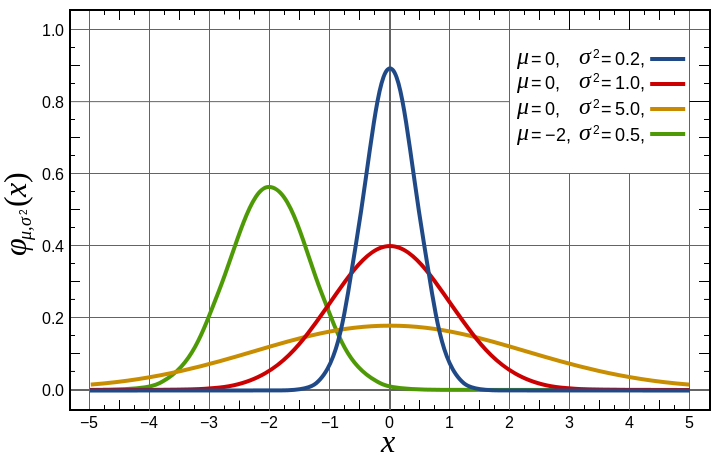
相関関係を測るのに使用:正規分布
2:共役事前分布
共役事前分布とは事前分布と事後分布が同じタイプになる分布のことです。
なんじゃそりゃと思われる方がいらっしゃると思います。
分布の重要性は先ほどの記述で述べたので、事前分布と事後分布について述べたいと思います。
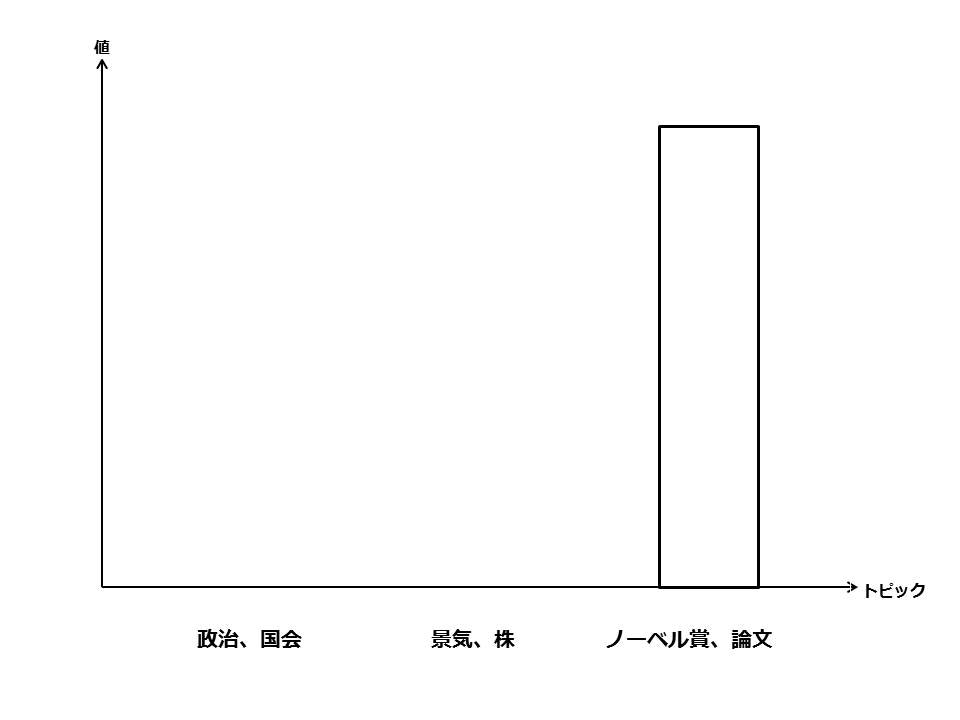
トピックモデルで求めたいのは文書のトピックです。
つまり事後分布が求まれば、事後分布から文書のトピックが生成されるのでできるだけ正確な事後分布を求めたいわけです。
事前分布と事後分布の形が異なっていた場合は解析的に求めることは困難です。
共役事前分布とは事前分布と事後分布が同じタイプになる分布なので、この共役事前分布を使用することでトピックが生成される確率分布が求めやすくなるわけです。
3:パラメータ推定
ここでいうパラメータとは事後分布のパラメータになります。
事後分布のパラメータが正確に求まれば、文書からのトピックをできるだけ正確に推定できる事後分布が作成できるわけです。
パラメータ推定の方法は複数あります。
代表的な3つの手法について、ご紹介します。
用語説明
尤度:観察データの下での仮説のもっともらしさ
最尤推定:事前確率を使用せずに尤度のみでパラメータを推定
ベイズ推定:今取得したデータだけでなく、過去の推定結果や経験に基づく事前確率も使用してパラメータを推定
1:EMアルゴリズム
対数尤度が最大となるパラメータを逐次的に求める手法
解説記事
http://yagays.github.io/blog/2013/12/15/mlac-2013-em-algorithm/
2:変分ベイズ推定
パラメータの更新方法はEMアルゴリズムと同様
事前分布と事後分布がKLダイバージェンスで最小となるように計算
解説記事
http://www.ism.ac.jp/~daichi/paper/vb-nlp-tutorial.pdf
3:ギブスサンプリング
複数のパラメータがある場合は崩壊型ギブスサンプリングを行います。
これは一つのパラメータのみベイズを用いた事後確率で算出し、他のパラメータは周辺化して固定する手法です。
周辺化したパラメータはサンプリングによって算出されたパラメータによって算出します。
解説記事
http://d.hatena.ne.jp/hoxo_m/20140911/p1
上記の手法を用いてトピックモデルの推定の説明に入ります。
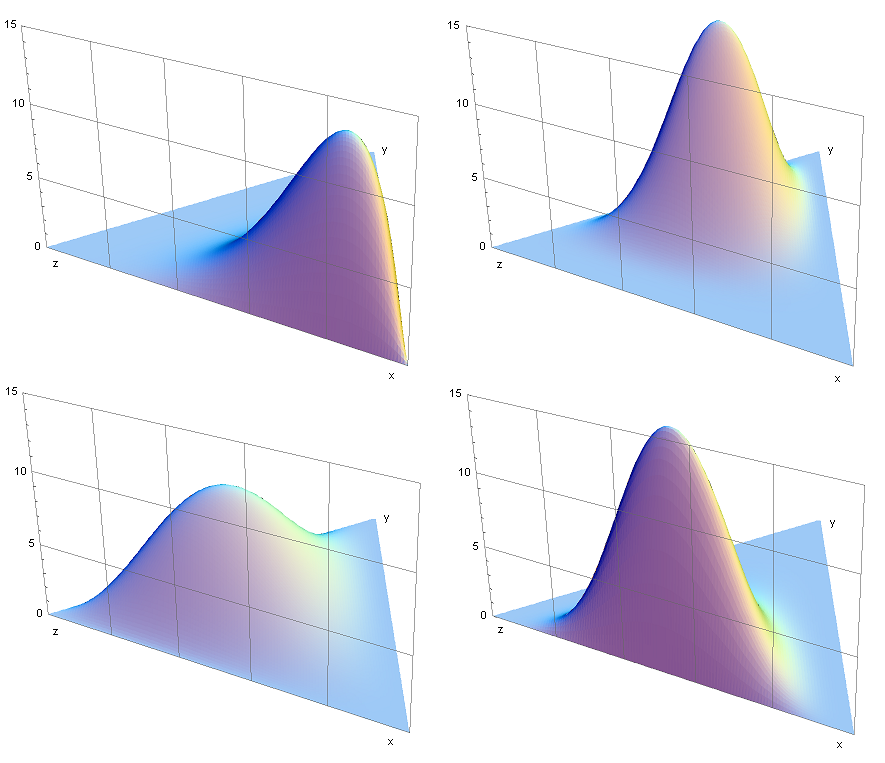
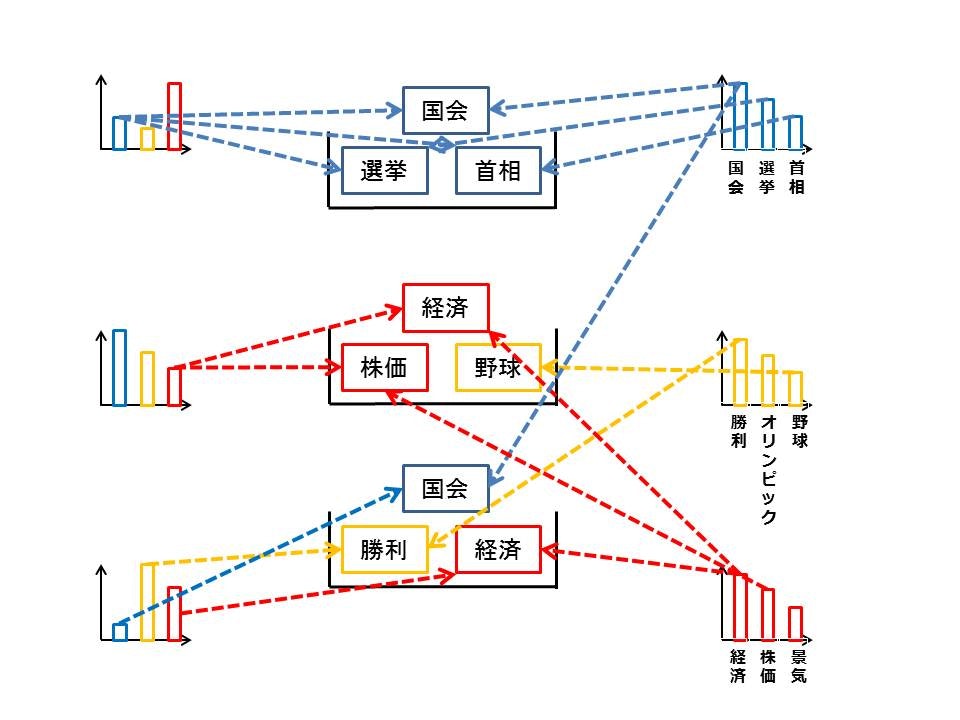
上図のように文書ごとのトピック分布と単語ごとのトピック分布を設定することで文書ごとに複数のトピックを含んだモデルを設定できます。
1:For トピック k = 1,...K
(a)単語分布を生成(ディリクレ分布を使用)
2:For 文書 d = 1,...D
(a)トピックを生成(カテゴリ分布を使用)
(b)単語を生成(カテゴリ分布を使用)
グラフィカルモデル(変数の依存関係が分かる図)
パラメータ更新(最尤推定、変分ベイズ推定(LDA)、ギブスサンプリング)
の3種類から選定し、パラメータを更新する。
データがたくさんあるよ、けど確率分布はどんなのか分からない
最尤推定:膨大なデータがあれば、より真の値に近くなる
データの数が微妙だけど確率分布は分かるぜ
変分ベイズ推定:事前分布が与えられているため、過学習しづらく観測数が少ない場合に有効
データないし事後確率分布も分からない
ギブスサンプリング:崩壊型ギブスサンプリングを用いるとパラメータの周辺化が可能なので求めるパラメータは一つに固定して、ベイズの法則を利用して得られる事後確率によって導出されたサンプルを利用してパラメータ更新(試行回数を増やせば真の分布に近づいていくが真の分布かどうか不明)
ギブスサンプリング資料
http://ebsa.ism.ac.jp/ebooks/sites/default/files/ebook/1881/pdf/vol3_ch10.pdf
トピックモデルは発展系もあるので、それは別記事で解説します。