前回の記事での改善をしていきます。前回の記事では彦根市の明日の天気を予測するために過去の彦根市の天気を使いました。今回は複数地点の天気の過去データを用いてどれだけ精度が上がるかやってみました。
使用したデータ
このページから彦根、神戸、美浜、奈良、岐阜の五地点から6月1日から7月1日までのひと月間のデータを2008年から2018年までの10年分使用しました。使用した項目は風向、最高気温、最低気温、平均気温、風速、降水量を使用しました。
データの整形
とりあえずデータに含まれる品質情報と品質番号はいらないので削除しました。それと、風向のデータがいくつか欠損してました。特に美浜の風向の項目はすべてのデータが欠損していました。観測自体実施されていないんでしょうか?それから、いくつかの地点で2008年6月24日までの風向のデータが欠損していました。この風向のデータはまとまった欠損だったので2008年6月24日までのデータは予測に使わないことにしました。美浜の風向は存在を消しました。
風向は16方位なのでダミー変数にしました。
import numpy as np
import pandas as pd
df_org=pd.read_csv("kakuti.csv",encoding="shiftjis",header=2).drop([0,1],axis=0).reset_index(drop=True)
# 降水量の合計以外は二個置きに残してあげればいい
drop_columns = ["最高気温(℃)","最低気温(℃)","平均風速(m/s)","平均現地気圧(hPa)","最多風向(16方位)"]
drop_ls = []
for i in drop_columns:
for j in range(1,15):
if j % 3 != 0:
drop_ls.append(i + "." + str(j))
df = df_org.drop(drop_ls,axis = 1)
# 降水量の合計で消すやつの番号
doropnum = [1,2,3,5,6,8,9,10,12,14,13,16,17,18]
df = df.drop(["降水量の合計(mm)." + str(i) for i in doropnum],axis = 1)
# すべて欠損値なのでやむなく消す
df = df.drop(["平均現地気圧(hPa).3"],axis = 1)
# 上から24個は風向が欠損値なので消す
df.drop(index=[i for i in range(24)], inplace=True)
# 風向をダミー変数に
label = ["最多風向(16方位)","最多風向(16方位).3","最多風向(16方位).6","最多風向(16方位).9","最多風向(16方位).12"]
for i in label:
df = pd.concat([df, pd.get_dummies(df[i], prefix=i)], axis=1)
for i in label:
del df[i]
教師データの作成
前回もそうでしたが、雨が降るか降らないかの二値分類を行います。六月は洗濯物干せる日が少ないのでぴったり当てたいです。
# データの作成
ans_ls = [0 for i in range(len(df))]
for i in range(24,len(df)+24):
s = df['降水量の合計(mm).15'][i]
if float(s) == float(0):
ans_ls[i-24] = 1
else:ans_ls[i-24] = 0
data_conp = []
for i in range(len(df)):
y,m,d = df.iloc[i,0].split('/')
if int(d) == 1 or m == '7':continue
if int(y) == 2008 and int(m) == 6 and int(d) <= 24:continue
data_conp.append([])
ls = data_conp[-1]
ls.append(ans_ls[i+1])
for k in range(i-1,i):
for j in range(len(df.columns) - 1):
ls.append(df.iloc[k+1,j+1])
# 目的変数と説明変数へ分割
y = np.array([0]*len(data_conp))
x = np.array([np.array([0.0 for i in range(len(data_conp[0]) - 1)]) for i in range(len(data_conp))])
for i in range(len(data_conp)):
for j in range(len(data_conp[0])):
if j == 0:
y[i] = data_conp[i][j]
else:
x[i][j-1] = data_conp[i][j]
めちゃめちゃコードが長くなってしまったんですけど、やっていることは雨が降るかどうかの0,1とそれの前日の天気の情報が同じ列に来るようにしてます。data_conpのあとの塊は正直無駄な部分が多いなと思っております。また改善ができるといいです。
機械学習にやつにデータをぶち込む
# 機械学習のやつ
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.preprocessing import StandardScaler
import warnings
warnings.filterwarnings('ignore')
clf = 0 # 書き方がわからなかった
def score_logistic(x,y,convLs = None,c = 1,job = 1,pena = "l1"):
global clf
scoreMean_train = 0
scoreMean_test = 0
ss = StandardScaler()
x = ss.fit_transform(x)
for i in range(30):
if convLs == None:
x_train, x_val, y_train, y_val = train_test_split(x, y, stratify=y, train_size=0.8)
else:
x_train, x_val, y_train, y_val = train_test_split(x[:,convLs], y, stratify=y, train_size=0.8)
clf = LogisticRegression(C = c,n_jobs = job,penalty = pena)
clf.fit(x_train, y_train)
y_train_pred = clf.predict(x_train)
y_val_pred = clf.predict(x_val)
train_score = accuracy_score(y_train, y_train_pred)
test_score = accuracy_score(y_val,y_val_pred)
#print('{}回目のスコア : {}'.format(i+1,train_score))
scoreMean_train += train_score
scoreMean_test += test_score
#print('組み合わせ : {} 十回の平均 : {}'.format(convLs,scoreMean / 10))
return (convLs,scoreMean_train / 30,scoreMean_test / 30)
簡単に関数を実行するだけで30回の平均を見たいからこんな関数を書きました。ほぼ前回のやつからの使いまわしです。途中あるclfという変数、ロジスティック回帰の係数を見たいけどうまく書く方法がわからなかったのでこんな感じになってます。よりよい方法があれば教えていただきたいです。とりあえずデータを入れてみます。
num = 0
for i in y:
if i == 1:num += 1
num/len(y)
# 0.581081081081081
mean = 0
for i in range(100):
mean += score_logistic(x,y,c = 0.1,pena = 'l1')[2]
mean /= 100
print(mean)
# 0.6309666666666668
パラメータはいろいろやってみてよさげな奴です。特徴量が多いのでl1正則化のほうが結果はいいかなと思ったんですけど、あまり結果は変わりませんでした。yに含まれる1の割合は大体0.58でした。一応5%程高くはなってます。前回の全く予測できない状況よりは改善しているかなあとは思います。しかし、やはり風向をダミー変数にしたのでデータ数に対して特徴量がえげつないほど多くなっています。これが原因かなと思ったので、主成分分析をしてみます。
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
# 主成分分析
pca = PCA()
pca.fit(x)
ev_ratio = pca.explained_variance_ratio_
ev_ratio = np.hstack([0,ev_ratio.cumsum()])
plt.plot(ev_ratio)
plt.show()
# データを主成分空間に写像
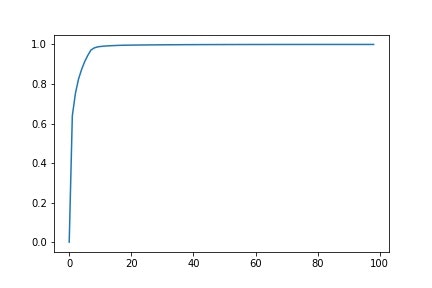
上のグラフは累積寄与率の変化です。さすがsklearn、主成分分析も一瞬でした。めちゃめちゃ便利です。このグラフを見ると、10次元でほぼほぼ説明できそうです。(実際には9次元で行う場合が精度が一番出ました。)
# 主成分分析
make_pca = PCA(n_components = 9)
make_pca.fit(x)
feature = make_pca.transform(x)
# ロジスティック回帰に突っ込む
print(score_logistic(feature,y,c = 1,pena='l2'))
# (None, 0.677542372881356, 0.6516666666666666)
# 100回の平均を算出
mean = 0
for i in range(100):
mean += score_logistic(feature,y,c = 1,pena = 'l2')[2]
mean /= 100
print(mean)
# 0.6469444444444445
1%ちょい精度が上がりました。この上昇が果たしてよいのか悪いのか、経験の浅い私にはわかりません。(というか機械学習なんて今年の春休みに勉強し始めたばっか)ただ、過学習は抑えることができました。これ以上は改善の方法がぱっと思いつかないのでひとまずこの話題はこれで終わろうと思います。もし改善の方法が他にあるようでしたら教えていただきたいです。