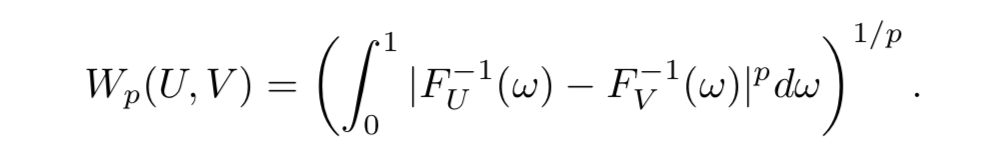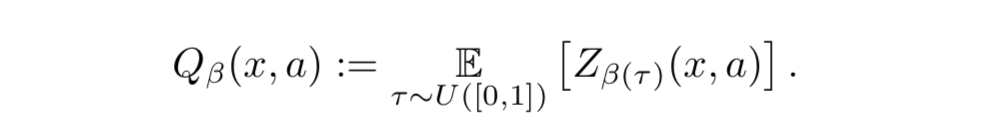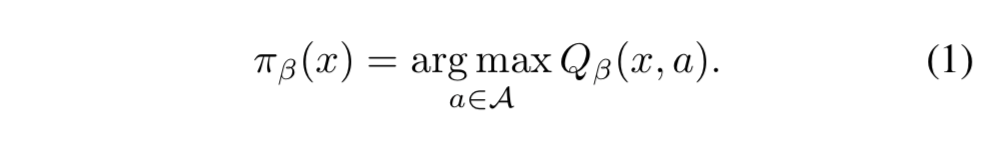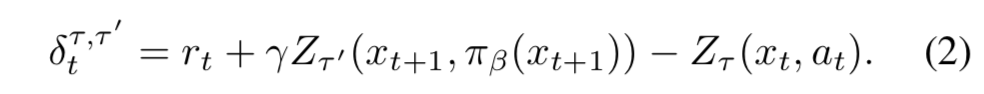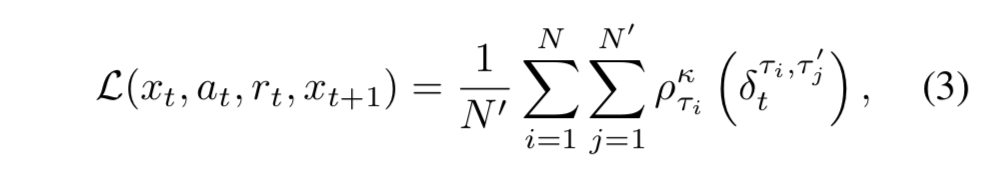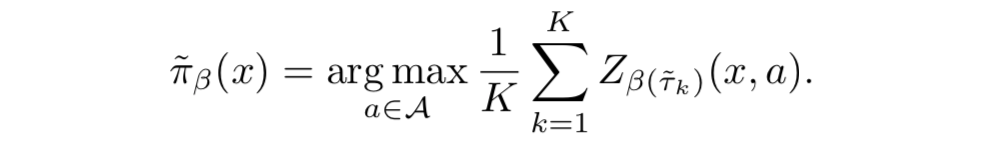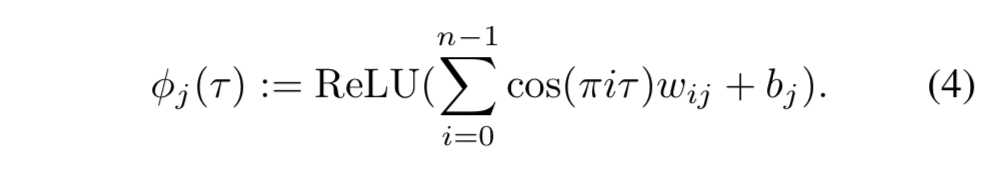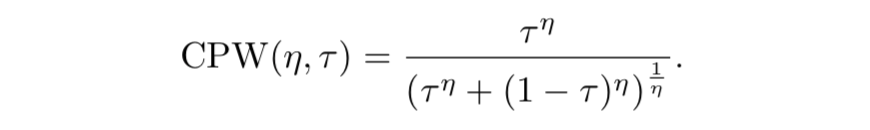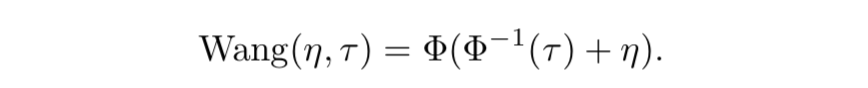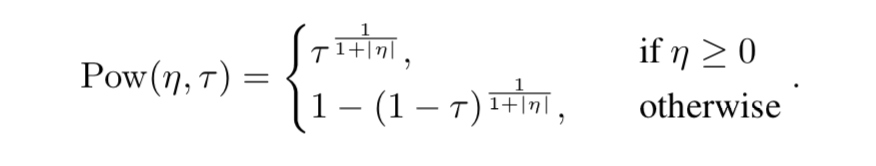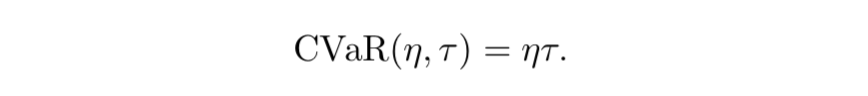【論文】Implicit Quantile Networks for Distributional Reinforcement Learning (IQN; 2018)

[1806.06923] Implicit Quantile Networks for Distributional Reinforcement Learning

メタ情報

• ICML 2018
• DeepMind

概要

• Distributional DQN を発展させた手法を提案する
  • 状態行動価値の分布を分位点回帰 (quantile regression) によって近似する

導入

• Distributaional RL は、環境・エージェント間のインタラクション、エージェント側の表現の近似、内在する物理的なカオス等のランダム性をモデル化することを試みている
• Distributaional RL は2つの側面で語ることができる：報酬分布のモデル化方法と、距離の定義。
  • Categorical DQN (C51, 2017) は報酬分布を「事前に範囲を決めたヒストグラム」、距離を「Cramer-minimizing projection と cross entropy」で定義
  • QR-DQN (2018) は報酬分布を「位置を分位点回帰で調整したディラック関数の mixture」¹ 、距離を「Wasserstein 距離」で定義
  • 提案法 IQN は QR-DQN を拡張した
    • 有限個の分位点の学習から分位点関数全体、つまり価値分布関数の学習へ
• DQN の単純な拡張である IQN の Atari-57 における性能向上は Rainbow に比肩する

背景/関連研究

• (RL の定式化の説明。略)

Distributional RL

• (distributional RL の定式化の説明。略)

p-Wasserstein Metric

• p-Wasserstein metric は累積分布関数の逆関数上の $L_p$ metric：
  • 

Distributional RL と分位点回帰

• [1707.06887] A Distributional Perspective on Reinforcement Learning で distributional ベルマン作用素が p-Wasserstein metric で縮小写像であることが示された
  • [1710.10044] Distributional Reinforcement Learning with Quantile Regression では適切な設定での分位点回帰が distributional ベルマン作用素が ∞-Wasserstein metric で縮小写像になることに帰結することを示した
  • [1802.08163] An Analysis of Categorical Distributional Reinforcement Learning ではカテゴリカルアルゴリズムが Cramer distance (累積分布関数の L2 metric) で縮小写像になることを示した

RL のリスク分析

• これまでの distributional RL では方策は価値関数分布の期待値に基づいていた
  • 方策も分布の情報を活用できるだろうか？(risk-sensitive な方策)

Implicit Quantile Networks

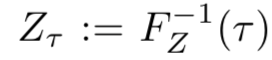• が確率変数 $Z$ の分位点 $\tau \in [0, 1]$ を返す関数とする
  • よって $\tau \sim U([0,1])$ とすれば、行動価値分布は $Z_\tau (x,a) \sim Z(x,a)$ となる
• $\beta: [0,1] \rightarrow [0,1]$ を distortion risk measure として、 $Z(x,a)$ を $\beta$ で歪ませた期待値 (distorted expectation) は次で与えられる：
  • 
• すると、risk-sensitive greedy 方策は
  • 
• 時刻 $t$ での方策 $\pi_\beta$ における TD 誤差のあるサンプルは、 $\tau, \tau^\prime \sim U([0,1])$ として
  • 
• これらの TD 誤差サンプルを適当な数集めて平均を取ったものが IQN の誤差関数：
  • 
    • ただし $\rho$ は 2.3 節で紹介した分位点回帰のロス
• 実際には $\pi_\beta$ の期待値計算 ² はできないので $K$ 個のサンプルで近似する：
  • 

実装

• DQN のネットワーク構造を利用
  • $\psi: \mathcal{X} \rightarrow \mathbb{R}^d$ を畳み込み層の関数、 $f: \mathbb{R}^d \rightarrow \mathbb{R}^{|\mathcal{A}|}$ をその後の全結合層の関数とする。つまり、 $Q(x,a) = f(\psi(x))_a$
• IQN ではこれに加えて $\phi: [0,1] \rightarrow \mathbb{R}^d$ を導入して $\tau$ の embedding を計算させ、 $Z_\tau (x,a) = f(\psi(x) \odot \phi(\tau))_a$ とする
  • $\odot$ は要素積 (アダマール積)
• 事前に実験をおこない、 $\phi$ の式を次のようにした ( $n$ は embedding の次元) (Appendix を参照) ³：
  • 
• また、式(3)における $\tau, \tau^\prime$ をサンプルする数 $N, N^\prime$ についても実験を行った：

• $N, N^\prime$ は大きくするほど良いが、長い目で見た性能 (Fig.2 右) から IQN では $N=N^\prime=8$ で十分であるとわかった
  • $N=N^\prime=1$ の場合であっても DQN よりも3倍性能が良い
• あまり影響がなかったため $K=32$ (方策近似のサンプル数) とした

Risk-sensitive 強化学習

• distortion risk measure $\beta$ に関する実験
  • $\beta$ が直接影響を与えるのは $\pi_\beta$
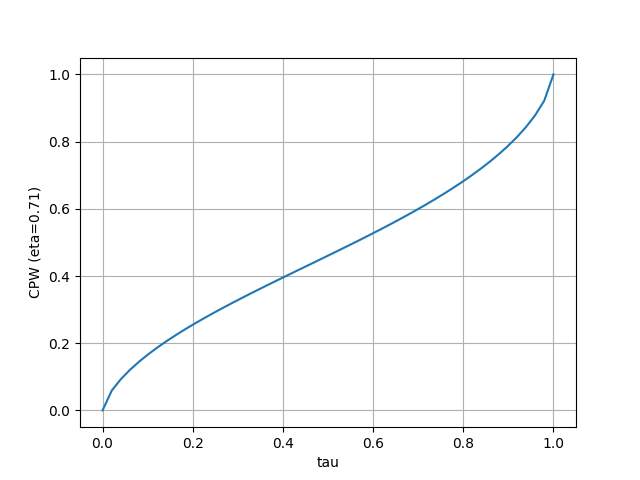
• Cumulative probability weighting
  • 
  • 
  • 人間に近い設定となるらしい $\eta = 0.71$ に設定
  • $\tau$ の小さな部分で局所的に上に凸 (リスクに鈍感 risk-averse)、大きな部分で局所的に下に凸 (リスクに敏感 risk-seeking)
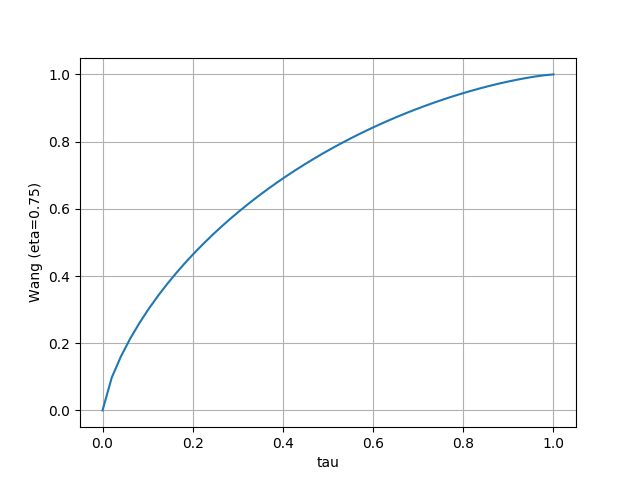
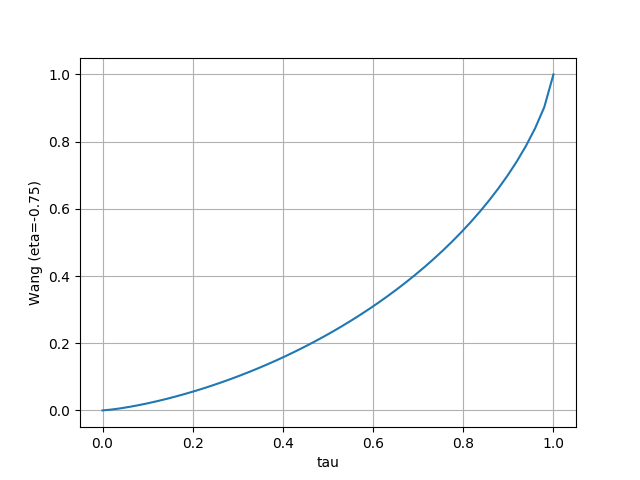
• Wang
  • 
  • $\Phi$ は標準正規分布の累積分布関数
  • 
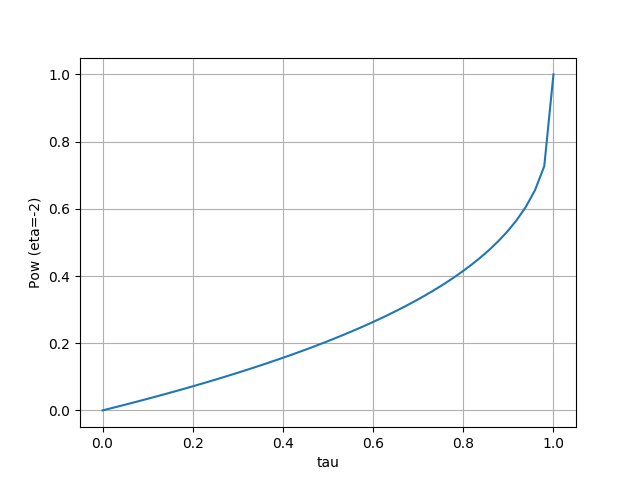
• Power
  • 
  • 
  • $\eta < 0$ で risk-averse, $\eta > 0$ で risk-seeking
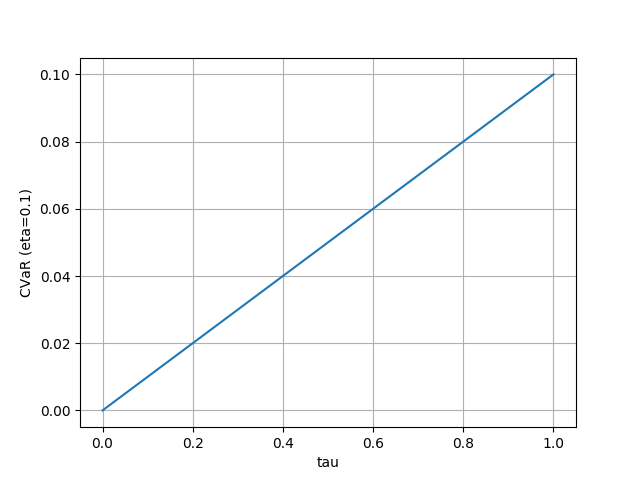
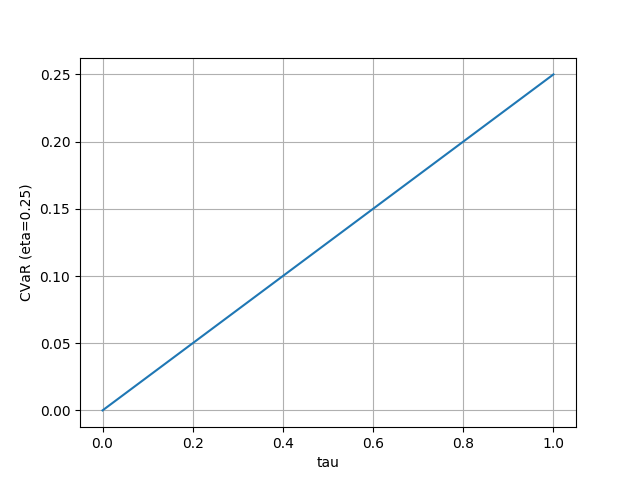
• Conditional value-at-risk
  • 
  • ⁴

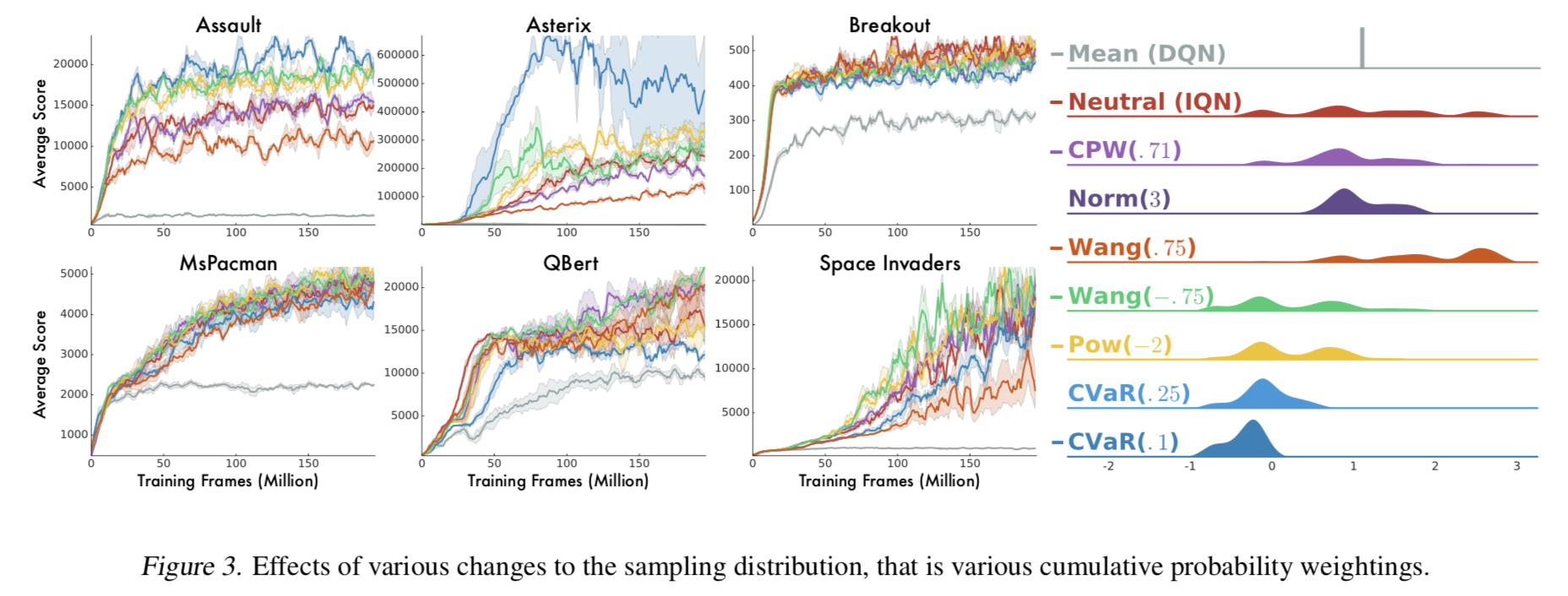
• Fig. 3 右から、 $\tau$ の分布を歪ませると価値分布もそれに合わせて歪んでいることが分かる
  • Norm(3) と CPW(.71) は分布の裾を小さくしている
  • Wang と CVaR は risk-averse/risk-seeking の設定に合わせて分布が移動している
  • CVaR は $\tau > \eta$ の点のサンプル確率がゼロになるので、分布の大きい側の裾がゼロになっている
• Fig. 3 左から、確かに risk distortion の効果が見られることがわかる
  • しかしゲームによって効果はまちまち
  • risk-averse は性能があがり、risk-seeking は性能が落ちる傾向があるが、理由はわからない

Atari-57 の実験結果

• ここでは IQN は risk-neutral、つまり $\beta$ を歪ませない設定

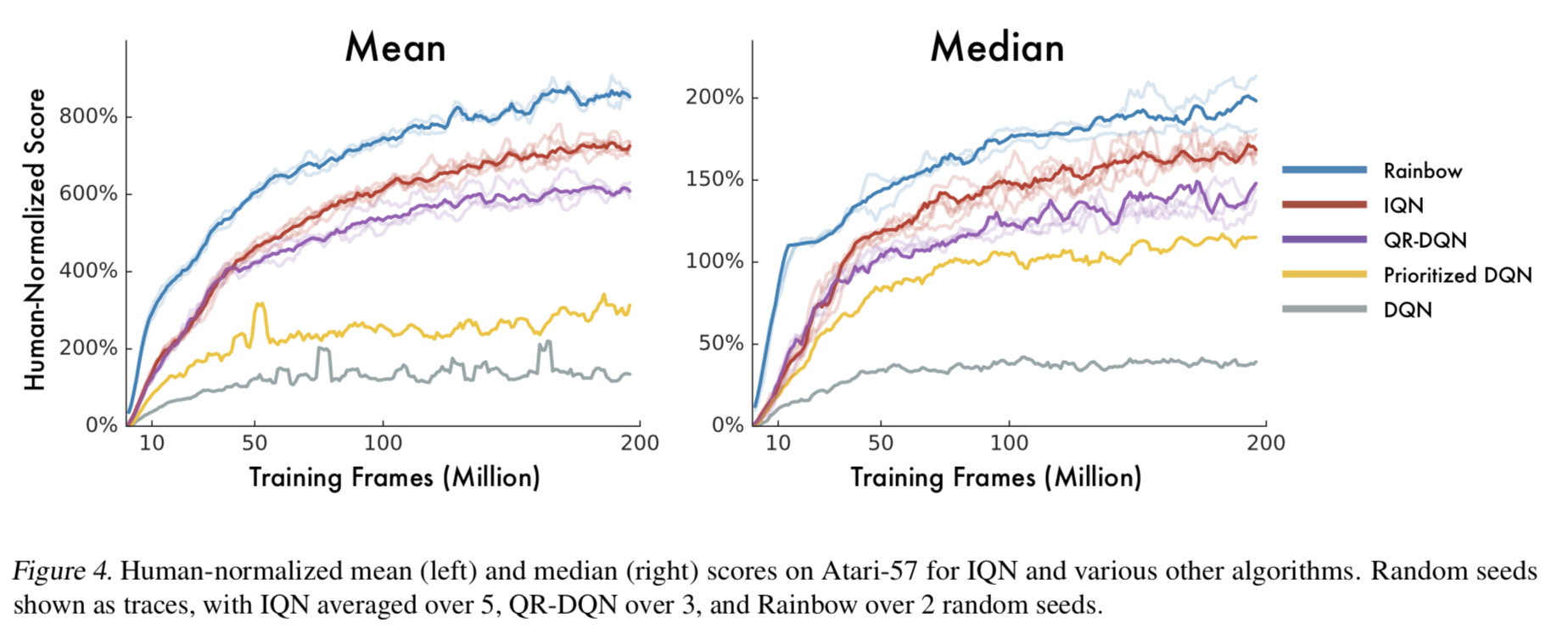
• Fig.4 から、IQN は同じように価値分布を活用している QR-DQN より良いことがわかる

• Tab.1 の Human Gap では IQN が Rainbow を上回っている。つまり、Rainbow が IQN よりも mean/median の意味で性能が良いのは、すでに人間の性能を超えているゲームでの差からきていることがわかる

議論と結論

• IQN は分布型の強化学習で、分布の形などの parameterization の事前の仮定に依存しない初めての手法である
• IQN は Rainbow と QR-DQN の差を半分に詰めた
• 理論的な解析が課題として残されている
  • QR-based アルゴリズムにも収束の保証があるだろうか？
  • Dabney et al (2018) の成果を拡張して、この論文を一般化したクラスにできるだろうか？
  • 歪んだ分布で探索をしたときの Bellman 作用素は不動点に収束するだろうか？
• IQN を連続行動タスクに適用することは promissing だ

参考資料

• [1806.06923] Implicit Quantile Networks for Distributional Reinforcement Learning
• [1707.06887] A Distributional Perspective on Reinforcement Learning
• [1710.10044] Distributional Reinforcement Learning with Quantile Regression
• [DL輪読会]DISTRIBUTIONAL POLICY GRADIENTS
• A Distributional Perspective on Reinforcement Learning · Issue #368 · arXivTimes/arXivTimes
• [1802.08163] An Analysis of Categorical Distributional Reinforcement Learning

感想

• Human Gap は IQN が Rainbow を上回る指標が見栄え的にほしいという意図があるのではと邪推してしまう

---

1. 恥ずかしながら QR-DQN の元論文を読んだことがないのですが、解説資料などではよく「(ヒストグラムのような離散的な近似ではなく) 分位点がどのくらいの値なのかを回帰で予測する」ような方法である、と見ます ↩

2. $\pi_\beta$ は (1) 式で定義されているとおりQ関数の値が必要となるが、価値関数を分布として扱っているため Q関数を求める際に積分が必要 (この記事の (1) 式の上の式の定義) となってしまうので、その積分を K 個のサンプルでの平均で代用しましょう の意 ↩

3. f の式を見るに、 $j = 1, \dots , d$ と思われる  ↩

4. これ累積分布関数にはなってない。本文中で 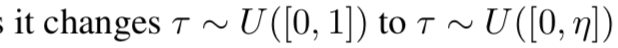と言っているので、たぶん本当は CVaR は累積分布関数の逆関数か？ ↩