幅優先探索の初歩【競技プログラミング】

はじめに

グラフ理論でいくつか投稿してきたけど、これまで「幅優先探索」については書いていなかったから、書いてみようと思う。

幅優先探索と深さ優先探索

• 幅優先探索について触れるなら、当然、深さ優先探索とセットで考えた方が良い。
• 実はこれまで、深さ優先探索を使ったアルゴリズムは何度も書いてきた。この2つのアルゴリズムは、頂点Aから頂点Bに移動した後の行動に違いが出る。
  • 深さ優先探索の場合
    • 移動先である頂点Bの先に、移動可能な頂点Cがあれば、頂点Cに進む
    • つまり、①A⇒B、②B⇒C
  • 幅優先探索の場合
    • 移動元である頂点Aから見て、頂点B以外の移動可能な頂点Dがあれば、頂点Dに進む
    • つまり、①A⇒B、②A⇒D
• さらに言えば、幅優先探索の場合、まず、スタート地点から、１回の移動で到達可能な全ての頂点に行き尽くした後、次は２回の移動で到達可能な全ての頂点に行き尽くし、その後、３回の移動で到達可能な全ての頂点に行き尽くす、....という流れとなる。
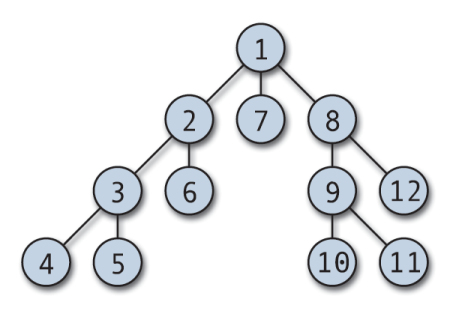
• グラフ理論だけの話でなく、木構造でも使われる用語だけど、木構造で言えば下図のような感じ。木構造もグラフ理論に含まれる木(連結かつ閉路無し)だから例としては良いよね。
  • 幅優先の探索順序
    
  • 深さ優先の探索順序
    
• このような、幅優先探索と深さ優先探索の使い分けは、実は簡単に実装できる。頂点番号を「深さ優先」の上図の番号を使うこととすると、上記グラフは次のように表現できる。

12 11 // 頂点数12、辺の数11
1 2 // 辺① 頂点1⇒頂点2
2 3
3 4
3 5
2 6
1 7
1 8
8 9
9 10
9 11
8 12

-　上記入力に対し、探索する頂点順に頂点番号を表示するコードは、次の通り

//グラフセット（有指向辺）頂点番号1減済み
let (N,M) = [readLine()!.split(separator:" ").map{Int($0)!}].map{($0[0],$0[1])}[0]
var gs = [[Int]](repeating:[],count:N)
for _ in 0..<M {
    let (a,b) = [readLine()!.split(separator:" ").map{Int($0)!}].map{($0[0]-1,$0[1]-1)}[0]
    gs[a] += [b]
    // gs[b] += [a] // 有指向のためコメントアウト
}

var que:[Int] = [] // 次に探索する場所をストックする配列

que.append(0) // 頂点1（インデックス表示:0）を始点とする

while !que.isEmpty {
    let q = que.removeLast() // -- 深さ優先探索のキモ
    
    // 頂点qに対する何かの作業をする
    print(q + 1 , terminator:" ") // 頂点番号を表示(インデックス表示+1)
    
    // 次の探索範囲を登録
    for g in gs[q] {
        que.append(g)
    }

}

• 上記コードの出力は、下記の通りであり、元の図では、左側から埋めていったのが、右側から埋めている違いはあるが、深さ優先探索となっているのが分かる。

1 8 12 9 11 10 7 2 6 3 5 4 

• 次に、上記コードの一カ所だけ変えて、幅優先探索を実装する。変化させるのは、removeLast()⇒removeFirst()のみであり、変更後の出力は以下のとおりで、幅優先探索となっていることが分かる。

1 2 7 8 3 6 9 12 4 5 10 11 

• 次に探索する場所を配列queにため込むのは両者とも同じだけど、その配列から取り出す際、お尻から取り出す(removeLast)か、頭から取り出す(removeFirst())かが違う。
• ちなみに、お尻から取り出すデータ構造を「スタック」と呼び、あたまから取り出すデータ構造を「キュー」と呼びます。

幅優先探索での最短距離測定

• 幅優先探索は、上図の通り、始点から一番近い点から探査していくので、辺の重みが全て「1」であれば、ある点Aからある点Bまでの距離を調べるコードは単純な形で書ける。
• 例えば、下のグラフについて考える。
  
• 上のグラフは、次のように表現できる。

9 12 // 頂点の数:9個、辺の数:12本
1 3 // 辺① 点1-点3 _ 全て無指向辺とする
3 9
9 8
8 2
2 1
2 4
4 3
4 6
6 9
9 5
5 7
7 6

• スタートを頂点①として、各頂点までの距離を求めるコードは、次の通り

//グラフセット（無指向辺）頂点番号1減済み
let (N,M) = [readLine()!.split(separator:" ").map{Int($0)!}].map{($0[0],$0[1])}[0]
var gs = [[Int]](repeating:[],count:N)
for _ in 0..<M {
    let (a,b) = [readLine()!.split(separator:" ").map{Int($0)!}].map{($0[0]-1,$0[1]-1)}[0]
    gs[a] += [b]
    gs[b] += [a] // 無指向のため追加
}

var que:[Int] = [] // 次に探索する場所をストックする配列
var d = [Int](repeating:-1,count:N) // 頂点までの距離を格納

let start = 1 // スタートの頂点 

let s = start - 1 // インデックス表示に合わせるため、-1する

que.append(s) // 頂点1（インデックス表示:0）を始点とする
d[s] = 0 // 頂点1までの距離を0とする

while !que.isEmpty {
    let q = que.removeFirst() // .. 幅優先探索のキモ！(※)
    
    // 次の探索範囲を登録
    for g in gs[q] {
        if d[g] != -1 {continue}
        que.append(g)
        d[g] = d[q] + 1 // 次の点は距離が1増える
    }
}

print(d) // [0, 1, 1, 2, 3, 3, 4, 2, 2]： 各頂点までの距離
print(d[5-1]) // 3：頂点5までの距離

• 上記コードを実行すると、求める解となった。
• 上記の 幅優先探索のキモ！(※)と書かれた部分を、removeFirst()からremoveLast()に変えて、深さ優先探索にするとどうなるか？
• removeLast()に変えると、配列dは[0, 1, 1, 2, 5, 3, 4, 2, 4]となり結果が変わり、頂点5までの距離も、3から5に変わっている。当然、本来は3が正解。5となったのは、深さ優先探索により、おそらく、1-3-9-6-7-5と進んだからと思われる。
• 今回、辺の重みのない場合の最短経路を幅優先探索で求めたが、辺に重みがあるときは少し面倒で、ダイクストラ法を使う必要がある。

コンテスト問題での活用例

• ABC088のd問題は、上記で説明したような見た目の丸と線でつくられたグラフじゃなく、将棋盤のようなマスの形をしている。とはいえ、上下左右の移動を辺、各マスを頂点と考えれば、辺の重みのないグラフと同等である。
• 上記コンテスト問題は、以下の通り。
  • 将棋盤もどきは、縦H×横Wのマスで構成され、各マスは黒と白のどちらかとなっており、白のマスのみが通行可能となっている。
  • 座標:(x軸,y軸)の（1,1）をスタート、(W,H)をゴールとし、経路を残しながら白のマスを黒く塗ることとした場合、黒く塗れるマスは最大何マスか？
  • これはつまり、スタートとゴールの最短経路の長さを求める問題と変わらない。
  • 解答（黒く塗れるマスの数）は、「最初の白マス総数 - (最短経路の長さ ＋ 1)」となる。
  • 最後の「＋1」とは「スタートのマス」が経路の長さに含まれないための調整である。
• 入力例は下記の通り

10 37 // 縦10マス×横37マス
.....................................
...#...####...####..###...###...###.. // 「.」が白マス、「#」が黒マスを示す。
..#.#..#...#.##....#...#.#...#.#...#.
..#.#..#...#.#.....#...#.#...#.#...#.
.#...#.#..##.#.....#...#.#.###.#.###.
.#####.####..#.....#...#..##....##...
.#...#.#...#.#.....#...#.#...#.#...#.
.#...#.#...#.##....#...#.#...#.#...#.
.#...#.####...####..###...###...###..
.....................................

• これを解くコードは以下の通り

//タプル格納 整数
let (H,W) = [readLine()!.split(separator:" ").map{Int($0)!}].map{($0[0],$0[1])}[0]

// 配列イニシャライズ用のextension -- (※)
extension Array {
    init(_ size: Int, _ value: Element) {
        self = [Element](repeating: value, count: size)
    }
}

/// サイズ(H+2)×(W+2)の配列Sに入力の二次元マップを格納する
/// 元の二次元マップの上下左右を黒マスで埋めることにより、道(白マス)の周りに必ず壁(黒マス)が存在するようにしている。
/// これにより、スタート地点､ゴール地点の配列でのインデックス表示の座標も(1,1)(W,H)になる事となった。
let wall = [Character](W+2,"#") // エクステンション(※)活用
var S:[[Character]] = []
S.append(wall)
for _ in 0..<H {
let vs = Array("#" + readLine()! + "#")
    S.append(vs)
}
S.append(wall)

// 座標(1,1)から座標(x,y)までの最短距離を格納する配列ds
var ds = [[Int]](H+2,[Int](W+2,-1)) // エクステンション(※)活用

// 上下左右の移動内容を配列登録
let dirs:[(Int,Int)] = [(1,0),(0,1),(-1,0),(0,-1)]

// 幅優先探索するキュー配列
var qs:[(Int,Int)] = [] // i,j

// スタート地点の距離は本来は0だが、最後にスタート地点のマスの面積調整があるので、予め1としておく
ds[1][1] = 1

qs.append((1,1)) // スタート地点をキューに登録

while !qs.isEmpty {
    let (i,j) = qs.removeFirst() // 幅優先探索探索！！！
    if (i,j) == (H,W) {break} // ゴールなら終了
    for (ud,lr) in dirs {
        // 移動先座標
        let (di,dj) = (i + ud , j + lr)

        // 移動先のチェック
        if S[di][dj] == "#" {continue} // 壁(黒マス)ならスキップ
        if ds[di][dj] != -1 {continue} // 到達済みならスキップ

        // 移動先に対する処理
        ds[di][dj] = ds[i][j] + 1 // 距離を登録
        qs.append((di,dj)) // キュー配列に追加
    }
}

// 白マス(道路)のマスの数
let load = S.flatMap{$0}.filter{$0 == "."}.count

print(ds[H][W] == -1 ? -1 : load - ds[H][W]) // ds[H][W]==-1は、ゴール不可ということ

• 上記コードは特に説明しないけど、コメントを色々書いているから分かるよね。

おわりに

• 今回、初歩と言うことで幅優先探索を紹介したけど、将来、上級の幅優先探索を紹介するかは未定です。
• そもそも、幅優先探索の奥深さについて、現時点では良く理解してないから、初歩と言って誤魔化しただけだらからね。
• まぁ、続きは「乞うご期待」ってことで。