はじめに
この記事では、ADALINEやバッチ勾配降下法、確率的勾配降下法、データの標準化について説明したあと実際にPythonを使い「一対多(OvR)」の手法を用いて少し発展的な多クラス分類をやってみようと思います。
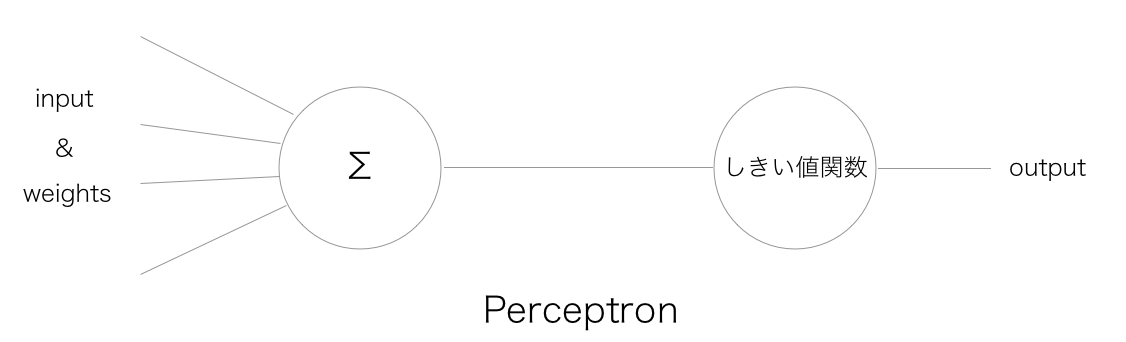
ADALINEはパーセプトロンとの比較で語られることが多いので、パーセプトロンについては以下の記事を参考にしてください!
人工ニューロンとパーセプトロン【機械学習再勉強】
まずADALINEとは何かからやっていきます
理論的背景
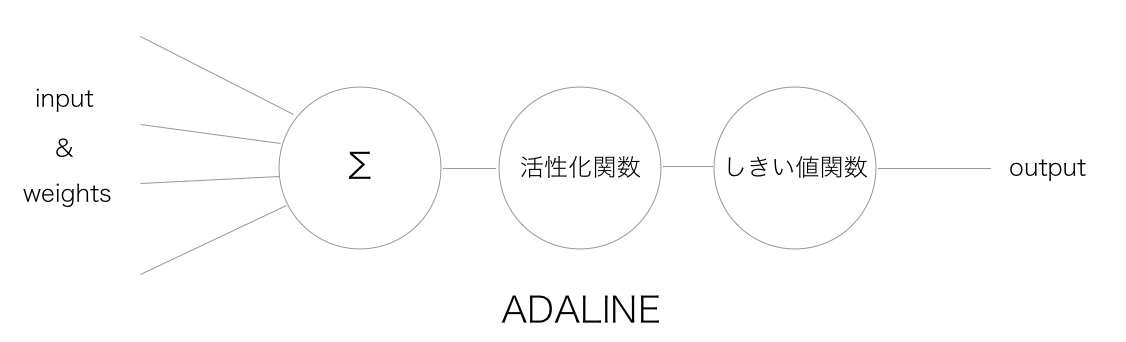
ADALINE
Adaptive Linear Neuronの略で、直訳すると「適応する能力のある線形ニューロン」といったところでしょうか。
パーセプトロンの数年後に発表されたパーセプトロンの改良版といえるものです。
初めて活性化関数、コスト関数の概念を持ち込んだものになります。
次の動画を見ると読み方はアダラインでいいっぽい。
最初にでた1960年の初期のWidrowさんの論文(AN ADAPTIVE "ADALINE" NEURON USING CHEMICAL "MEMISTORS")を見ると
The latter procedure is quite simple to implement, and can be analyzed by statistical methods that have already been developed for the analysis of adaptive sampled data systems.
"後者の手順(ADALINE)はとてもシンプルに実行でき、すでにadaptive sampled data systemsの分析のために開発されている統計的な分析手法を用いて分析することができる"
とあり、統計学の最適化手法に新しい発想を見てとれます。
以下が概念図のパーセプトロンとの比較図です。
これが現在のようなパソコンがなかった頃の原初のADALINEです。
簡単な論理回路の組み合わせでできていることがわかります。
無料でネットに公開されているので引用させていただきます。

バッチ勾配降下法
ADALINEではコスト関数として誤差平方和を定義し、このコスト関数を最小にするように重みの更新を行っていきます。
$$
J({\bf w}) = \frac{1}{2}\sum_{i}(y^{(i)} - \Phi(z^{(i)}))^2
$$
ここで、$y^{(i)}$はi番目の真のクラスラベルを、$\Phi$は活性化関数を、$z^{(i)}$はi番目のインプットである$x^{(i)}$と重み${\bf w}$のドット積を表しています。
頭に1/2をつけたのは、微分したときに打ち消されるようにで本質的な意味はありません。(スケールが変わるだけで、最小をとる${\bf w}$は変わらないが計算が簡単になる)
ここからは少し数学的な話になりますが、頑張ってついてきてくれると嬉しいです。
一回のイテレーションでの重みの変化$\Delta {\bf w}$は負の勾配に学習率$\eta$をかけたものをして定義します。
$$
\Delta {\bf w} = -\eta \nabla J({\bf w})
$$
負の勾配とはイメージとしては、3次元空間の場合だと坂の一番急斜面の方向ベクトルです。
ここでこれを計算すると各次元について、
$$
\begin{align}
\frac{\partial J}{\partial w_j}&=\frac{\partial}{\partial w_j}\frac{1}{2}\sum_i(y^{(i)} - \Phi(z^{(i)}))^2 \\
&= \frac{1}{2}\sum_i2(y^{(i)} - \Phi(z^{(i)}))\frac{\partial}{\partial w_j}(y^{(i)} - \sum_k(w_k x_k^{(i)})) \\
&=-\sum_i(y^{(i)} - \Phi(z^{(i)}))x_j^{(i)}
\end{align}
$$
のような形になります。ここの計算は、わからなかったらまあこういうものだと思ってください。
パーセプトロンの場合は、
$$
\Delta w_j = \eta(y^{(i)} - \hat{y}^{(i)})x_j^{(i)}
$$
だったので、似ていますね。
バッチ勾配降下法は、上の式で$\Sigma$がついていることからわかるようにトレーニングセットのすべてのサンプルに基づいて計算されます。
これらの数式をオブジェクト指向のアプローチに基づき実際に実装してみましょう。
まず、numpyをインポート
import numpy as np
そしてクラスを定義します。
class AdalineGD:
pass
GDとは勾配降下法(gradient descent)の略です。
次に各メソッドを定義していきます。
まずはコンストラクタから、
def __init__(self, eta=0.01, n_iter=50):
self.eta = eta
self.n_iter = n_iter
etaは学習率、n_iterはエポック数。
次に、重みを初期化しましょう。ごく小さな正規分布で初期化します。
def init_weight(self, X):
self.w_ = np.random.normal(0, 0.01, size=X.shape[1] + 1)
次に総入力(net input)用のメソッドです。
def net_input(self, X):
return np.dot(X, self.w_[1:]) + self.w_[0]
あと必要なものは活性化関数メソッド、予測メソッド、トレーニング用メソッドなので一気に書いていきます。
# 活性化関数
def activation(self, X):
return X
# 予測
def predict(self, X):
return np.where(self.activation(self.net_input(X)) >= 0.0, 1, -1)
# トレーニング
def train(self, X, y):
self.init_weight(X)
self.cost_ = [] # 性能評価のため取っておく
for i in range(self.n_iter):
net_input = self.net_input(X)
output = self.activation(net_input)
errors = y - output
# 重みの更新
self.w_[1:] += self.eta * X.T.dot(errors)
self.w_[0] += self.eta * errors.sum()
# コスト関数の計算
cost = (errors**2).sum() / 2.0
self.cost_.append(cost)
return self
以上まとめて書くと、
class AdalineGD:
def __init__(self, eta=0.01, n_iter=50):
self.eta = eta
self.n_iter = n_iter
def init_weight(self, X):
self.w_ = np.random.normal(0.0, 0.01, size=X.shape[1] + 1)
def net_input(self, X):
return np.dot(X, self.w_[1:]) + self.w_[0]
def activation(self, X):
return X
def predict(self, X):
return np.where(self.activation(self.net_input(X)) >= 0.0, 1, -1)
def train(self, X, y):
self.init_weight(X)
self.cost_ = []
for i in range(self.n_iter):
net_input = self.net_input(X)
output = self.activation(net_input)
errors = y - output
# 重みに更新
self.w_[1:] += self.eta * X.T.dot(errors)
self.w_[0] += self.eta * errors.sum()
# コスト関数の計算
cost = (errors**2).sum() / 2.0
self.cost_.append(cost)
return self
となります。
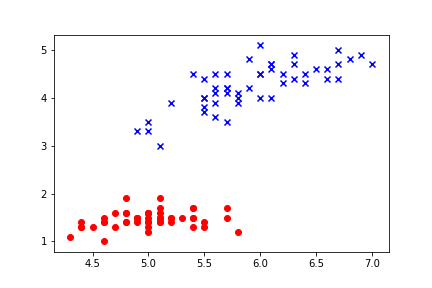
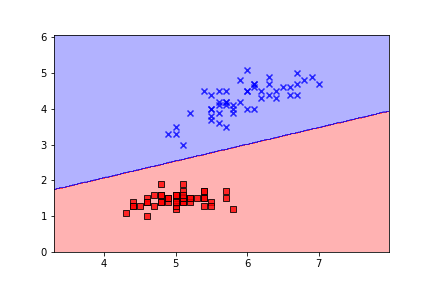
実際にこれを用いて、2値分類を行ってみます。
ada = AdalineGD(0.0001, 100)
学習率を0.0001にして100回イテレーションを回します。
これでトレーニングを行うと、以下のようにうまく分類されました。
特徴量の標準化
これはスケーリングの手法の一種である。
例えば、j番目の特徴量を標準化するには、サンプルの平均$\mu_j$をすべてのトレーニングサンプルから引いて、標準偏差$\sigma_j$で割ればいい。
$$
x_j^{'} = \frac{x_j - \mu_j}{\sigma_j}
$$
この標準化を施すことにより、各特徴量での収束スピードが均等になり結果として全体として早く収束するようになります。
ちなみにNumpyのmeanメソッドとstdメソッドを用いることでこの標準化は簡単に実現できます!
確率的勾配降下法
これはSGD(stochastic gradient descent)ともよく言う。
バッチ勾配降下法と異なり、トレーニングサンプルごとに段階的に重みを更新する。
$$
\eta(y^{(i)} - \Phi(z^{(i)})){\bf x}^{(i)}
$$
この手法はオンライン学習に使えるというメリットがあります。
オンライン学習については以下を参照してみてください。
ADALINEで3値分類してみる
ここからが今回の本題です。
一対多分類器
i=1,…,k−1の各クラス i それぞれについて,クラス i なら 1を,その他のクラスなら 0 を識別する2値分類器を学習する. クラス k については,k−1個の分類器が全て 0 を出力すれば,クラスkと分かる.
つまり、N値分類を行うためには分類器がN個必要ということになる。
まずデータを用意する。
var = 0.1 # 分散
count_of_data = 50 # データ数
# 二次元正規分布を3つ作る
points_ax = np.random.normal(3, var, [count_of_data])
points_ay = np.random.normal(3, var, [count_of_data])
points_bx = np.random.normal(1, var, [count_of_data])
points_by = np.random.normal(3, var, [count_of_data])
points_cx = np.random.normal(2, var, [count_of_data])
points_cy = np.random.normal(5, var, [count_of_data])
x = np.hstack((points_ax, points_bx, points_cx))
y = np.hstack((points_ay, points_by, points_cy))
# 学習データとラベルを用意
datas = np.array([x, y]).T
labels1 = np.hstack((np.ones(count_of_data), np.zeros(count_of_data) - 1, np.zeros(count_of_data) - 1))
labels2 = np.hstack((np.zeros(count_of_data) - 1, np.ones(count_of_data), np.zeros(count_of_data) - 1))
labels3 = np.hstack((np.zeros(count_of_data) - 1, np.zeros(count_of_data) - 1, np.ones(count_of_data)))
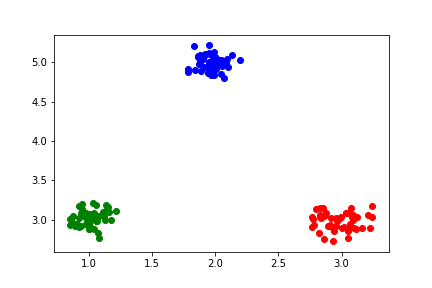
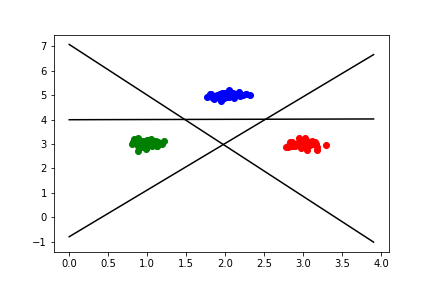
# 図示
plt.scatter(points_ax, points_ay, c='red')
plt.scatter(points_bx, points_by, c='green')
plt.scatter(points_cx, points_cy, c='blue')
plt.show()
ここから学習させていく。
# 3値分類なので学習器を3つ用意
ada1 = AdalineGD(0.0001, 3000)
ada2 = AdalineGD(0.0001, 3000)
ada3 = AdalineGD(0.0001, 3000)
# トレーニング
ada1.train(datas, labels1)
ada2.train(datas, labels2)
ada3.train(datas, labels3)
あとは決定境界を3本引いて見て、ちゃんと分類されているかどうか確認してみる。
# 重みの抽出
w1 = ada1.w_
w2 = ada2.w_
w3 = ada3.w_
# 図示
plt.scatter(points_ax, points_ay, c='red')
plt.scatter(points_bx, points_by, c='green')
plt.scatter(points_cx, points_cy, c='blue')
plt.plot(x0, -w1[1] * x0 / w1[2] - w1[0] / w1[2], c='black')
plt.plot(x0, -w2[1] * x0 / w2[2] - w2[0] / w2[2], c='black')
plt.plot(x0, -w3[1] * x0 / w3[2] - w3[0] / w3[2], c='black')
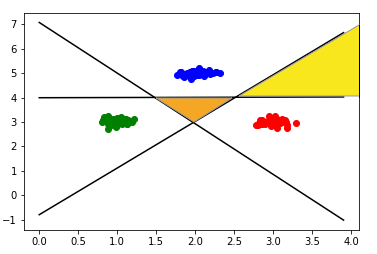
図を見ると、平面が7つの領域に分割されているが、この領域はそれぞれ意味を持つ。
例えば下図の真ん中のオレンジの領域は赤、青、緑どれか全く不明であることを意味し、下図黄色の領域は緑ではない(が赤か青かどちらかはわからない)と判断された領域だといえると思われる。
おわりに
今回はパーセプトロン、ADALINEから始まりバッチ勾配降下法、特徴量のスケーリング、確率的勾配降下法について見て最後にADALINEによる3値分類までやってみました。
まだまだ試行錯誤しつつなので、間違いやアドバイスなどあればなんでも教えてくださいー!