はじめに
わりとがっつり機械学習をちゃんとやっていきたいと思いました。そこで後輩と一緒に今一度、「なんとなくできる」じゃなくてしっかりと理解していけるように勉強しようと思いました。
一緒に本を読んで行ってそこで感じたことをまとめていけるとなと思いました。
僕自身、統計学には片足を突っ込んではいるんですが、機械学習はイマイチなのでなにかあればご指摘いただけますと幸いです。
学習には
[第2版]Python 機械学習プログラミング 達人データサイエンティストによる理論と実践
ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
を使っています。
とても良い本なので気になりましたら是非買ってみるといいかもです!(ステマではありません!)
ニューロンについて
生物学でやったあれです。僕は専攻が分子生態学で専門分野ではないですが、ニューロンとは神経細胞のことで、樹状の突起から刺激を受け、軸索から他のニューロンに刺激を伝達します。
ちょっと絵心なくて申し訳ないです。
が、こんな感じです。なんでこんな話になるかというと、脳はニューロンの集まりで、外界で受けた刺激を多数のニューロンで処理した結果が僕ら人間のアウトプットになっており、このメカニズムを表現したのが人工ニューロンであるためです。
例えば、絵を見てガンダムを認識する問題では
- 1:絵を見る
- 2:ツノはあるか?MS(モビルスーツっぽいか)?ロボットっぽいか?
- 3:これガンダムかそうでないかと思う。
というプロセスを辿ります。ここでいうと目で見た刺激は1、思考は2、アウトプットは3といった具合です。
つまり、僕らがものを見て、どう思うかといった処理は目などの受容器官とニューロンによって成り立っているということです。
人工ニューロンについて
上記で、いかにして生物が状況を判断しているかということを書きました。そしてこのプロセスを人工ニューロンとして定義すると、
output = function(z);\\
z = \sum_{i=1}^{n} x_iw_i;
functionの部分は処理結果をどうするかといったところでここはパーセプトロンモデルを説明する上で非常に重要なんですが、一旦はニューロンの説明ということであとで説明します。
ということになります。ここでいう${x_i}$はインプット、${w_i}$はそれに対応する重み付けです。
例えば、安直にたったひとつのニューロンでとある人物を可愛いかそうでないか判断しているとします。またこの際に、zの値が0.5以上であれば可愛い(1)、0.5未満であれば可愛くない(-1)と判断しているとします。するとこの事象は、
output = function(z) = \left\{
\begin{array}{ll}
1 & (z \geq 0.5) \\
-1 & (z \lt 0.5)
\end{array}
\right.
といった感じになります。また、この時に僕は可愛いと思うんだけど、僕の親友は可愛くないというといったケースではインプットになる${x_i}$は一緒なんですが、その重み付け${w_i}$が僕と親友とでは違うためこのような結果の際がひき起こされています。現実世界でいうところの、性格を重視したり、趣味を重視したりといった重みが違うといった感じですね。
実際の計算で使われる行列
計算では行列行います。
数Cちゃんとやってない僕としてはちょっと再整理したいところなので、書くと、
\sum_{i=1}^{3} x_iw_i = w^T x =
\left(\begin{matrix}
w_1 \\ w_2 \\ w_3
\end{matrix} \right) \times (\begin{matrix}
x_1 & x_2 & x_3
\end{matrix}) = x_1w_1 + x_2w_2 + x_3w_3;
こんな感じになります。
パーセプトロンとは
パーセプトロンには大きな特徴があります。それは、閾値によってアウトプットが異なるという点です。ここについては先ほど紹介した、
output = function(z) = \left\{
\begin{array}{ll}
1 & (z \geq 0.5) \\
-1 & (z \lt 0.5)
\end{array}
\right.
という可愛いと思うか思わないか、そして人によって書くインプットの重みが違うよねという話です。
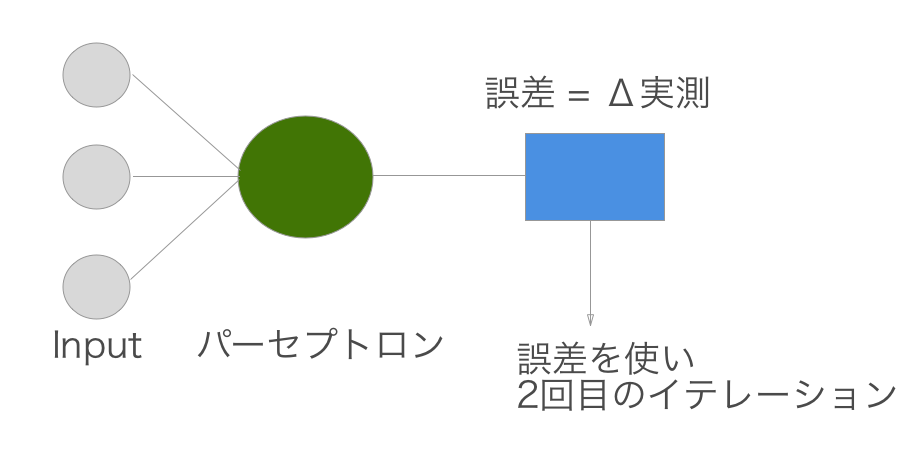
パーセプトロンの学習規則
いかようにしてパーセプトロンは学習をしていくのかというと、感覚値としては個人的には最小二乗法に近いんじゃないかなって思います。
まず下記のフローによって学習を行います。
Δは差分を意味します。
ここら辺の数学に突如出てくる系の文字の意味と読みわかんなくなるので気になった方はこちらをご覧ください。
ギリシャ文字
あと、これも統計あるあるなんですが、
\hat{y}
\bar{u}
とか、出てきたりします。が、基本的にこういう時にこの記号を付与するみたいなルールがあって覚えておくと理解が捗るかもしれないです。
数式記号の読み方・表し方
話が逸れましたが、つまりどういうことかというと、学習では何回かイテレーションを回して学習をさせます。その時に一回実行して、与えられたデータとの誤差を算出し、それを元に重みを更新する。ということを繰り返させると最終的に重みは収束し、予測モデルが完成するという寸法なのです。
ハイパーパラメータの設定
さぁイテレーションを回すぞ!といったところなんですが、残念なことに最初に計算させようにも最初の段階では重みがわからないのです。そこで基本的には0あるいは微小な値の乱数を設定することによって第一回目の値を補います。これをハイパーパラメータといいます。こういった、こちら側から推定のために与える数値のことです。乱数は一様分布や正規分布などが使われることが多いですが、一体何を与えたらいいのか?ってなるとこういうところに職人芸的なものがあるみたいですね。
僕自身あんまり知見がないのでその点に関してはよくわからなかったので学生時代も一様分布やガンマ分布といった幅広なものを使っていた記憶があります。
重みの更新
これで1回目については${\hat{y}}$を出すことができました。
\hat{y} = w_j^T x
jはj番目のイテレーションを示します(1回目なので1なんですが${w_1}$という1番目のインプットに対する重みと混同しないようにしました)。
そして、この次に
w_{j+1} = w_j + η(y - \hat{y})x;
と2回目に用いる重みを更新します。ただ単に、
η(y - \hat{y})x
を現在の重みに加えるだけです。
さてここで出てきたη(読み:イータ)は学習率をさします。
学習率とは、これもこちら側で決める値になり、${0 \leq η \leqq 1}$です。
学習率も職人芸なのかもしれません・・・。
学習率が低いとどうなるのか?高いとどうなるのか?についてはとても良い記事があります!。僕でもわかりました!
TensorFlowを使って学習率による動きの違いを確認する
${y - \hat{y}}$については純粋に残差みたいなものです。実測値と予測値の差分になります。Xをかけている理由としては、${y - \hat{y}}$は一次元の値なのに対し(複数次元もありうる)、w,xはinputがあってそれに対応するwがそれぞれあるためxの値に応じた変化量を加算せるためです。
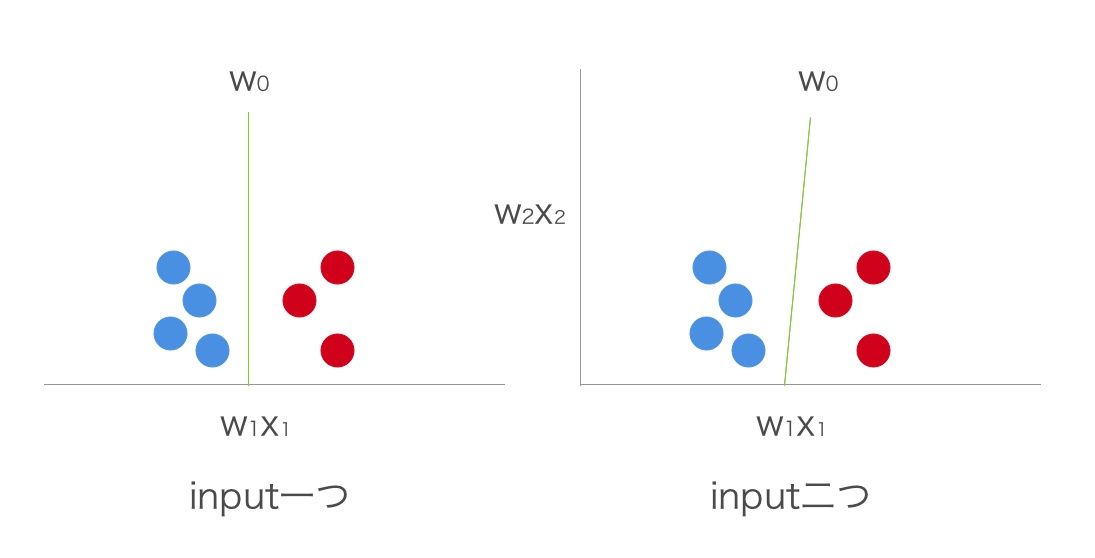
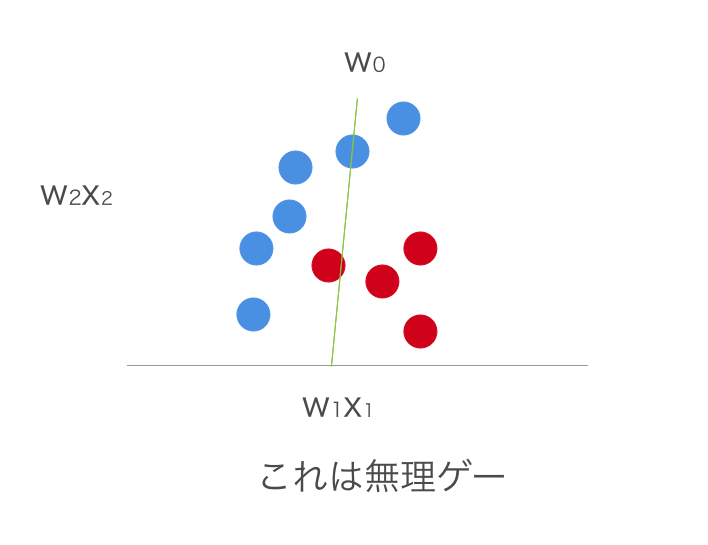
単層パーセプトロンの弱点
単層パーセプトロンは線形分離できないものに対しては無力です。
というのもなぜかというと、例えばinputが一つしかないモデルがあったとします。すると、
\hat{y} = x_1 w_1 = \left\{
\begin{array}{ll}
1 & (z \geq w_0) \\
-1 & (z \lt w_0)
\end{array}
\right.
w_0は閾値。
これは結局、特定の点${w_0}$で分離しているだけということになります。
仮にinputが二つになっても、
\hat{y} = x_1 w_1 + x_2 w_2= \left\{
\begin{array}{ll}
1 & (z \geq w_0) \\
-1 & (z \lt w_0)
\end{array}
\right.
特定の点から直線で分離しているという区分けが二つになるだけなので、結局線形分離しているにすぎません。これは${w_i x_i}$という単純な積であることと、閾値によって分けていることに起因します。
あんまり頭よろしくないので疑問に思いちょっと考えてみたら、
w_0 = w_1 x_1 + w_2 x_2; \\
w_2 x_2 = w_0 - w_1 x_1;
といった感じになってしまいます・・・。
実装
パーセプトロン
class Perceptron(object):
def __init__(self, eta = 0.01, iter = 100, seed_state = 1):
self.eta = eta;
self.iter = iter;
self.seed_state = seed_state;
def predict(self, x):
## 閾値をw0として定義。
allInput = np.dot(x, self.w_[1:] + self.w_[0]);
## 閾値判定
outPut = np.where(allInput >= 0.0, 1, -1);
return outPut;
# 最初の重みを生成
def generateWeight(self, size = 1):
rgen = np.random.RandomState(self.seed_state);
weights = rgen.normal(loc=0, scale=0.01, size=size);
return weights;
def train(self, x, y):
## 初期化
self.w_ = self.generateWeight(1 + x.shape[1]);
self.errors_ = [];
for _ in range(self.iter):
errors = 0;
for xi, target in zip(x,y):
update = self.eta * (target - self.predict(xi));
self.w_[1:] += update * xi;
self.w_[0] += update;
errors += int(update != 0.0);
self.errors_.append(errors);
return self;
初期化
def __init__(self, eta = 0.01, iter = 100, seed_state = 1):
self.eta = eta;
self.iter = iter;
self.seed_state = seed_state;
- eta:学習率
- iter:イテレーション回数
- seed:乱数発生のためのシード
と言ったところです。
重みの初期化
def generateWeight(self, size = 1):
rgen = np.random.RandomState(self.seed_state);
weights = rgen.normal(loc=0, scale=0.01, size=size);
return weights;
初期化で代入したseedを使って、正規分布に従う乱数を発生させます。この時、size分の乱数を発生させます。
予測式
def predict(self, x):
## 閾値をw0として定義。
allInput = np.dot(x, self.w_[1:] + self.w_[0]);
## 閾値判定
outPut = np.where(allInput >= 0.0, 1, -1);
return outPut;
予測式は、
output = function(z);\\
z = w^T x;
であり、functionは特定の閾値以上であれば1、そうでなければ-1を返すようになっていました。
つまり、閾値をαとすると、
z \geq α \rightarrow 1\\
z \lt α \rightarrow -1\\
となるので、
z - α \geq 0 \rightarrow 1\\
z - α \lt 0 \rightarrow -1
となります。そして、
x_0 = 1\\
w_0 = -α\\
z + {x_0}{w_0} = \sum_{i=1}^{n} x_iw_i + {x_0}{w_0} = \sum_{i=0}^{n} x_iw_i;
となります。これを体現するために、予測式は
allInput = np.dot(x, self.w_[1:] + self.w_[0]);
outPut = np.where(allInput >= 0.0, 1, -1);
内積をかけ、0以上なら1、0未満なら0を返す関数として実装しています。
訓練
def train(self, x, y):
## 初期化
self.w_ = self.generateWeight(1 + x.shape[1]);
self.errors_ = [];
for _ in range(self.iter):
errors = 0;
for xi, target in zip(x,y):
update = self.eta * (target - self.predict(xi));
self.w_[1:] += update * xi;
self.w_[0] += update;
errors += int(update != 0.0);
self.errors_.append(errors);
return self;
ここからが本題です。この関数は
- x:特徴量
- y:ラベル
を期待しています。
重み初期化
まず、重みの初期値を作成します。
self.w_ = self.generateWeight(1 + x.shape[1]);
self.errors_ = [];
この時、w.shape(1)は特徴量の数(n)なので、インプットの総数は${{w_0}{x_0}}$をたした、n+1になります。つまり、推定する重みの総数は${n + 1}$ということになります。
パーセプトロンでは、重みの更新式が
η(y - \hat{y})x
でした。ということは一致した場合は${y - \hat{y} = 0}$となり、その重みの更新が止まることになります(${w_0}$の更新によって変わるけど)。ですので、errors_は誤判断の数を記録させるためにあるだけで上記で今まで説明してきた数式とは関係がありませんので最後にうまくいったか確認用にあるだけという認識でいてください。
for _ in range(self.iter):
errors = 0;
イテレーションの回数分回します。この時にerrorsを初期化します。errors_にその時のイテレーションの誤差を記録させるためです。
for xi, target in zip(x,y):
update = self.eta * (target - self.predict(xi));
self.w_[1:] += update * xi;
self.w_[0] += update;
errors += int(update != 0.0);
self.errors_.append(errors);
最後に、errors_appendしてエラー数を記録させています。
このループはデータの総数分回すことになります。
データが100件あれば、100件分のデータを使って重みを更新して、1イテレーション終了となります。
update = self.eta * (target - self.predict(xi));
self.w_[1:] += update * xi;
self.w_[0] += update;
w_{j+1} = w_j + η(y - \hat{y})x;
を表しています。${{x_0}}$は1であるため、省略しています。
errors += int(update != 0.0);
最後に誤判定していた場合、errorsを1加算します。
実践
このパーセプトロンを使って分類してみましょう。
データの準備・前処理
import matplotlib.pyplot as plt;
import numpy as np;
# パラーメーター
typeAXMean = 2;
typeAYMean = 5;
typeBXMean = 3;
typeBYMean = 3;
_var = 0.1;
dataNumber = 50;
typeAX = np.random.normal(typeAXMean, _var, [dataNumber]);
typeAY = np.random.normal(typeAYMean, _var, [dataNumber]);
typeBX = np.random.normal(typeBXMean, _var, [dataNumber]);
typeBY = np.random.normal(typeBYMean, _var, [dataNumber]);
X_ = np.hstack((typeAX, typeBX));
Y_ = np.hstack((typeAY, typeBY));
labels = np.hstack((np.ones(dataNumber), np.zeros(dataNumber) -1))
variables = [];
for prop in zip(X_, Y_):
variables.append([prop[0], prop[1]])
variables = np.array(variables);
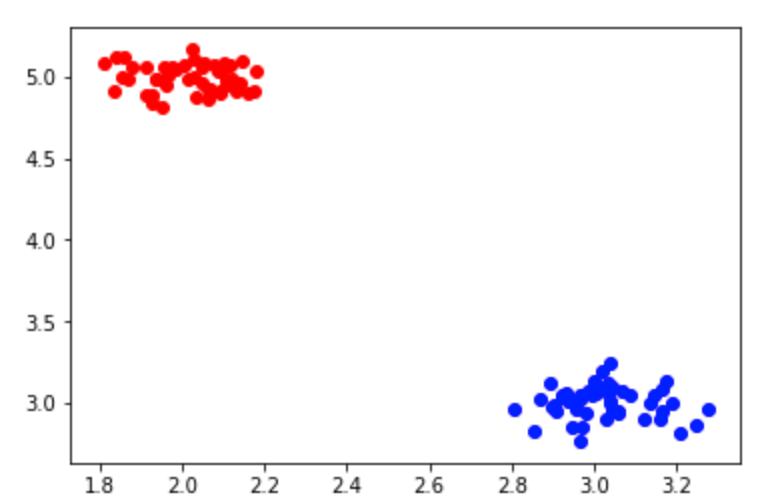
plt.scatter(typeAX, typeAY, color='red');
plt.scatter(typeBX, typeBY, color = 'blue');
plt.show();
以上によって、必要なデータを揃えました。
- variables:特徴量
- labels:ラベル
こんな感じなので楽勝で分類できそうです。
動かす
pers = Perceptron(eta = 0.01, iter = 10);
pers.train(variables, labels);
動かします。学習率は適当に設定しました。
plt.plot(range(1, len(pers.errors_) + 1), pers.errors_, marker='o');
plt.xlabel('iter');
plt.ylabel('errors');
plt.show()
誤判定の推移を見てみます。
plt.plot(range(1, len(pers.errors_) + 1), pers.errors_, marker='o');
plt.xlabel('iter');
plt.ylabel('errors');
plt.show()

こんな感じでうまくできていそうです。
終わりに
まだまだ勉強したてのひよっこなので、間違いや有益な情報ありましたらお教えください・・・!!