手動で単回帰分析をしてみようと思った -1-

はじめに

回帰分析の理論の理解を深めるために、回帰分析の強力な武器であるsklearnライブラリを用いずに手動で分析モデルを作ってみる。

回帰分析とは？

説明変数(入力データ)を用いて、目的変数(出力データ)の値を予測すること。今回は理論的に求めるため、簡単な説明変数1つの場合を考えてみる。(単回帰)

Pythonでの前準備

▼データを用意

import numpy as np
import pandas as pd
from pandas import DataFrame

data_age = np.array([20,20,28,38,33,34,22,37,
                     26,21,22,39,31,29,38,35,
                     32,27,30])

data_salary = np.array([410,500,480,710,630,600,430,
                        690,500,410,490,800,550,550,
                        700,700,650,540,600])

data = DataFrame({'年齢':data_age,
                  '所得':data_salary})

データの関係

上記のデータセットから以下のようなグラフを得ることができる。

このグラフから年齢と所得の関係を一次式で表してみることにする。(無理やり一次式に持っていくが、本当はもっと複雑な式になる。)

とりあえず予測される年齢をx、所得をyとおいて、y = ax + bと表すことを考える。
ここでデータが複数あることから単純にはaとbの値が決まらない事に注意する。最も妥当なaとbの値を算出するため、平均2乗誤差という考え方を用いる。
具体的には、y = ax + bを各データについて、予測(回帰)する所得yとの差を取って
y - 410= 20a + b - 410
y - 500= 20a + b - 500
y - 480= 28a + b - 480
...
と変形する。
この実データと予測データの値の差の2乗を、用意したデータ分(N個)だけ足し、その平均を取った値が平均2乗誤差Q(a,b)である。

Q(a,b) = \frac{1}{N}\sum_{k=0}^{n-1}(ax_k + b - y_k)

このy_kは実データとしての所得のことである。平均2乗誤差Q(a,b)が一番小さくなるようなa,bを求めることで年齢と所得の関係を一次式化してみることにする。

平均2乗誤差のグラフ

まず、Q(a,b)が一番小さくなるようなa,bを求めるためにaとbに様々な数値を入れて、平均2乗誤差の概形を書いてみる。

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import axes3d

# 任意のa,bを用意
a = np.linspace(-200,200,100)
b = np.linspace(-500,500,100)

# aとbの組み合わせが簡単に作れるよう
# それぞれを2次元配列に拡張(曲面を書くのに必要)
A,B = np.meshgrid(a,b)

# Qの計算用の関数
def calc_Q(x,y,a,b):
    result = (a * x + b - y)**2
    return np.mean(result)

# Q用の配列(0で初期化しておく)
Q = np.zeros([len(a),len(b)])

# a,bの全ての組み合わせでQを計算
for j in range(100):
    for k in range(100):
        Q[j,k] = calc_Q(data_age,data_salary,a[j],b[k])

# 3次元グラフの概形を書く
fig = plt.figure(figsize=[10,10])
ax = fig.add_subplot(111,projection="3d")
ax.view_init(45,10)
ax.set_xlabel("a",size=14,color="blue")
ax.set_ylabel("b",size=14,color="blue")
ax.set_zlabel("Q",size=14,color="blue")
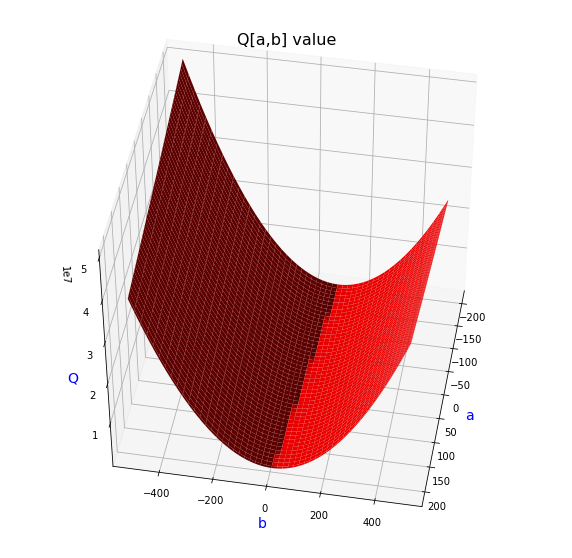
ax.plot_surface(A,B,Q,color="red")
plt.show()

グラフからa=50～200,b=0付近でQ[a,b]の値が最小になっている事が分かる。このグラフから恐らく極小値が一つであることが分かる。よって、再急降下法(傾きを利用した極小値の算出手法)を用いて、Q[a,b]の値が最小になるときのa,bの値を求めてみる。

続く。

参考

Python 数値計算入門
https://python.atelierkobato.com/mse/