pytorchでテンソル分解（CP分解）

はじめに

pytorchで行列分解の続き．

pytorchでテンソル分解（CP分解）をやる．
CP分解についてはUnderstanding the CANDECOMP/PARAFAC Tensor Decomposition, aka CP; with R codeを参照．良記事．

要は，ある３次元のテンソルXを，行列U, V, Wに分解する．

環境

• Python 3.6.1
• torch (0.2.0.post3)
• torchvision (0.1.9)

データの生成

どういうtoy dataを使うかは，さっきの記事をnumpyに直して使わせてもらった．

このプロットのような，X1, X2, X3を３３個ずつ準備して，それを重ねてる．
プロットのx軸については，ランダムな変動のみのX1と，50以下で定数（0.1）が足されているX2と，50以上で定数（0.1）が引かれいてるX3がある．
y軸については，ガウス分布の形をしている．つまり，真ん中ほど値が高くなっている．
これらを重ねるので，z軸についてはX1, X2, X3という３パターンが存在する．

make_toydata.py

from scipy.stats import norm
import numpy as np
import matplotlib.pyplot as plt
import torch
import make_toydata as toy

def plot_toy_dataset(toy_tensor, input_shape=None):
    """
    toy_tensor : torch.FloatTensor
    """
    if input_shape is None:
        l, m, n = (100, 100, 99)
    else:
        l, m, n = input_shape

    n_3 = int(n/3)
    toy_tensor = toy_tensor.numpy()
    X1 = toy_tensor[:,:,0:n_3]
    X2 = toy_tensor[:,:,n_3:2*n_3]
    X3 = toy_tensor[:,:,2*n_3:]
    fig = plt.figure()
    ax1 = fig.add_subplot(131)
    plt.imshow(X1[:,:,0])
    ax1.set_title("X1")
    ax2 = fig.add_subplot(132)
    plt.imshow(X2[:,:,0])
    ax2.set_title("X2")
    ax3 = fig.add_subplot(133)
    plt.imshow(X3[:,:,0])
    ax3.set_title("X3")
    fig.show()

def make_toy_dataset(input_shape=None):
    """
    input
        input_shape : tuple
        Ex. (l, m, n) = (100, 100, 99)
        n should be multiple of 3.
    output
        toy_tensor : torch.FloatTensor of size (l, m, n)
    """
    if input_shape is None:
        l, m, n = (100, 100, 99)
    else:
        l, m, n = input_shape
        
    n_3 = int(n/3)
    dom_norm = np.linspace(norm.ppf(0.01), norm.ppf(0.99), l)
    rv = norm()
    x = rv.pdf(dom_norm)
    X1 = np.tile(np.tile(x.reshape((l,1)), m).reshape((l,m,1)), n_3) + np.random.randn(l, m, n_3) * 0.25

    vec1 = np.zeros(m)
    vec1[0:int(m/2)] = 0.1
    vec2 = np.zeros(m)
    vec2[int(m/2):] = -0.1
    mat1 = np.dot(np.ones((l,m)), np.diag(vec1))
    mat2 = np.dot(np.ones((l,m)), np.diag(vec2))

    X2 = np.tile((np.tile(x.reshape((l,1)), m) + mat1).reshape((l,m,1)), n_3) + np.random.randn(l, m, n_3) * 0.1
    X3 = np.tile((np.tile(x.reshape((l,1)), m) + mat2).reshape((l,m,1)), n_3) + np.random.randn(l, m, n_3) * 0.1

    toy_tensor = np.concatenate((X1, X2, X3), axis=2).astype(np.float32)
    toy_tensor = torch.from_numpy(toy_tensor)
    return toy_tensor

plot関数の定義

学習したU, V, Wをプロットするための関数を定義する．

decomp_plot.py

import matplotlib.pyplot as plt
import torch
import numpy as np

def plot_U_V_W(model):
    U, V, W = get_U_V_W_numpy(model)
    fig = plt.figure()
    ax1 = fig.add_subplot(131)
    plt.imshow(U)
    ax1.set_title("U")
    ax2 = fig.add_subplot(132)
    plt.imshow(V)
    ax2.set_title("V")
    ax3 = fig.add_subplot(133)
    plt.imshow(W)
    ax3.set_title("W")
    fig.show()

def plot_rank1_U_V_W(model):
    U, V, W = get_U_V_W_numpy(model)
    fig = plt.figure()
    ax1 = fig.add_subplot(131)
    ax1.plot(U.flatten())
    ax1.set_title("U")
    ax2 = fig.add_subplot(132)
    ax2.plot(V.flatten())
    ax2.set_title("V")
    ax3 = fig.add_subplot(133)
    ax3.plot(W.flatten())
    ax3.set_title("W")
    fig.show()

def get_U_V_W_numpy(model):
    U = model.U.data.numpy()
    V = model.V.data.numpy()
    W = model.W.data.numpy()
    return U, V, W

def plot_means(X):
    if isinstance(X, torch.autograd.variable.Variable):
        X_num = X.data.numpy()
    elif isinstance(X, torch.FloatTensor):
        X_num = X.numpy()
    else:
        X_num = X

    mode1 = X_num.mean(2).mean(1)
    mode2 = X_num.mean(0).mean(0)
    mode3 = X_num.mean(0).mean(1)

    fig = plt.figure()
    ax1 = fig.add_subplot(131)
    ax1.plot(mode1)
    ax1.set_title("mode1 mean")
    ax2 = fig.add_subplot(132)
    ax2.plot(mode2)
    ax2.set_title("mode2 mean")
    ax2 = fig.add_subplot(133)
    ax2.plot(mode3)
    ax2.set_title("mode3 mean")
    fig.show()
    

テンソル分解

tensor_decomp.py

import torch
from torchvision import datasets, transforms
from torch.autograd import Variable
import torch.nn as nn
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt
import make_toydata as toy
import decomp_plot as dp

class Model(nn.Module):
    def __init__(self, input_shape, rank):
        """
        input_shape : tuple
        Ex. (3,28,28)
        """
        super(Model, self).__init__()

        l, m, n = input_shape
        self.input_shape = input_shape
        self.rank = rank

        self.U = torch.nn.Parameter(torch.randn(rank, l)/100., requires_grad=True)
        self.V = torch.nn.Parameter(torch.randn(rank, m)/100., requires_grad=True)
        self.W = torch.nn.Parameter(torch.randn(rank, n)/100., requires_grad=True)

    def forward_one_rank(self, u, v, w):
        """
        input
            u : torch.FloatTensor of size l
            v : torch.FloatTensor of size m
            w : torch.FloatTensor of size n
        output
            outputs : torch.FloatTensor of size lxmxn
        """
        l, m, n = self.input_shape
        UV = torch.ger(u, v)
        UV2 = UV.unsqueeze(2).repeat(1,1,n)
        W2 = w.unsqueeze(0).unsqueeze(1).repeat(l,m,1)
        outputs = UV2 * W2  
        return outputs

    def forward(self):
        l, m, n = self.input_shape
        output = self.forward_one_rank(self.U[0], self.V[0], self.W[0])

        for i in np.arange(1, self.rank):
            one_rank = self.forward_one_rank(self.U[i], self.V[i], self.W[i])
            output = output + one_rank
        return output


def my_mseloss(data, output):
    """
    input
        data : torch.autograd.variable.Variable
        output : torch.autograd.variable.Variable
    output
        mse_loss : torch.autograd.variable.Variable
    """
    mse_loss = (data - output).pow(2).sum()
    return mse_loss


###
# toy dataset
###

input_shape = (100, 100, 99)
X = toy.make_toy_dataset(input_shape)
toy.plot_toy_dataset(X, input_shape)


###
# train model
###

rank = 1
model = Model(input_shape, rank)
optimizer = optim.Adagrad(model.parameters(), lr=0.01, lr_decay=0, weight_decay=0)

X = Variable(X)

for batch_idx in np.arange(1000):
    optimizer.zero_grad()
    output = model.forward()
    loss_out = my_mseloss(X, output)
    loss_out.backward()
    optimizer.step()

    if batch_idx % 10 == 0:
        print(f'index : {batch_idx}, Loss: {loss_out.data[0]}')

X_hat = model()
dp.plot_rank1_U_V_W(model)

ちなみにSGDだと発散しやすかったので，Adagradを用いている．
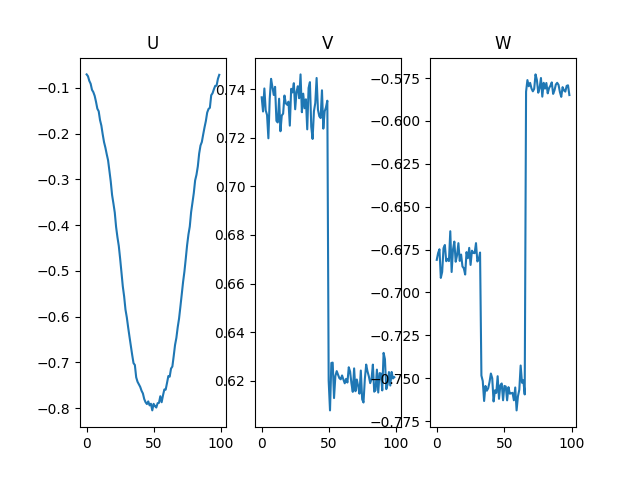
学習したU, V, Wはこんな感じ．

Uでy軸のガウス分布の成分を反映してる．
Vでx軸の定数の和による違いを２パターン反映してる．
WはX1, X2, X3の違い３パターンを反映してる．

前回の記事と同様に，各軸の平均と比べてみる．

UとWが負になっているが，どちらにせよ掛けたら正になっているのでその違いは無視すると，ほぼ一致している．

終わりに

• pytorchってforwardにfor文あっても良かったのか．

おまけ〜他の実装方法〜

最初，なぜかVとWが全く同じになり，なんでだろうなあと思っていくつか異なる実装方法で試した．
（結局，U, V, Wを返すところをU, V, Vを返していたという凡ミスだった...）
その副産物たちをおまけに乗っけておく．

class Model(nn.Module):
    def __init__(self, input_shape, rank):
        """
        input_shape : tuple
        Ex. (3,28,28)
        """
        super(Model, self).__init__()

        l, m, n = input_shape
        self.input_shape = input_shape
        self.rank = rank

        self.U = torch.nn.Parameter(torch.randn(rank, l)/100., requires_grad=True)
        self.V = torch.nn.Parameter(torch.randn(rank, m)/100., requires_grad=True)
        self.W = torch.nn.Parameter(torch.randn(rank, n)/100., requires_grad=True)

    @staticmethod
    def kronecker_product(t1, t2):
        """
        https://discuss.pytorch.org/t/kronecker-product/3919/5

        Computes the Kronecker product between two tensors.
        See https://en.wikipedia.org/wiki/Kronecker_product
        """
        t1_height, t1_width = t1.size()
        t2_height, t2_width = t2.size()
        out_height = t1_height * t2_height
        out_width = t1_width * t2_width

        tiled_t2 = t2.repeat(t1_height, t1_width)
        expanded_t1 = (
            t1.unsqueeze(2)
              .unsqueeze(3)
              .repeat(1, t2_height, t2_width, 1)
              .view(out_height, out_width)
        )

        return expanded_t1 * tiled_t2

    def forward_one_rank(self, u, v, w):
        """
        input
            u : torch.FloatTensor of size l
            v : torch.FloatTensor of size m
            w : torch.FloatTensor of size n
        output
            outputs : torch.FloatTensor of size lxmxn
        """
        A = self.kronecker_product(u, v)
        output = self.kronecker_product(A, w)
        return output

    def forward(self):
        l, m, n = self.input_shape
        output = self.forward_one_rank(self.U[0].unsqueeze(1), self.V[0].unsqueeze(1), self.W[0].unsqueeze(1))

        for i in np.arange(1, self.rank):
            one_rank = self.forward_one_rank(self.U[i].unsqueeze(1), self.V[i].unsqueeze(1), self.W[i].unsqueeze(1))
            output = output + one_rank
        return output

これは，クロネッカー積でテンソル分解を実装している．クロネッカー積の実装はここのものをそのまま使ってる．

class Model(nn.Module):
    def __init__(self, input_shape):
        """
        input_shape : tuple
        Ex. (3,28,28)
        """
        super(Model, self).__init__()

        l, m, n = input_shape
        self.input_shape = input_shape

        self.U = torch.nn.Parameter(torch.randn(l)/100., requires_grad=True)
        self.V = torch.nn.Parameter(torch.randn(m)/100., requires_grad=True)
        self.W = torch.nn.Parameter(torch.randn(n)/100., requires_grad=True)

    def forward(self):
        l, m, n = self.input_shape
        output = Variable(torch.zeros((l,m,n)))
        for i in np.arange(l):
            for j in np.arange(m):
                for k in np.arange(n):
                    output[i,j,k] = self.U[i] * self.V[j] * self.W[k]
        return output

これはfor文で愚直にやるやつ．このコードはrank１にしか対応していないのと，めちゃくちゃ遅いのでオススメしない．