pytorchで行列分解 〜行列分解をふんわり理解する〜

はじめに

IBIS2017のチュートリアルで，林先生が「テンソル分解をニューラルネットのフレームワークでやれば楽チンではないか」みたいなことを言っていて，確かに便利そうだと思ったのでそれを試す．

ここではフレームワークとしてpytorchを使う．

まずは前段階として単純行列分解をやってみる．
テンソル分解はそのうちやりたい．（余裕があれば ）
テンソル分解もpytorchでテンソル分解（CP分解）でやった．

環境

• Python 3.6.1
• torch (0.2.0.post3)
• torchvision (0.1.9)

モデルの定義

$X$を$U V^{T}$に分解することを考える．$X$が(n,m)行列のとき，Vは(n,r)行列，Vは(m,r)行列になる．

import torch
from torchvision import datasets, transforms

from torch.autograd import Variable
import torch.nn as nn
import torch.optim as optim
import numpy as np

import matplotlib.pyplot as plt

class Model(nn.Module):
    def __init__(self, input_shape, rank):
        """
        input_shape : tuple
        Ex. (28,28)
        rank : int
        """
        super(Model, self).__init__()
        n, m = input_shape
        self.input_shape = input_shape
        self.rank = rank
        self.U = torch.nn.Parameter(torch.randn(n, rank), requires_grad=True)
        self.V = torch.nn.Parameter(torch.randn(m, rank), requires_grad=True)

    def forward(self):
        outputs = torch.mm(self.U, self.V.t())
        return outputs

forwardにはデータXを渡していないことに注意．

データの取得

train_loader = torch.utils.data.DataLoader(
    datasets.MNIST('./data', train=True, download=True,
                   transform=transforms.Compose([
                       transforms.ToTensor(),
                       transforms.Normalize((0.1307,), (0.3081,))
                   ])),
    batch_size=1, shuffle=True)

train_loader_iter = iter(train_loader)
data = train_loader_iter.next()[0].squeeze()

normalizeのパラメータはこのMNIST exampleでこのように設定していたのでそのまま使ってる．おそらく経験的にこの値が良いとされた正規化パラメーターであろう．

データを一つサンプリングして，それを二つの行列に分解する．

サンプリングしたデータを試しにプロットする．

plt.imshow(data.numpy())
plt.show()

loss, optimizerの定義

def my_mseloss(data, output):
    """
    input
        data : torch.autograd.variable.Variable
        output : torch.autograd.variable.Variable
    output
        mse_loss : torch.autograd.variable.Variable
    """
    mse_loss = (data - output).pow(2).sum()
    return mse_loss
  
input_shape = (28,28)
rank = 10

model = Model(input_shape, rank)
optimizer = optim.SGD([model.U, model.V], lr=0.001, momentum=0.9)

data = Variable(data)

ここでは適当にランクは10で行う．
optimizerも適当で，SGDである深い意味はない．

訓練

for batch_idx in np.arange(1000):
    optimizer.zero_grad()
    output = model()
    loss_out = my_mseloss(data, output)
    loss_out.backward()
    optimizer.step()

    if batch_idx % 10 == 0:
        print(f'index : {batch_idx}, Loss: {loss_out.data[0]}')

速攻でロスが一定になる．

プロット

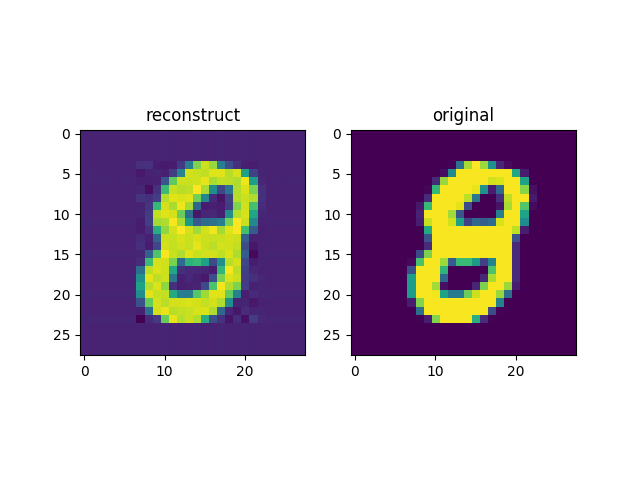
元の画像と復元した画像のプロット

U = model.U.data.numpy()
V = model.V.data.numpy()

X_hat = np.dot(U, V.T)

fig = plt.figure()
ax1 = fig.add_subplot(121)
plt.imshow(X_hat)
ax2 = fig.add_subplot(122)
plt.imshow(data.data.numpy())
fig.show()

なかなか再現されている．

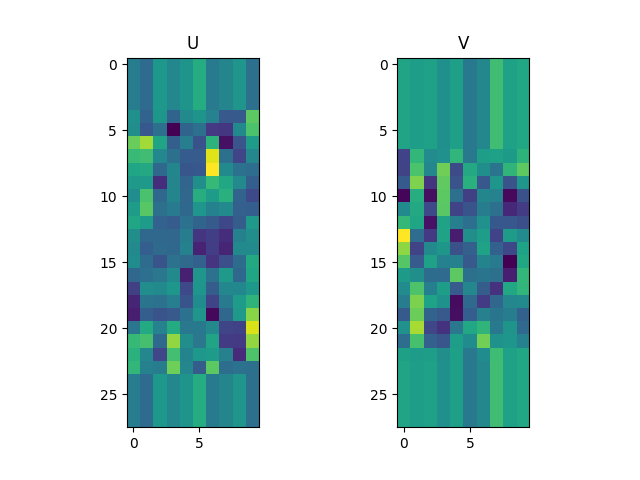
分解した行列U, Vのプロット

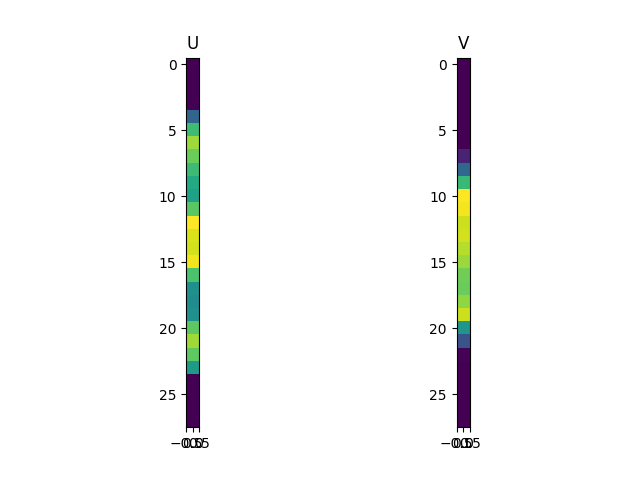
UとVがどんな行列か見てみる．

fig = plt.figure()
ax1 = fig.add_subplot(121)
plt.imshow(U)
ax1.set_title("U")
ax2 = fig.add_subplot(122)
plt.imshow(V)
ax2.set_title("V")
fig.show()

UとVがどういう行列なのか，なんだかよく分からない．

ランク１でプロットしてふんわり理解する

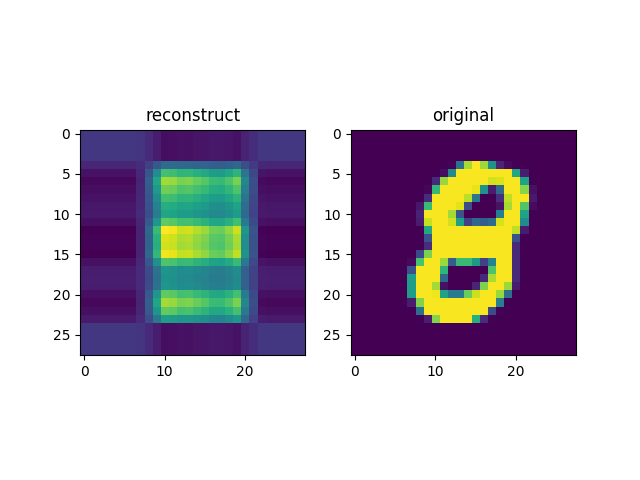
こういう時は大体極端なケースを考えれば，理解の手助けになるので，ランク１でやってみる．

あまり復元できていない．
3か8のどちらかだろうということはわかりそう．

$U$と$V$をプロットしてみると，こんな感じになっていた．

ランクが１のとき，

|X - UV^{T}|^{2}_{Fro}

の１列目のみに着目すると，

|{\bf x}_{1} - v_{1} U|_{2}^{2}

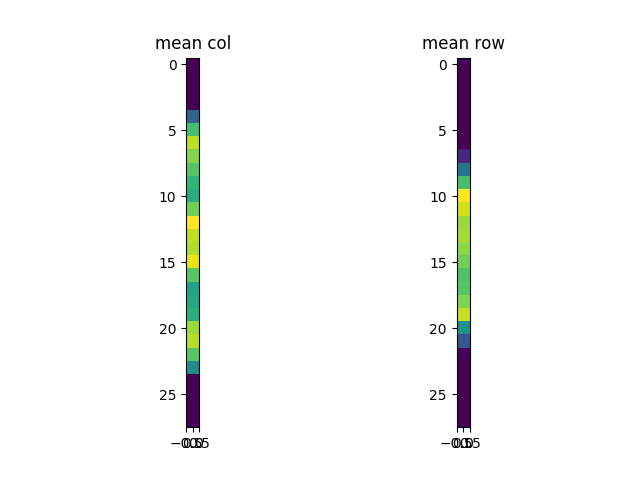
となっており，最適解では一階微分が０となっているはずなので，それを$v_{1}$について解くと，$v_{1}$は${\bf x}_{1}$の和に比例することがわかる．この時，$U$については固定しているので，正確な関係性ではないが，Vは行に対して平均を取ったものと似たようなものになりそうだなぁということが推測される．実際に見てみると割と似てる．

d = data.data.numpy()

fig = plt.figure()
ax1 = fig.add_subplot(121)
plt.imshow(d.mean(0).reshape(len(d),1))
ax1.set_title("mean row")
ax2 = fig.add_subplot(122)
plt.imshow(d.mean(1).reshape(len(d),1))
ax2.set_title("mean col")
fig.show()

$U$については今度は$V$を固定して同じことを考えると，列に関する平均とだいたい似ていることになる．

そんなわけで，Uは横方向の情報を圧縮していて，Vは縦方向の情報を圧縮しているんだなあとぼんやり思う．
そこで，情報としては特に増やさず，形だけUとVをそれぞれ28*28にしてみる．
そして，それらの要素の積でXが再現されるので，それを見比べてみる．

one_mat = np.ones(U.size).reshape(U.shape)
U_ = np.dot(U, one_mat.T)
Vt_ = np.dot(one_mat, V.T)

X_ = U_ * Vt_

from matplotlib import colors

cmap = plt.get_cmap("bwr")
ticks = np.array([-4, 0, 4])
bounds=np.arange(ticks.min(), ticks.max(), 0.1)
norm = colors.BoundaryNorm(bounds, cmap.N)

fig = plt.figure()
ax1 = fig.add_subplot(141)
plt.imshow(U_, cmap=cmap, norm=norm)
ax1.set_title("U_")
ax2 = fig.add_subplot(142)
plt.imshow(Vt_, cmap=cmap, norm=norm)
ax2.set_title("Vt_")
ax3 = fig.add_subplot(143)
plt.imshow(X_, cmap=cmap, norm=norm)
ax3.set_title("reconstruct2")
ax4 = fig.add_subplot(144)
cax = plt.imshow(data.data.numpy(), cmap=cmap, norm=norm)
ax4.set_title("original")
plt.colorbar(cax, cmap=cmap, norm=norm, boundaries=bounds, ticks=ticks)
fig.show()

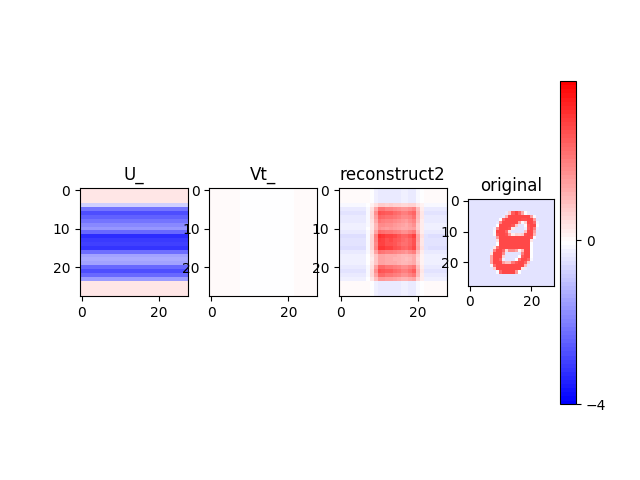
このU_とVt_の要素の積となると格段にわかりやすい気がする．
今まではcolormapが自動的に調整されていたので，相対的な値の関係しかプロットではよく分からなかったが，今度は値の大きさもちゃんと見る．
このプロットから，U_が値の大きさをほぼ全て受け持ち，Vt_は何もしてないじゃんという気になるが，符号だけに着目してプロットして見ると，以下のようになる．

cmap = colors.ListedColormap(['blue', 'red'])
bounds=[-1,0,1]
norm = colors.BoundaryNorm(bounds, cmap.N)

fig = plt.figure()
ax1 = fig.add_subplot(141)
plt.imshow(U_, cmap=cmap, norm=norm)
ax1.set_title("U_")
ax2 = fig.add_subplot(142)
plt.imshow(Vt_, cmap=cmap, norm=norm)
ax2.set_title("Vt_")
ax3 = fig.add_subplot(143)
plt.imshow(X_, cmap=cmap, norm=norm)
ax3.set_title("reconstruct2")
ax4 = fig.add_subplot(144)
cax = plt.imshow(data.data.numpy(), cmap=cmap, norm=norm)
ax4.set_title("original")
plt.colorbar(cax, cmap=cmap, norm=norm, boundaries=bounds, ticks=[-1, 0, 1])
fig.show()

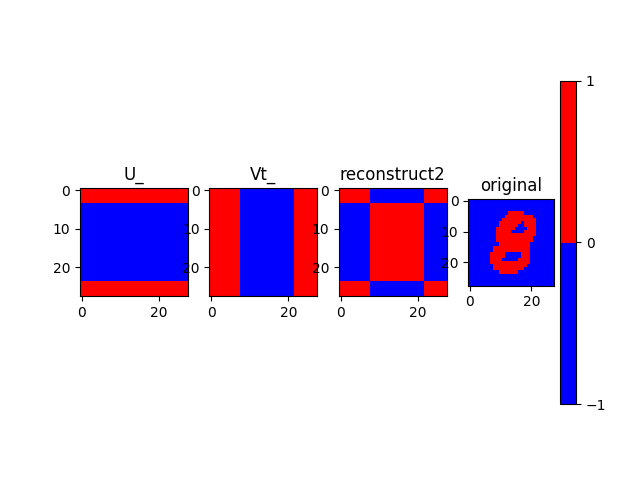
目に優しくないプロットになったが，真ん中の部分だけ，マイナス×マイナスでプラスにしていることがわかる．つまり符号による調整をVt_が受け持っているんだなぁとわかる．
ついでに，数字のない四隅の部分にメッシュが入っていた理由もこれからわかる．

というわけで行列分解では，

• Uが横方向の情報を持ち，Vが縦方向の情報を持ってる．
• 値の管理と符号による調整という役割分担みたいなものも生じている．
  ということがふんわりわかった．

終わりに

• 確かになかなか楽に実装できる．
• プロットによる説明になったが，実際は単純行列分解はランクをあるrに固定し，固有値を全て１とした特異値分解として解釈するのがいい予感がする．（実際にそうなのかいい文献などあったら教えてください．）