#前書き
高校数学で学習する「集合と論理」が扱う分野について、
- 今一つ自分の中で消化しきれない
- 言われればわかるがうまく運用できない
というモヤモヤを常日頃考えていました。
何とか上手く消化できるモデルはないかと考えていたときに、
今回紹介する「紙と針のモデル」（長いので以降これを
「PPモデル（Paper and Pin Model）」と呼ぶ）を考案したので、
それがどれくらい有用なのかを、記事を書きながら確認しようと思い至りました。
#PPモデル
登場人物は以下の2つ
- 紙
- 針（まち針のような針）
です。
紙が集合を、針が要素を、それぞれ意味していると考えます。
「要素aが集合Aに含まれている（a∊A）」ことは、
「針aが紙Aに刺さっている」ことと対応します。
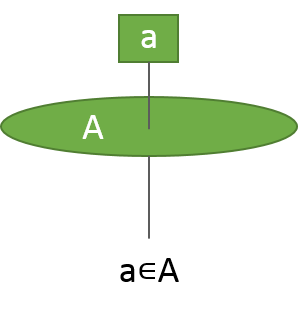
逆に、
「要素aが集合Aに含まれていない（a∉A）」ことは、
「針aが紙Aに刺さっていない」ことと対応します。
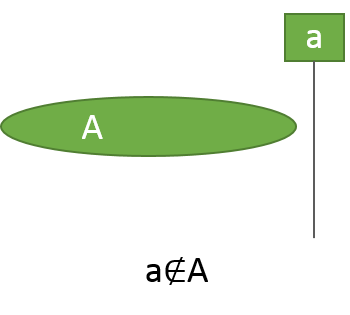
この紙と針は、各々が意味する集合、要素に応じて、配置される位置は確定します。
好き勝手に紙に針を刺すことはできません。
紙が意味する集合、針が意味する要素に応じて、
紙に針が刺さるのか、刺さらないのかが決まります。
以下に、その実例を紹介いたします。
##実数のPPモデル
実数のような、大小関係がある要素を考えるときは、
数直線をイメージできるように、細長い紙で集合を表すと使いやすいです。
（私はこれを「紙テープ」と呼んでいます）
さて、実数Rの紙テープは以下のようになります。
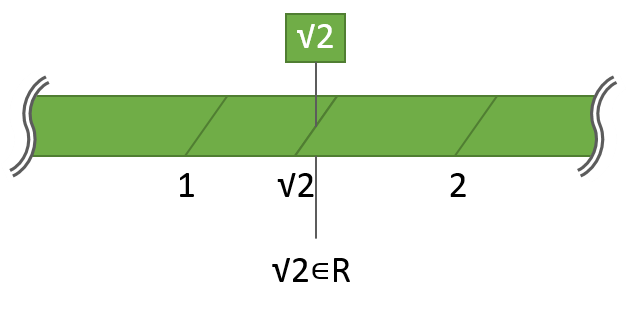
紙テープの上には、各実数に一対一で対応する位置があります。
0の位置、1の位置、√2の位置、などなど。
さて、ここで要素1について考えると、これは針1に対応します。
この針1は、紙テープの1の位置に刺さることになります。
針√2は、紙テープの√2の位置に刺さります。
さて、ここで、実数Rの部分集合として、集合S={x: x∊[-1, 1]}を考えてみます。
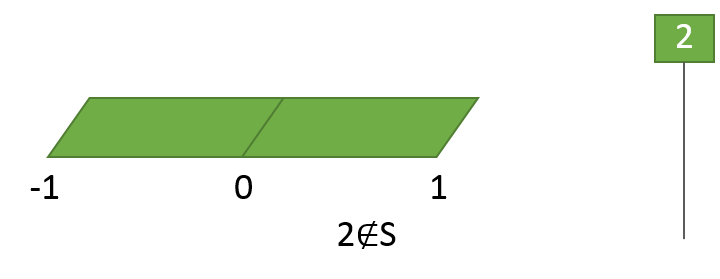
集合Sに対応するPPモデルは、-1から1までの短い紙テープになります。
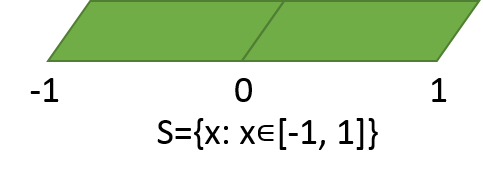
この集合Sの要素に対応する針は、この短い紙テープに刺さることができます。
例えば、0の針、1の針、-1の針、1/2の針は、この紙テープに刺さります。
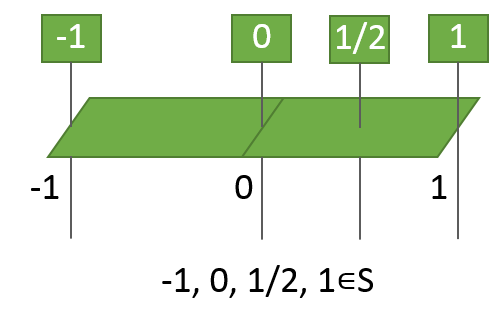
（-1や1は、紙テープの端にギリギリで刺さっている、というか、かすっているイメージ）
しかし、集合Bの要素ではない、例えば2の針は、
この紙テープには刺さりません。
##集合同士の関係
さて、今度は、字数の集合Rの紙テープと、
その部分集合Sの紙テープの関係について考えて見ましょう。
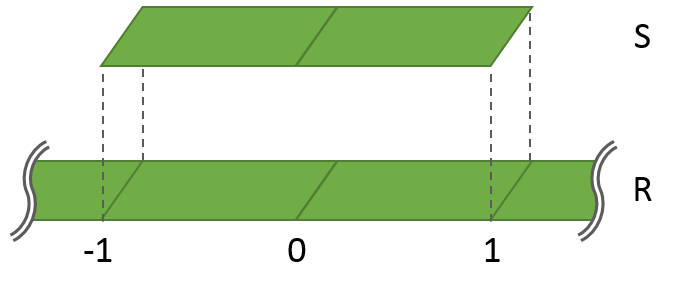
集合Rの紙テープの上に、集合Sの紙テープを重ねてみると、
紙テープSは紙テープRの上に、はみ出ることなく重なることができます。
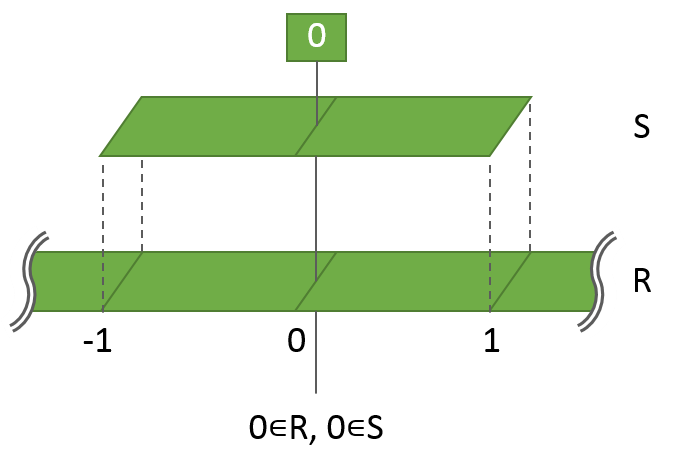
ここで、RとSの両方の要素である0の針を刺してみると、
当然、RとSの両方に刺さります。
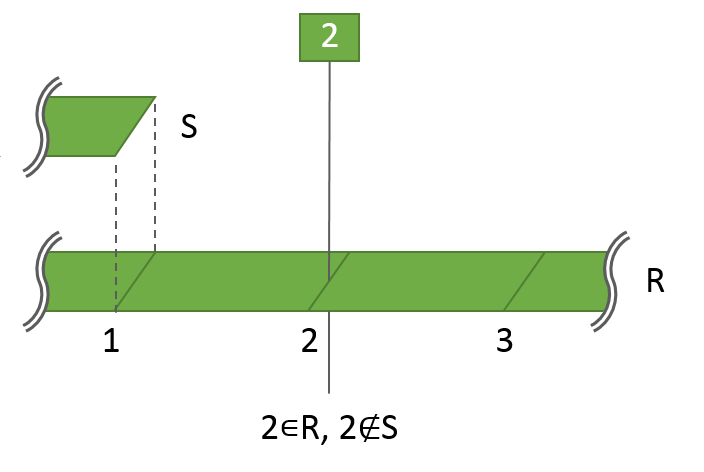
一方で、Rの要素ではあるがSの要素ではない2の針を刺してみると、
これも当然、Rには刺さりますがSには刺さりません。
集合Sのすべての要素、すなわち、紙テープSに刺さるすべての針について考えると、
紙テープSは紙テープRの上にはみ出ることなく重なっているので、
紙テープSに刺さるすべての針は、すべて紙テープRに刺さります。
数学的に言い直せば、
集合Sは集合Rの部分集合である（S⊂R）から、
集合Sの要素sはすべて、集合Rの要素である（∀s∊S, s∊R）、ということです。
一般化すると、
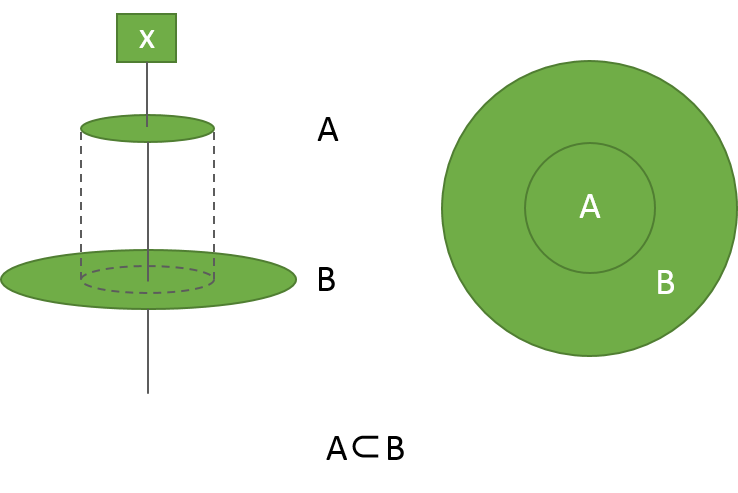
集合Aが集合Bの部分集合であるとき（A⊂B）、
PPモデルでは、紙Aは紙Bにはみ出すことなく重なります。
この時、針xが紙Aに刺さるのであれば、針xは必ず紙Bにも刺さります。
ちなみに、同様の関係をベン図を使って示すと、図の右側ようになり、
PPモデルを上から見たものがベン図である、とみなすことができます・
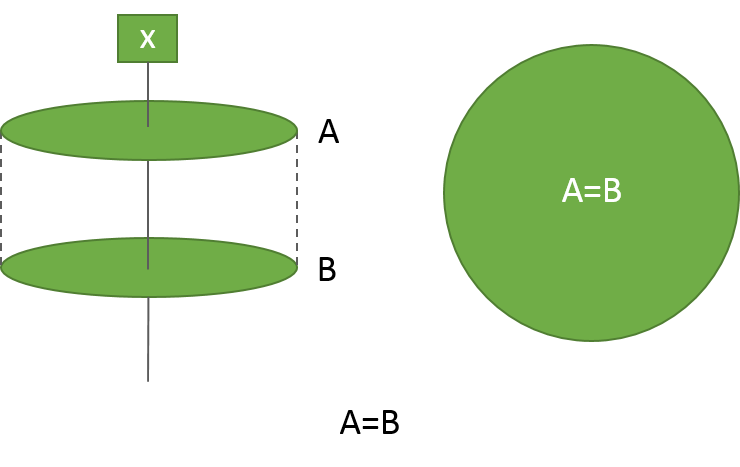
なお、集合Aが集合Bと一致するとき（A＝B）、
PPモデルでは、紙Aと紙Bは同じ大きさになり、ぴったり重なることになります。
勿論、針xが紙Aに刺さるのであれば、針xは必ず紙Bにも刺さります。
##事例
まずは、部分集合の例をいくつか挙げてみます。
###例1: 実数Rと正の実数R+
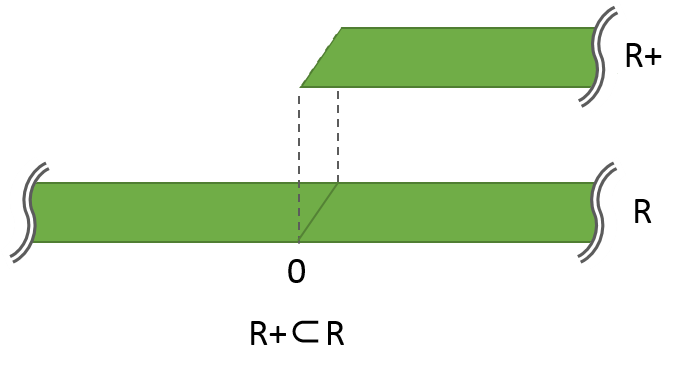
正の実数の集合R+は、実数の集合Rの部分集合であり（R+⊂R）、
確かに、紙R+は紙Rにはみ出ることなく重なります。
（集合R+には要素0は含まれないので、紙テープR+の0の部分は破線になっています）
###例2: 実数Rと整数Z
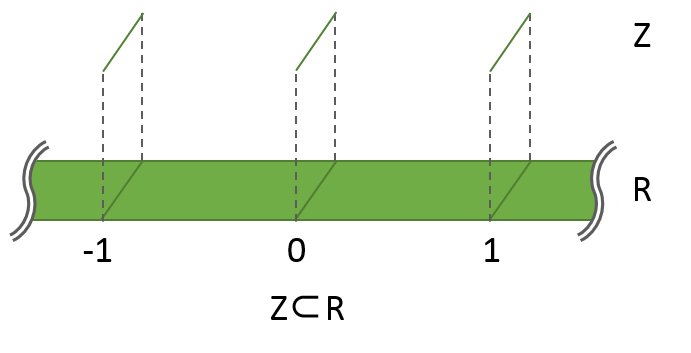
整数の集合Zは、実数の集合Rの部分集合です（Z⊂R）。
実数が連続的な値（連続値）であるのに対し、整数は離散的な値（離散値）ですので、
PPモデルでは、実数Rを紙テープで表すと、整数Zは、等間隔に並ぶ線になります。
この形であっても、確かに、紙Zは紙Rにはみ出ることなく重なります。
###例3: 自然数Nと素数P
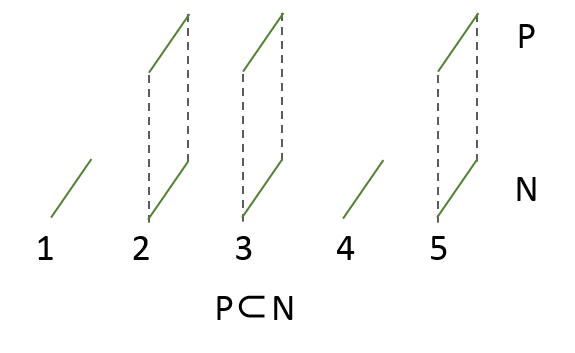
素数の集合Pは、自然数の集合Nの部分集合です（P⊂N）。
例2における整数の集合Zと同様、自然数Nも素数Pも離散値なので、
今までと同じようにPPモデルで表現すると、
両方とも線の配列で表されることになります。
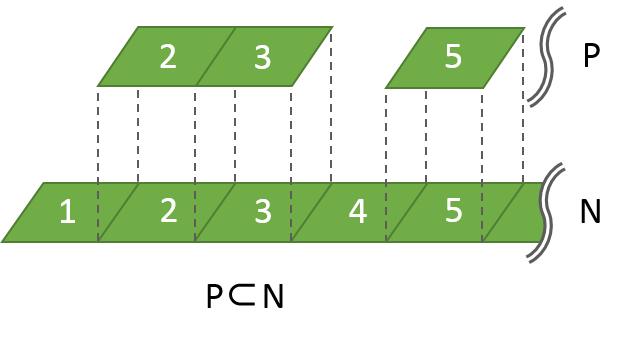
離散値を要素とする集合を扱うのであれば、
下図のように、紙テープを等間隔に分割したモデルで考えても良いでしょう。
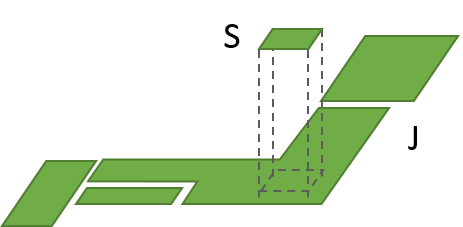
###例4: 日本国Jと埼玉県S
地点を要素、領域を地点の集合と考えれば、
埼玉県S、日本国Jはともに集合と考えることができます。
この時、埼玉県Sは日本国Jの部分集合になります（S⊂J）。
次は、部分集合ではない例をいくつか挙げてみます。
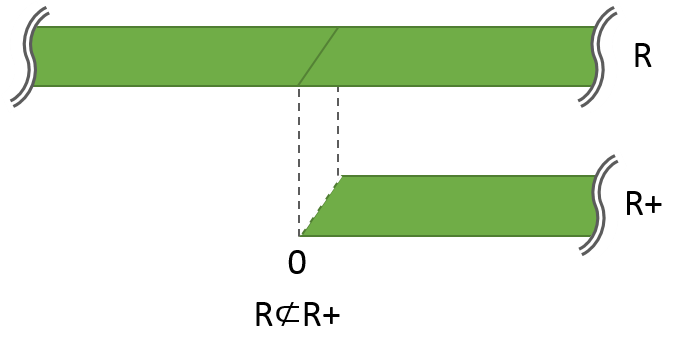
###例5: 正の実数R+と実数R
実数の集合Rは、正の実数の集合R+の部分集合ではありません（R⊄R+）。
確かに、紙Rを紙R+に重ねると、一部はみ出ています。
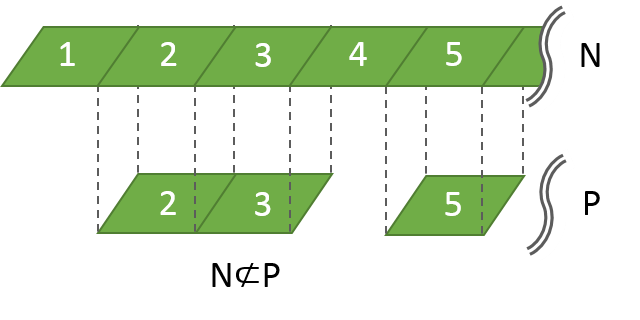
###例6: 素数Pと自然数N
自然数の集合Nは、素数の集合Pの部分集合ではありません（N⊄P）。
確かに、紙Nを紙Pに重ねると、一部がはみ出してしまいます。
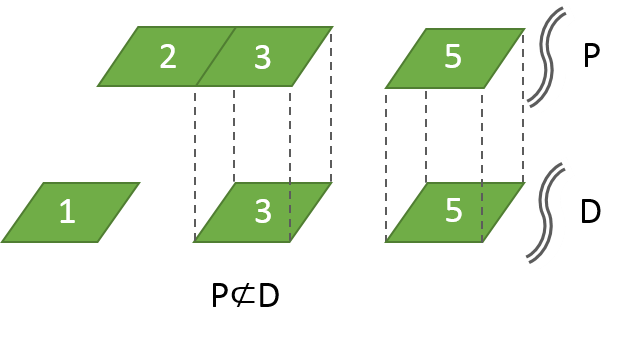
###例7: 奇数Dと素数P
素数の集合Pは、奇数の集合Dの部分集合ではありません（P⊄D）
（2だけが唯一、素数であり奇数でない数）
確かに。紙Pを紙Dに重ねると、2だけがはみ出します。
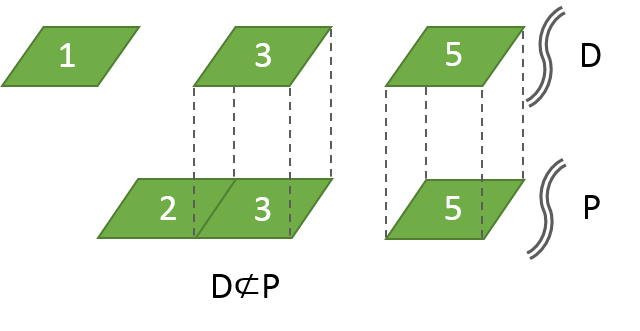
この例については、奇数と素数の関係を逆にしても、部分集合の関係にはなりません。
つまり、奇数の集合Dも、素数の集合Pの部分集合ではなく（D⊄P）、
これも、紙Dを紙Pに重ねると、はみ出る数字が発生します。
（図中では1がはみ出ていますが、素数でない奇数は9、15、21と、無数にありますし、
奇数は負数も含みますので、負の奇数はすべて、素数でない奇数になります。）
###例8: 埼玉県Sと秩父多摩甲斐国立公園C
秩父多摩甲斐国立公園は、東京都、埼玉県、山梨県、長野県の1都3県にまたがっている
国立公園です。
ですので、秩父多摩甲斐国立公園Cは、埼玉県Sの部分集合ではありません（C⊄S）。
埼玉県域すべてが、同公園に指定されているわけでもありませんから、
埼玉県Sも、秩父多摩甲斐国立公園Cの部分集合ではありません（S⊄C）。
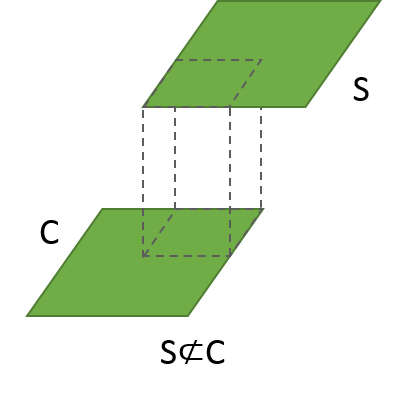
このような、紙の重ね合わせは、3つ以上の集合でも行えます。
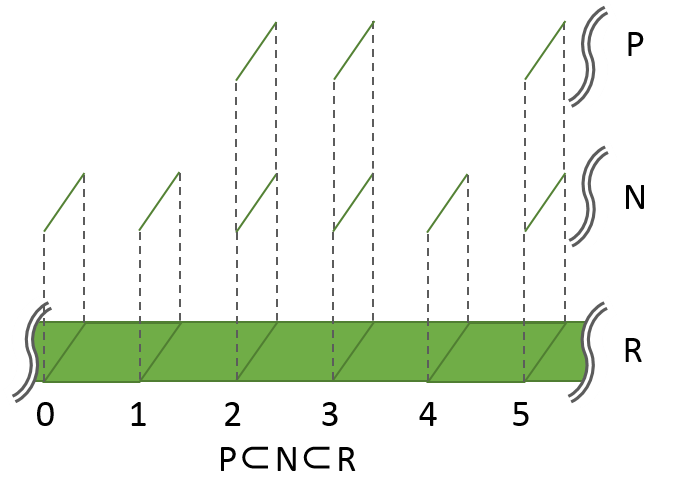
###例9: 実数Rと自然数Nと素数P
この3つの集合は、P⊂N⊂Rの関係にあります。
PPモデルで表すと、上の紙は下の紙からはみ出さず重なることが確認できます。
###例10: 地球Eと日本国Jと埼玉県S
この3つの集合も、S⊂J⊂Eの関係にあります。
PPモデルで表すと、上の紙は下の紙からはみ出さず重なることが確認できます。
#後書き
次回はこちら：
紙と針のモデルで命題を考える（PPモデルで集合と論理を考える#2）