【代数学】ゲームプログラマのための代数学 集合と写像

モチベーション

去年から仕事でデータの暗号化周りを触る機会があり、ちょっとした好奇心でAES暗号の作りを見てから暗号理論に興味が湧いた。

具体的には有限体(もしくはガロア体とも言う) $GF(p^n)$ の構造に興味を持った。
このガロア体は素数pの剰余値で作られた有限の集合であり、例えばpが5である場合、 {0, 1, 2, 3, 4} という要素を持った集合になる。
この集合の演算は p の剰余値のみで演算する必要があるので、例えばpが5なら 4 + 1 をすると 5 ではなく 0 になる。

この有限体は四則演算において閉じており、また全ての要素は p-1乗すると 1 になる
これはフェルマーの小定理で定義されていることではあるのだが、有限体を「拡大」するともっと面白いことになる。
この有限体は次数 n の既約多項式を用いることで $p^n$ 個の要素を持つ有限体に 「拡大」 させる事ができる。
この拡大された有限体を「拡大体」などと呼ぶ。

既約多項式とはこれ以上因数分解できない多項式のことで、整数の世界における素数に近い。
逆に因数分解できる場合は「可約」であると言う。
拡大体はこの既約多項式と割り算をした余りの値を要素とする集合であり、また全ての要素に対して $a^{p^n−1}=1$ が成立する。
AES暗号の SBox 置換テーブルはこの性質を利用しており $GF(2^8)$ における乗法逆元に置換している。
もう少し具体的には $x^8 + x^4 + x^3 + x + 1$ という既約多項式を法として体を位数2から $2^8$ (つまり要素数256個)まで拡大する。

前述した通り、この拡大体はどの要素 a を取っても $a^{255} = 1$ になる世界なので $a^{254}$ が逆元になる。

これは拡大体が体の性質を持っており、乗法において位数 $p^m-1$ の巡回群の構造を持っているからであるわけなのだが
この構造の性質を理解する為には群の構造や環におけるイデアル、多項式環について知る必要があった。
(具体的には環論において既約多項式による生成イデアルは極大イデアルになり、極大イデアルの商環は体になるという定理があり、この定理によって既約多項式による拡大体 $GF(p^m)$ は常に体になるというような話があるが、この辺りは自分もまだ理解が足りないのでシッカリと説明できません。まだ勉強が必要)

このように、暗号理論は代数学の知識が必要であるのだが、だいたいの暗号理論系の書物を読むと代数学の知識があることは大前提になっているので、まずは触り程度でも代数学を学ばないと読むことができないと感じた。 当初は暗号理論に興味があって代数学を勉強していたが、自分が想像していた以上にプログラミングにも大きく関わってきたり、理解しておくと把握しやすい概念がある事にも気づいた。

この記事では主にそういった点について触れたいと思う。

集合について

代数学では 「ある集合」 と 「その集合の要素」 との関係性についてを考える
この「集合」はエンジニア目線で見ると「配列」に似ている。
配列は要素が重複していても良いが集合では重複はないという点で異なるので、配列と集合は等価ではないが、重複なしのコレクションと考えると取っ付きやすいかもしれない。
いわゆる Javascript の Set、C#の HashSet、python で言えば numpy の np.unique などだ。

しかし実際には配列だけではなく、それ以外の様々な概念を「集合」として考えることができる。
例えば、 以下のような関数があることを考えてみよう。

def F(X: list) -> bool:
  for x in X:
    if not P(x):
      return False
  return True

このとき、この P が true か false を返す関数であるということがわかるが、このとき引数 x は以下のどちらかの集合に属していると言える。

1. P(x) が true を返す値の集合
2. P(x) が false を返す値の集合

論理学ではこのような True か False かを返す条件式の事を 「命題」 と呼ぶ。
例えばこのような関数Fを考える場合、論理学的には「全ての X の要素である x に対してP(x) が成り立つならば真である」 というような言い方になる。
上記のような 「X の要素 x」 とは数学では x∈X のように表記する。
「全てのXの要素xに対し」 とは数学では ∀x∈X と書かれる
∀ は全称記号と呼ばれるもので「任意の〜に対し」というような意味になる。

「任意の〜」 というと any を思い出すところから 「一つでも条件が一致していればいいのか？」 と考えてしまった事がある。
しかし、ここでの any は関数の any, all とは少し異なる。
数学や論理学で「任意の X の要素 x に対し」 という場合、
これは「Xの中のどのような要素を x として取っても」という意味合いになる。
つまり 「どれを取っても条件が成立すること」 と言っている

条件 P はなんでも良いが、例えばここでは 「x が 3 の倍数であれば True」 としてみよう

def P(x):
  return x % 3 == 0

そして以下のように関数を呼び出してみる。

print(f"結果: {F([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])}")
print(f"結果: {F([3, 6, 9, 12, 15])}")
# 結果: False
# 結果: True

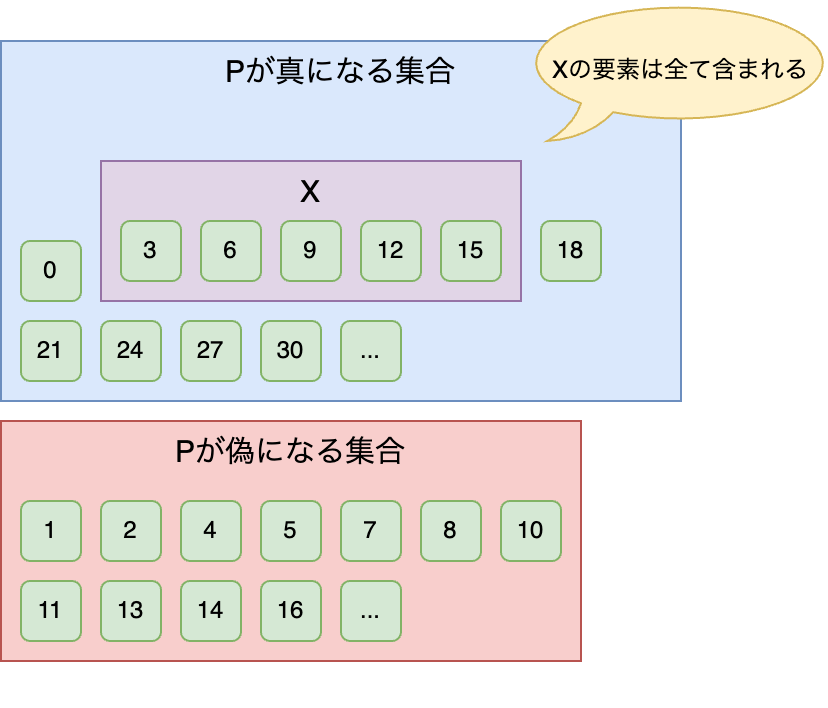
このとき、「集合」という概念で考えると次のようにも考えられる。

Xの全ての要素が P(x) の条件を満たすとは、 X は P(x) を真とする要素で作られた集合の部分集合である

「x % 3 == 0 のときに真になる」という集合を図にすると以下のようになる。

このようなとき真であるといい

Xが 「部分集合」 であるにはXの全ての要素がその集合の要素である必要があるので、このようなときは偽である

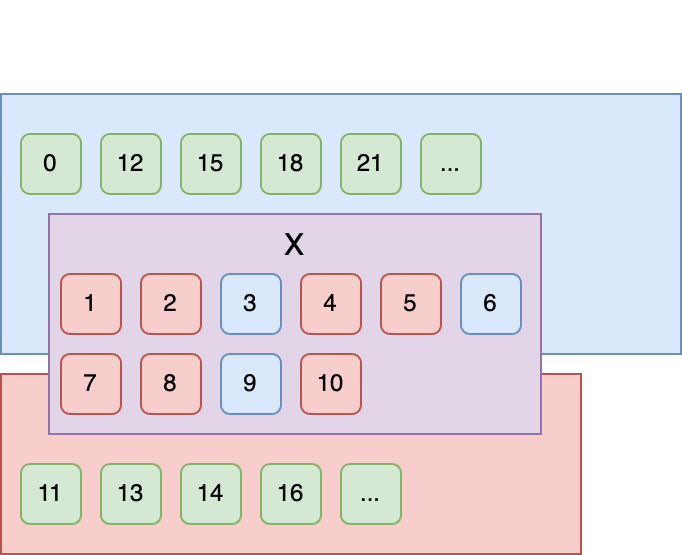
また、以下のようなケースのときも数学的には True となる。

print(f"結果: {F([])}")
# 結果: True

これは vacuous truth （空虚な真）という論理学でしばしば登場する話で
空集合は特定の条件を満たさないので、命題が自動的に真となることを言う
空虚な真(Wikipedia)

「条件を満たす集合の部分集合であるとき、真である」という事は
空集合はどの集合の部分集合でもあるので真となる

※集合 φ が ある集合 A の部分集合であるためには「φ の要素は全て Aの要素である」必要がある
つまり「φに一つでも A にはない要素が含まれている」のであればそれは部分集合にならない。
このとき、もし集合φが空集合であるとき、空集合は要素を持たない集合であるので A にはない要素が含まれていない。
したがって 「φに一つでも A にはない要素が含まれている」 が成立しないので結果的に空集合はAの部分集合であると言える

この他にも、以下のようなものも集合の一つである
これは特殊直交群(回転群)と呼ばれるもので線型代数に登場するが、回転行列を要素に持つ集合である

写像について

代数学には「写像」と呼ばれる概念が存在する。
これは「ある集合の要素と別の集合の要素を結びつける」というものである。
いきなり写像！ と言い出してもなんのこっちゃとなってしまうので、写像とは以下の図のような対応関係であると言えばどうだろう

このとき、 f(x) に 1 を指定したら "a" という文字が手に入る
同様に f(x) に 2 を指定すると "b" であり、以下も同様に対応付けされている。
これはプログラマ的に言えば C# なら Dictionary であり python であれば dict であり, C/C++ やJavascript で言うなれば map といった概念と全く同じであるという事に気づく。

実際、写像を英語にすると map になることからも、C++の std::map や Javascript の map 型 に馴染みがあれば意味はなんとなく「ああ、そういうことね！」となるのではないだろうか。

また、 f(x) という名前からなんとなく想像がつくかもしれないが、数学に登場する関数も写像である。
(「写像は関数のようなもの」と表現するのはあまり適切ではないので、このように表現しています)
写像には全単射、全射、単射などがあるのだが、長くなるのであまりここでは深掘りしない。
ちなみに上図のような各要素が１体１で対応しているものは全単射と呼ばれる。

行列は写像

ゲームプログラマーであれば馴染みが深いかもしれないが、「行列」も写像である。
行列は線形代数における線形写像と呼ばれる写像であり、この行列計算を行う写像をここでは例えば $M$ と呼んでみよう。
行列に引数として渡す三次元ベクトルを $v$ 、ベクトル値だけを集めたベクトルの集合(これをベクトル空間と呼ぶ) を $V^3$ と呼ぶのなら、数学的には

$M(v):V^3→V^3$
と表すことができる

これは「三次元ベクトル空間 $V^3$ に属する要素を関数 $M$ の入力値として渡すと、同じベクトル空間 $V^3$ に属する要素として返す」
という意味になる。

ゲームプログラミングで使う範囲の行列の計算は基本的に「あるベクトルを別のベクトルに変換する」という操作を主としているのでこのような書き方になるのだが、線形変換は必ずしも同一の集合同士を対応付けするとは限らない。
(このように入力も出力も同じ集合の要素になるような変換は 自己同型 と呼ばれる)

例えば入力値と出力値の集合が違うケースとして以下のようなケースがある。
$M(v): V^3→V^2$
これは「三次元ベクトル空間 $V^3$ を行列 $M$ のパラメータに渡すと二次元のベクトル空間 $V^2$ に変換した値を結果として返す」という意味になる。
これの有名な例は三次元空間の物体を二次元の平面として書き出す「射影変換」である。

写像の合成

写像には 合成　という概念があり、例えば 写像f, g というのがあるとき f ○ g などのように表すことが出来る。
この写像の合成とは「f と g を合成して作られた f ○ g という写像は f と g　の演算結果を一度に得られる」ものになる。

この写像の合成をプログラミングに置き換えると以下のような感じだろうか

# ある数 x を２乗する二次関数
# f(x) = x^2
def f(x):
    return x * x

# 一次関数
# g(x) = 2x - 3
def g(x):
    return (2 * x) - 3

# 引数で渡された関数を合成する
def synthesis(f, g):
    def new_func(x):
        return f(g(x))
    return new_func

# 関数の合成
h = synthesis(f, g)

print(f"f ○ g = {h(10)}")
# ① x は g で計算され、17を返す
# ② f は x(=17) を受け取り、二乗にして返す
# ③ 結果は 289 である

f ○ g は 上記のように「 g で評価したものを f で評価する」事と同じである。

この写像の合成は当然行列でも使える。
例えば、２次元で拡大縮小を行った後に回転を行い、最後に並行移動を足すようなアフィン変換を書いてみよう。
numpy で行列計算が行えるので試しにnumpyを使ってみる

@dataclass
class Vec2:
    x: float
    y: float

# 回転行列
def rotate_matrix(x):
    return np.array([
        [cos(x), -sin(x), 0],
        [sin(x),  cos(x), 0],
        [     0,       0, 1],
    ])

# 拡大・縮小行列
def scale_matrix(scale: Scale):
    return np.array([
        [scale.x,       0, 0],
        [      0, scale.y, 0],
        [      0,       0, 1],
    ])

# 並行移動行列
def translate(x, y):
    return np.array([
        [1, 0, x],
        [0, 1, y],
        [0, 0, 1]
    ])

上記行列の積を 拡縮→回転→並行移動 の順番で合成している。
TRS は合成された行列になるのでこれとベクトルをかけるだけで 拡縮→回転→並行移動 まで行える

R = rotate_matrix(deg2rad(self.rotation))
S = scale_matrix(self.scale)
T = translate(self.pos[0], self.pos[1])
TRS = np.dot(T, np.dot(R, S))
w = self.width / 2
h = self.height / 2
v1 = np.dot(TRS, [- w, - h, 1])
v2 = np.dot(TRS, [ +w, - h, 1])
v3 = np.dot(TRS, [ +w, + h, 1])
v4 = np.dot(TRS, [- w, + h, 1])

例えば拡大縮小行列 S と並行移動行列 T と回転行列 R が存在し、これらを合成した行列 (T ○ R ○ S)は拡大縮小→回転→並行移動 までの変換を一度に行なってくれる。
合成写像の最も身近な例は Unity のシェーダーにある UNITY_MATRIX_MVP という変数で、これは事前にModel, View, Projection の行列を合成してくれている。

可換と非可換

写像は基本的に演算の順序が重要で順序が変わると結果値も変わってしまう
つまり f ○ g と g ○ f は意味として等価ではないことが多い（「ことが多い」というのは一部例外が存在するため）
このようなルールを「交換法則」と呼び、成り立つ場合「可換」、成り立たない場合は「非可換」などと呼ばれたりする。

３Dグラフィックなどに関心のある方であれば行列を触ったことはあると思うが正直な話、私は行列を勉強していた当初「なぜ計算の順番が違うと計算結果が変わるんだ？」と不思議に思っており、つい最近まで行列の計算順序はほとんど暗記していてちゃんと意味を理解していなかった。

代数学ではこの 可換・非可換 という概念が頻繁に登場する。
群、環、体といった構造を理解することで「この演算はどの構造に分類されるのか？」という事を考えるきっかけになったが、この 「演算の構造を理解する」 という工程はベクトルや行列を扱うときに非常に有用であると感じた。

基本的に我々が日常生活で使用する範囲の「実数」の世界で考えた時(日常生活で使うことはないが仮に虚数を追加して複素数まで拡張したとしても)、 a + b や b + a、 ab や ba も意味として等価であり「可換」である事に慣れすぎているので、代数学で「a ○ b = b ○ a が成り立つ時、可換である」などと書かれていても「そんなの当たり前じゃん！」と思うかもしれないのだが、群論や環論などをやって様々な集合や代数的な構造を見てみると意外とこのように 「可換ではない」 構造の計算は沢山存在するのであった (ゲームプログラマに馴染みのある四元数もそんな構造の一つで四元数は「非可換環」に分類される)

恒等写像の存在

例えばある写像 $I$ が $I(v) = v$ となるような性質を持つ場合（つまり何も値が変わらない場合）
この $I$ は恒等写像と呼ばれる。

行列も写像であるので上記の式が成立するような恒等写像が存在する場合があるが、そのときその行列を単位行列と呼ぶ。
単位行列はきわめて単純である

2×2の単位行列

\begin{bmatrix}
1 & 0 \\
0 & 1
\end{bmatrix}

\begin{bmatrix}
x \\
y
\end{bmatrix}

=
\begin{bmatrix}
(1 \times x) + (0 \times y) \\
(0 \times x) + (1 \times y)
\end{bmatrix}

=
\begin{bmatrix}
x \\
y
\end{bmatrix}

3×3の単位行列

\begin{bmatrix}
    1 & 0 & 0 \\
    0 & 1 & 0 \\
    0 & 0 & 1 \\
\end{bmatrix}
\begin{bmatrix}
x \\
y \\
z \\
\end{bmatrix}

=
\begin{bmatrix}
(1 \times x) + (0 \times y) + (0 \times z) \\
(0 \times x) + (1 \times y) + (0 \times z) \\
(0 \times x) + (0 \times y) + (1 \times z) \\
\end{bmatrix}

=
\begin{bmatrix}
x \\
y \\
z \\
\end{bmatrix}

次に $M$ と演算したときにこの計算結果が単位行列である場合、これは逆行列と呼ばれ $M^{-1}$ と書いたりする
つまりこの場合 $MM^{-1} = I$ という関係になる。
この具体例としては例えば二次元の回転行列について考えてみよう。
二次元の回転行列は

\begin{bmatrix}
cos(θ) & -sin(θ) \\
sin(θ) & cos(θ)
\end{bmatrix}

であり、これに対応する逆行列は

\begin{bmatrix}
cos(θ) & sin(θ) \\
-sin(θ) & cos(θ)
\end{bmatrix}

である。
この二つの行列の積を求めると

\begin{bmatrix}
cos^2(θ)+sin^2(θ) & cos(θ)sin(θ)-cos(θ)sin(θ) \\
cos(θ)sin(θ)-cos(θ)sin(θ) & cos^2(θ)+sin^2(θ)
\end{bmatrix}

となる。
$cos^2(θ)+sin^2(θ)$ は 1 であることがわかっている。
ベクトルの長さとして求めても1になるが、仮に $cos(θ)cos(θ)+sin(θ)sin(θ)$ とするとこれは加法定理を使えば $cos(θ-θ)$ となり、 $cos(0)$ 、つまり 1 である。
$cos(θ)sin(θ)-cos(θ)sin(θ)$ に関してはそのまま引き算で=0になるが、
これも加法定理を使っても同様に $sin(θ-θ) = sin(0)$ となるので答えは 0 である
したがってこの行列の計算結果は

\begin{bmatrix}
cos(θ) & -sin(θ) \\
sin(θ) & cos(θ)
\end{bmatrix}
\begin{bmatrix}
cos(θ) & sin(θ) \\
-sin(θ) & cos(θ)
\end{bmatrix}
=
\begin{bmatrix}
1 & 0 \\
0 & 1
\end{bmatrix}

となることがわかる

また、行列は(というか写像は)演算順序こそ変えられないものの (A ○ B) ○ C と A ○ (B ○ C) は同じ結果になる。

(A ○ B) ○ C とは最初に C(x) で演算した後に、合成された (A ○ B) と演算する
つまり、 (A ○ B)(C(x)) となり、これは最終的に A(B(C(x))) という変換をする意味になる。

次に A ○ (B ○ C) について考えてみよう。
この場合、先にB と Cを合成した (B ○ C) と演算をする。つまりこれは B(C(x)) である。
最後に B(C(x)) を入力値として A を評価する。　つまり A(B(C(x))) である。

したがって (A ○ B) ○ C と A ○ (B ○ C) は全く同じ結果になるのだが、
このような (A ○ B) ○ C と A ○ (B ○ C) が成り立つ関係性を「結合法則が成り立つ」という。
写像の合成は可換ではないが、結合法則であれば成り立つ
試しに先ほど書いた例で見るとTRSの順番さえ保たれていれば演算結果は変わらない

R = rotate_matrix(deg2rad(self.rotation))
S = scale_matrix(self.scale)
T = translate(self.pos[0], self.pos[1])
TRS = np.dot(np.dot(T, R), S)
# TRS = np.dot(T, np.dot(R, S)) と同じ結果になる

以上のような

1. $I(v) = v$ となる $I$ が存在する(この $I$ を写像であれば恒等写像と呼んだりもするし、もっと広く言えば恒等元、単位元とも呼ばれる)
2. $MM^{-1} = I$ となる $M^{-1}$ が存在する (逆元の存在)
3. (A ○ B) ○ C = A ○ (B ○ C) が成り立つ (結合法則の存在)

というような性質を持つ集合が存在する場合、その集合は群である。
(上記の条件は行列ありきで書いてしまったがこれは行列ではなくても、もっと大きな範囲で一般化される)

このような性質は写像の一般的な性質で、この「写像」という概念からその性質を理解することでより行列への理解が深まると思う。
行列の場合は逆写像が存在する行列を正則行列と呼び、この正則行列のみを集めたn次の行列の集合 $GL_n(ℝ)$ という集合が存在するが、これを一般線型群(General Linear Group) と呼ぶ。
$GL_n(ℝ)$ の GL とは General Linear から来ている。

また、逆写像は存在しないケースも存在するので、その場合は群構造にならない点を留意する必要がある。
ちなみに逆写像は全単射じゃないと成立しないので、逆写像が存在しないのであればその写像は全単射ではない

逆関数と逆数

ゲームプログラマに馴染みのある逆関数の例として三角関数の atan, acos, asin がある。
これはそれぞれ アークタンジェント、アークコサイン、アークサインと呼ばれ、tan, cos, sin の逆操作になる。
関数の世界ではこれを「逆関数」と呼ぶが、逆関数は先ほども書いた逆行列と同じ概念である。

それぞれ $atan = tan^{-1}$, $acos = cos^{-1}$, $asin = sin^{-1}$ であるので
$tan^{-1}・tan = cos^{-1}・cos = sin^{-1}・sin = e$ が成り立つ。
(操作と逆操作が打ち消しあってプラマイゼロになるということ)
群論などで写像を要素とする群を扱うとき「恒等写像は操作しないという操作を行う写像である」と考えるのだが、これを数字の1で表現するのは不適切である。
こういったときは群論では度々恒等写像は $e$ と表現しているため、そのように表記している。

cos θ や sin θ が 単位円上で角度θのときのx, y座標 を表しているのであれば acos や asin は 単位円上でのx, y座標を指定すると対応する角度θが手に入る という関係になる。
上記のような式で言えば

1. cos(θ) で角度θのときの x座標が手に入る
2. 角度θのときのx座標をacos に渡すと角度θが手に入る
3. = $cos^{-1}(cos(θ))$ は θ である

といった感じであり、sin, tan も同様である。
このことから、ある2点の点からベクトルを作り、そこから単位ベクトルを計算すればcos, sin, tan が求められるわけである。
(単位ベクトルは長さ1のベクトルであるため、 単位円上のどこかの座標になる。詳しくは 【数学】三角関数の勉強メモ 〜基本の理解〜 に書いているので興味があれば見てみてください)
例えばシューティングゲームで自機狙いの弾を実装したい場合などにこれらの逆関数が重宝する。

ちなみに、セカント(sec) 、コセカント(cosec)、コタンジェント(cot) という関数も存在するが、これはそれぞれ　(cosθ), (sinθ), (tanθ) の逆数であり、$sec = (cosθ)^{-1}$、$cosec = (sinθ)^{-1}$、$cot = (tanθ)^{-1}$であると言える。
逆数と逆関数は名前は似ているものの異なる性質を持っており、 三角関数の逆数 とは $cos(θ)・(cosθ)^{-1} = 1$ となるような値を指す。

逆関数は関数そのものの逆操作で、もしこれらの関数の群が存在していて各関数を 元 とするのであれば、この逆関数は逆元といえる。

逆数はある数と演算すると1になるような数を指すので、この場合は実数の乗法群における逆元であると言える。
どちらも同じように「群」という単位で考えれば役割は同じなのだが、それぞれ操作の対象が異なるのでこのような関係になっている。

写像と関数は何が違う？

写像は最も抽象的に表現された「関数」と考えると良い。
プログラマ的に言えば写像はインターフェースに近く、関数や線型写像はそれを少し具体的にした概念である
よって「関数は写像である」という事はできるが、「写像は関数である」と言うのはあまり適切ではない。
行列に関しては 「行列は線型写像の一種であり、線型写像は写像である」という事はできるが 「写像は行列である」とか「写像は線型写像である」というのも適切ではない

この関係性はアップキャスト/ダウンキャストになんとなく似ている気がする

いろいろ書いていたら長くなってしまったが次は群論について書いてみたい