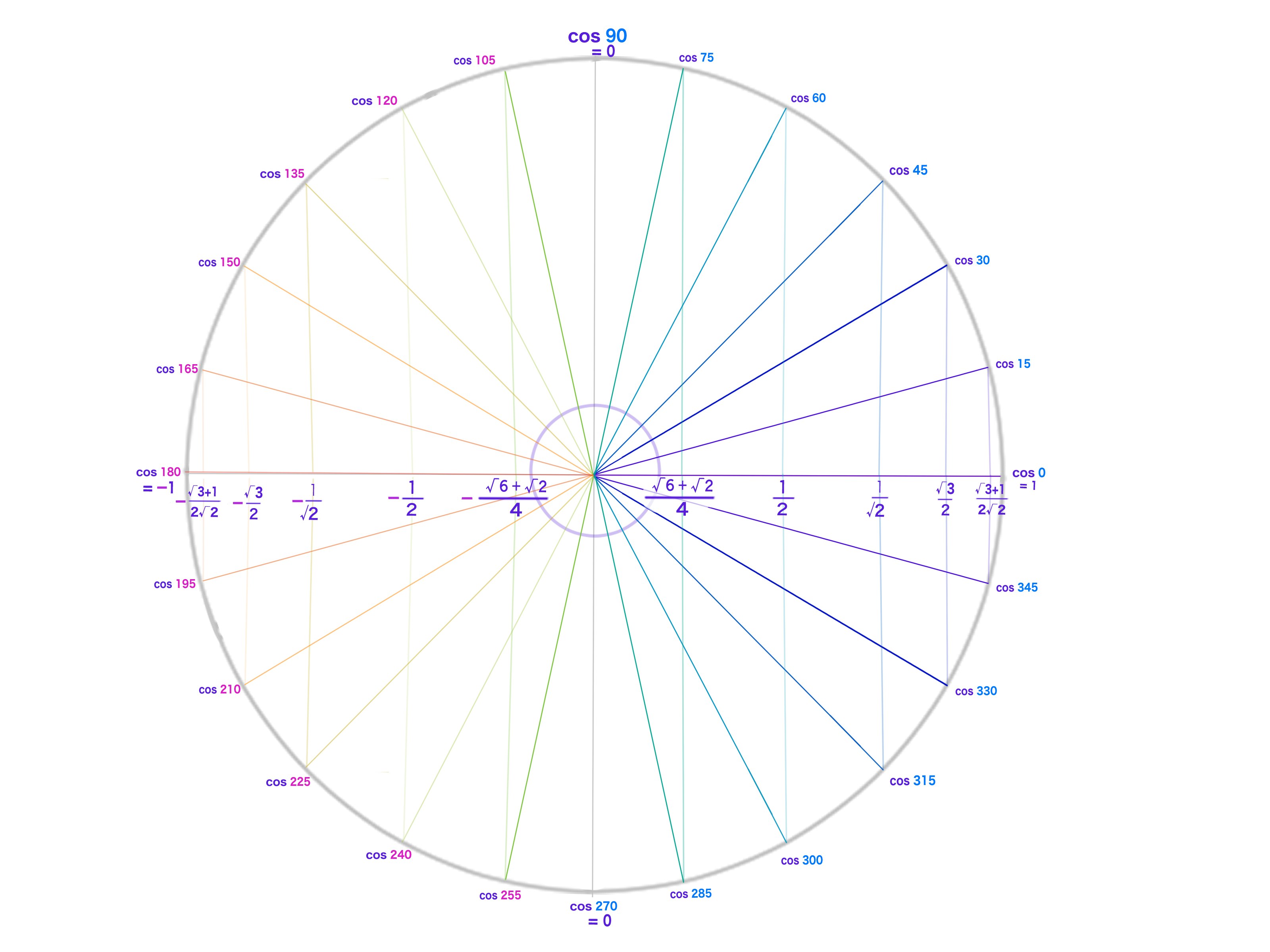
まず最初に三角関数とはなんだろう?という事を考える。
仕事ではよく使う三角関数だが、実際のところこの三角関数というものがどういう性質を持つものなのかあまり考えたことがなかった。
学生の頃に勉強したのだろうけど全く記憶になく、仕事でも「なんか一定の周期で決まった値が返ってくる関数」程度の理解しかなく、今まで雰囲気で使っていたので勉強をし直す事にした。
そのため、この記事は個人的なメモのようなものであり知ってる人からすれば当たり前の話をこれから長々と書くので「何言ってんだコイツ」と思うかもしれないが、そういった人的にはこの記事から得られるものはないと思うので「戻る」を押していただければと思う。
単位円と直角三角形
では、まず最初にこのような円があったと考える。
この円は半径の長さが1の円である。これを 「単位円」 と呼ぶ

この円の曲線上の適当な位置に点を付け、そこと中心位置を結び、さらにx軸と垂直になる線を引く。
するとなんと直角三角形が出来上がる。
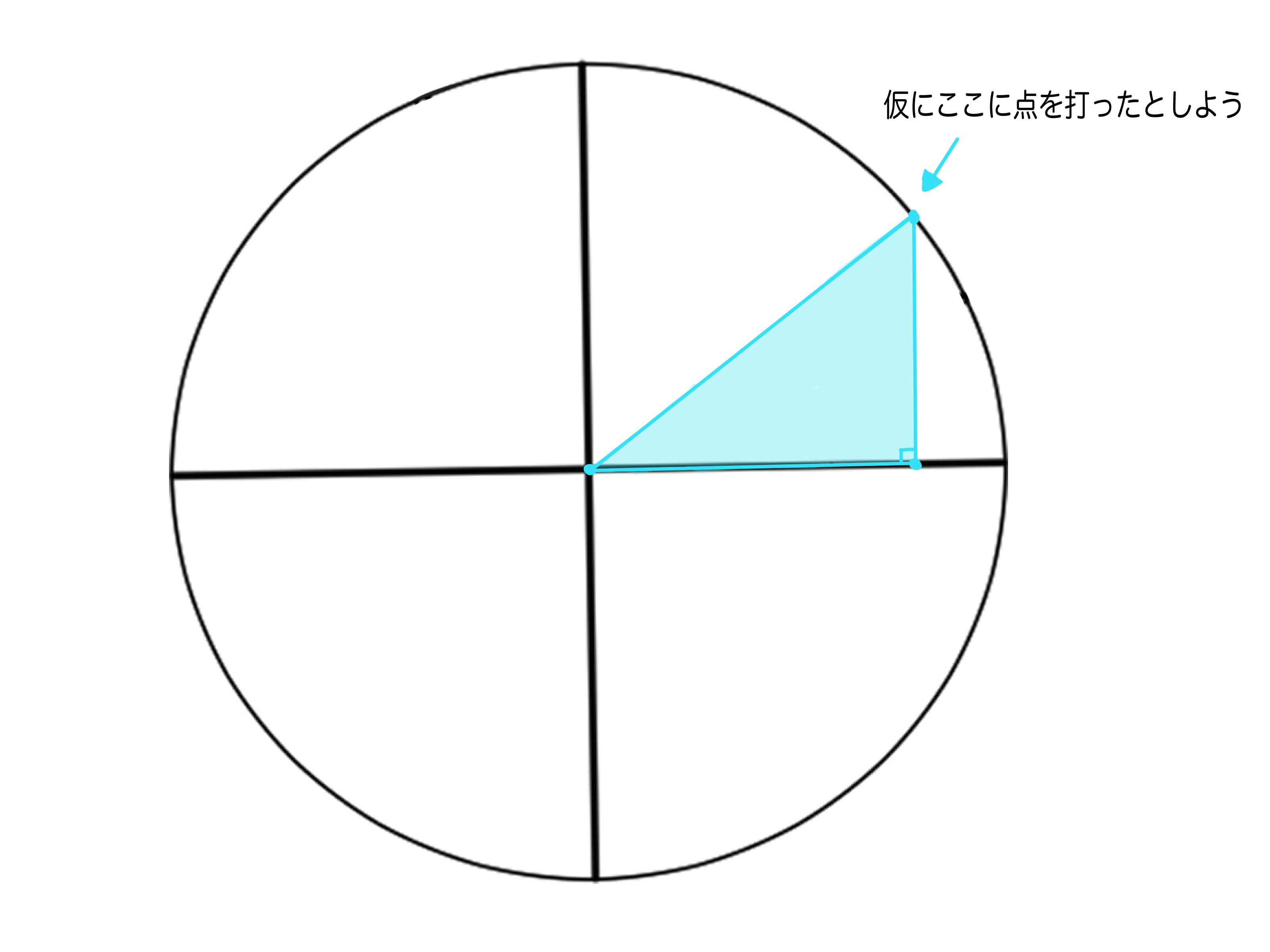
このとき、この点と中心を繋いだ斜めの線を 「斜辺」 と呼ぶ。
斜辺と底辺からなる角度の事をここでは θ(シータ) と呼ぶ事にするが、名前はなんでも良い。
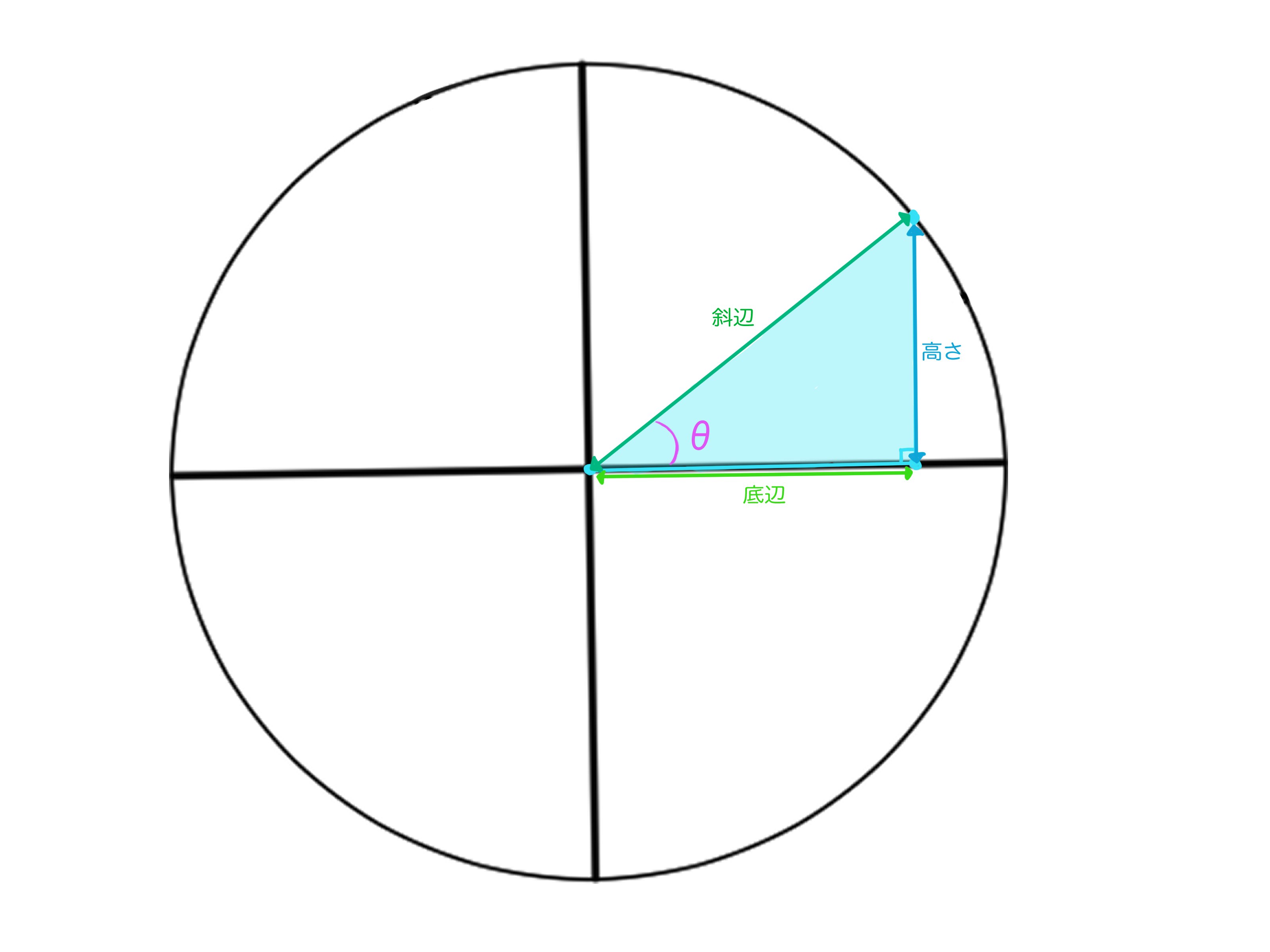
この円の半径は1なのでこの斜辺の長さは当然ながら 1 である。
では、この三角形の底辺と高さはどのような値なのだろうか? と考えたとき、実はこの三角形の底辺と高さは必ず cos(θ) とsin(θ) になる。
その為、この点の座標は (cosθ, sinθ) である。

これは θが どのような値であっても同じであるが、90°を超えると直角三角形にならないので、一旦は90°までの範囲で考えよう。
そして ピタゴラスの定理(もしくは三平方の定理) と呼ばれる定理があり、これによるとどのような直角三角形でも 底辺と高さの2乗 を足した値は斜辺の長さの2乗になる。つまり底辺をa、高さをb、斜辺をcとするなら
$a^2 + b^2 = c^2$
が成立する。
ということはこの単位円上に作られる直角三角形にも以下の性質があることがわかる。
$cos^2 θ + sin^2 θ = 1$
底辺の2乗と高さの2乗を足せば斜辺の2乗になるのだから上図の様な三角形であれば cosθ を2乗したものと sinθ を2乗したものは1の2乗、つまり1になる。
この方程式は非常に有用で半角の公式や2倍角の公式の導出方法を覚えるときや、その他 $cos^2$ や $sin^2$ が方程式に登場した際に役立つ。
もう少し深掘りをしたい。直角三角形は斜辺が長くなればそれに比例して底辺と高さも斜辺の長さ分長くなる。
斜辺の長さをr倍したなら底辺も高さも同じ様にr倍されるのでそれぞれ r cosθ、 r sinθ となる。

では斜辺の長さが2で斜辺と底辺からなる角度が30°の直角三角形の底辺と高さはいくつになるだろう?
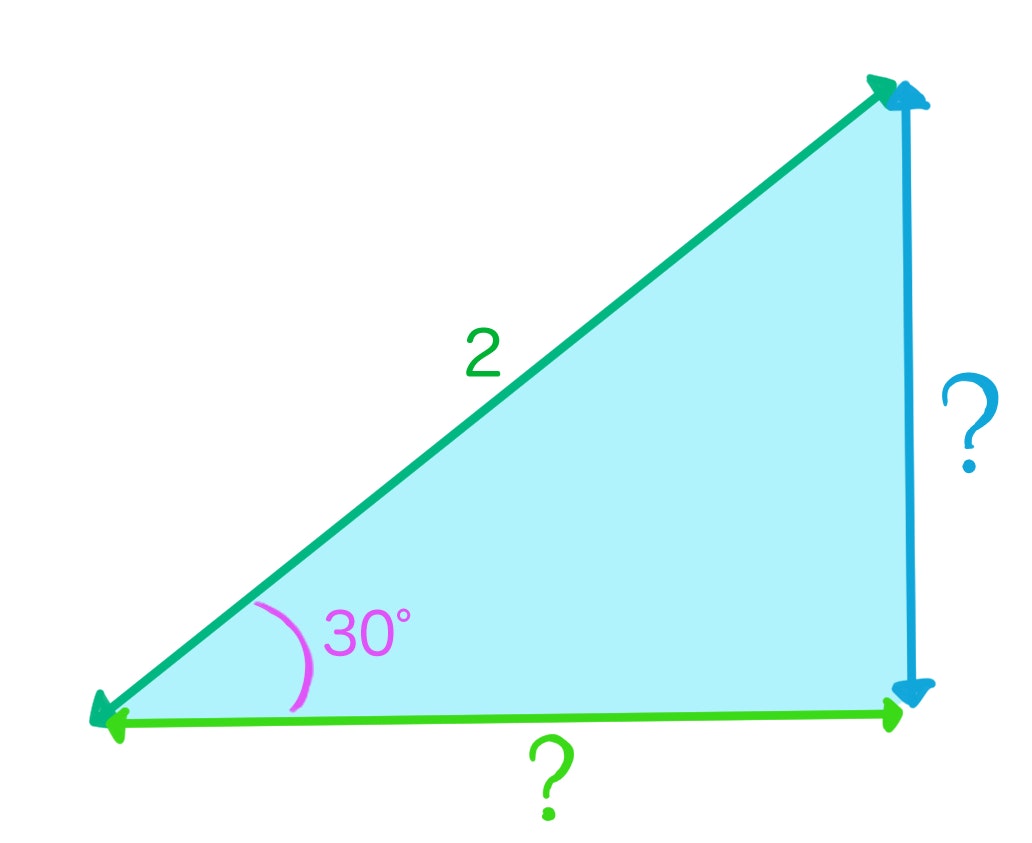
このとき、底辺は $√3$ であり、高さは $1$ である。

これは学生時代、暗記させられた内容の一つだが、これまでの流れから考えるとこれらは $2cos\frac{π}{6}$, $2sin\frac{π}{6}$ といっても問題ない。(面倒なので以降はcos30,sin30と書く)
斜辺の長さに比例して底辺と高さが変わるのだから cosθ と sinθ は斜辺の長さで割れば取得できるはずである。
つまりこの場合2で割れば cos(30)とsin(30)の値がそれぞれ取得できる。
関数電卓などで計算しても cos(30) は $\frac{\sqrt{3}}{2}$ であり、sin(30) は0.5であることがわかる事からもちゃんと2倍されていたという事がわかる。

さて、上述のようにある直角三角形からcosθ、sinθ、tanθなどを求める公式として以下のような式も学生なら一度は暗記させられたはずである。
cos θ = 底辺 / 斜辺
sin θ = 高さ / 斜辺
tan θ = 高さ / 底辺
しかしこれはよく見ると cosθ と sinθ の求め方に関しては単位ベクトルの計算そのものでもある。
例えば、この斜辺を (r cosθ, r sinθ) のベクトルであると考えるなら、このベクトルは長さ r で割れば単位ベクトルになる。
先ほどの角度30°の直角三角形で考えるなら斜辺の長さは三平方の定理に当てはめれば $(\sqrt{3})^2+(1)^2 = 2^2$ になるが、例えばこれを原点(0,0) から ( $2cos30$, $2sin30$) という点を結ぶベクトルと考えてみよう。
二次元ベクトルの大きさは $\sqrt{x^2+y^2}$ で求められるのだから $\sqrt{(2cos30)^2+(2sin30)^2}$
となる。
つまり $\sqrt{4cos^230 + 4sin^230}$
$cos30$ は 約 0.8660254038 であり、これを2回かけると 0.75。つまり $cos^230=0.75$
これを最後に4倍すると3になる。
同じように $sin30$ は 0.5 であり、同じように求めると0.25。つまり $sin^230=0.25$
これを最後に4倍すると1になる。
つまり $\sqrt{4} = 2$ になるので同じように長さを求める事ができた。
単位ベクトルはx, yにそれぞれ長さを割ればいいのだから 2cos30 と 2sin30 はそれぞれ
$\sqrt{3}$ と 1なのだから 2で割れば $\frac{\sqrt{3}}{2}$, 0.5 となるので結果的にcos30°とsin30°を導出する事ができる。
ベクトルを長さ1の単位ベクトルに変換するということは $cos^2 θ + sin^2 θ$ の計算で導ける形になっているという事なので、つまり単位ベクトルのx, yを使って逆三角関数 (arctan, arccos, arcsinなど) の計算をすれば角度を求めることが出来る。
cos と sin 関数
ここまで書いたものはあくまで直角三角形が作れる範囲での話であるため、100°や150°となったときも考慮するならもう少し cos と sin の性質について深掘りする必要がある。
とはいっても基本的には単位円を作り、その円形の座標 (cosθ, sinθ)であるという点は変わらない
cos 関数
cos 関数は単位円の中心点を原点として、その円の右端から反時計回りに単位円上を移動したときの点 x 座標と言える。
右端 (1,0) を始点とし、そこからθ角度移動していく。
θが90°になると中心位置であるため、x座標は0になり、90°を超えると今度はマイナス値になり、180°で-1となる。
180°から270°まで動かすとまた左から中心に戻り、360°になったタイミングで再び1に戻る。
つまり cos はx軸上の 1 ~ -1 の区間を行ったり来たりするものと言える。
sin 関数
sin も cos と同じく、こちらは 円の右端から反時計回りに単位円上を移動したときの点 y 座標と言える。
sin は θが0のとき、0から始まる。そこから上方向に上昇し90°になると1となる。
つまり sin はy軸上の 1 ~ -1 の区間を行ったり来たりするものと言える。
https://cognicull.com/ja/ukjddhq9
このサイトのアニメーションが非常にわかりやすかった。
イメージとしてはこんな感じ。
具体的にどの角度にするとcos, sin, tanの値がどうなるのかはこのサイトが参考になった
三角関数電卓
まずは基本。
余弦定理、加法定理、2倍角の公式、半角の公式、三角関数の微分積分 などを覚える場合は基本を押さえておく必要がある。