【代数学】群論やろうぜ！ 対称群を python で実装しながら群の構造を理解する

前回の記事
【代数学】ゲームプログラマのための代数学 集合と写像

群論を学ぶ際の注意

「群」とは集合の中である演算規則が成り立つときに定義される。
この演算規則は 例えば整数の集合 ℤ において群は 「加法の群」 と 「乗法の群」 が存在する。
加法の群は足し算を定義している群なので ab = c のような式がある場合は、 a + b = c という意味になる。
この辺をごっちゃにして「あれ、なんでこれ成り立つんだ？」と勘違いしてしまうことがあったので備忘録として残しておく

対称群とは？

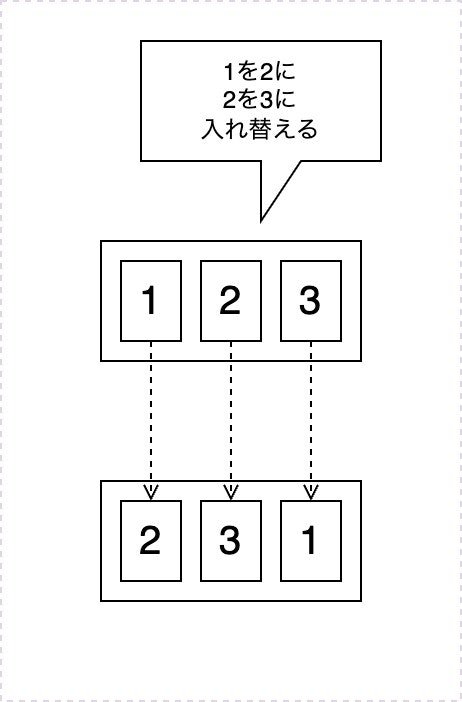
対称群(または置換群とも呼ぶ) とは (1, 2, 3) のような順序付きの集合を「並び替える操作」を要素とする群である。
イメージとしては以下のようになる

このように (1 2 3) の集合を置き換える場合、合計で何パターン存在するだろうか？
答えから書くとこの場合は6パターンである

置き換え後	サイクル表示	サイクル分解
2 1 3	(1 2)
3 2 1	(1 3)
1 3 2	(2 3)
2 3 1	(1 2 3)	(1 2)(2 3)
3 1 2	(1 3 2)	(1 3)(2 3)
1 2 3	()

この置換操作を表すとき、例えば 「1を2に、2を1に」 置換する場合は (1 2) 、
「1を2に、2を3に、3を1に」 置換する場合は (1 2 3) といったように表示される。

この表示を一般的に サイクル と呼ぶ。
また、(1 2) の場合 「長さ２のサイクル」と呼ばれ、(1 2 3)の場合は「長さ3のサイクル」などと呼ばれる。
(1 2 3 4) なども出てくるが、サイクルの長さと言われれた場合同じ要領で考えれば良い。

この長さ3のサイクル、例えば (1 2 3) は (1 2)(2 3) というサイクルの組み合わせで表現できる。
このようなサイクルの組み合わせを 積 と呼び、サイクルの積に分解する事を サイクル分解 と呼ぶ
(この辺りは調べてもサイクルについて既に知っている前提のような資料しか出てこなかったので少し自信がないので、間違ってたら指摘いただけると助かります)

つまりこのように入れ替える

これをサイクルの積に分解するとこのようになる

この操作は前回触れた写像であり、 写像を合成する場合 f ○ g と書き、これは f(g(x)) となるので右から順番に評価される。
よって (1 2)(2 3) と書かれている場合は (2 3) → (1 2) の順番で処理する
また、 () は置換操作が発生しない置換操作である。 () を演算しても集合 (1 2 3) は置換後も (1 2 3) のままである。
このように何もしない写像を 恒等写像 と呼ぶのであった。

また、この置換群は全ての集合に対して作用するので (恒等写像であっても1→1、2→2、3→3とそれぞれ一対一に結びついている)この置換操作は全単射である。

この対称群は Sn と書かれ、 n次の対称群 と呼ばれる。
上記のような (1 2 3) という三つの要素を扱う場合は3次の対称群であり、 S3 と書く。
(1 2 3 4) となった場合は 4次の対称群であり、 S4 と書く

対称群は調べるのが超大変!

この置換操作は合計で n! 個あるので
3次であれば 3 ✖️ 2 ✖️ 1 = 6個
4次であれば 4 ✖️ 3 ✖️ 2 ✖️ 1 = 24個
5次であれば 5 ✖️ 4 ✖️ 3 ✖️ 2 ✖️ 1 = 120個
と、次数が増えるに従って手作業は厳しくなる。
sympy などのライブラリでも対称群は扱えるようなのだが、イマイチ使い方が理解できなかったので自作することにした。

python で対称群を実装する！

というわけでここからが本題
群論を学ぶに辺り、剰余類や共役類や商群などを覚える時、対称群を例に構造を調べつつ覚えることには群論への深い理解を得られると思ったので python で対称群の演算を行う機能を作ることにした。

抽象代数学では群の構造の証明方法も抽象的なので、不慣れな自分はどの証明も何を言ってるのかよくわかっていない。
まずは具体例となる構造を解析しながら最終的にその概念を抽象化できるようにしていく事でこういった証明も理解できるようになるかもしれない。

サイクルの積を構築する

まずはどのように対称群を構築するか？ という点に関して考える。
先ほども書いた通り、対称群とは (1 2 3 ... n) という集合を並べ替える操作の集合であるので、まずは全パターンの並び替え集合を作ることにした。

python の場合、これに関しては itertools の permutations を使うことで簡単に実現できる。

from itertools import permutations

identity_set = (1, 2, 3)
permuted_sets = list(permutations(identity_set))

for set in permuted_sets:
    print(set)

これを実行すると以下のような出力結果を得られる

(1, 2, 3)
(1, 3, 2)
(2, 1, 3)
(2, 3, 1)
(3, 1, 2)
(3, 2, 1)

上記の集合が置換された後の集合一覧となる。
identity_set の値を原点と考え、 permuted_sets のそれぞれが何回の置換操作で identity_set にできるのか？ で逆算を行いサイクルの積を作る。
少し大きめの対称群で考えてみたいので、4次対称群の (1, 2, 3, 4) を (4, 1, 2, 3) に置換する という状況を仮定して考えてみよう

「置換前の集合(以降 identity_set と呼ぶ)」の要素 identity_set[0] = '1' が 「置換後の集合(以降 permuted_set と呼ぶ)」 の何番目の要素に存在するのかを調べる。

この場合、1 番目に '1' が存在する
'1' は permuted_set[0] になければいけないので、permuted_set[0] の値と交換する必要がある。
この場合は 1 と 4 を入れ替える。つまり、(1 4) の置換である

次も同様に identity_set[1]にある '2' の値が permuted_set の何番目に存在するのかを確認する。
permuted_set[2]に存在するので、このpermuted_set[2]と permuted_set[1] の要素を入れ替えるので (2 4) の置換操作となる。

これ以降も同様で、次は現在 3 の値がある場所と permuted_set[2] にある値を入れ替える。

(3 4)(2 4)(1 4) というサイクルの積を求めることが出来た
このアルゴリズムを python で書くと以下のようになった

# permuted_set の値を解析してサイクルの積を求める
def parse_cycle_products(permuted_set: tuple, identity_set: tuple):
    cycles = []
    identity_index = 0
    temp_set = list(permuted_set)
    for value in identity_set:
        permuted_index = temp_set.index(value)
        # インデックスが一致しないのであれば identity_index にある要素と入れ替えを行う
        if permuted_index != identity_index:
            cycles.append([temp_set[permuted_index], temp_set[identity_index]])
            temp_set[permuted_index], temp_set[identity_index] = temp_set[identity_index], temp_set[permuted_index]

        identity_index += 1
    return cycles

サイクルを求める

これだけだとサイクルがわかりづらいので、次にサイクルも同様に求めてみる
これもサイクルの積と同様に identity_set と permuted_set の値で求めてみる。
サイクルは S3 だと出現しないのでわからないが、4次以降は (1 2)(3 4 5) のような形も出現する可能性があるため、

サイクルの求め方は次のように考えてみた。

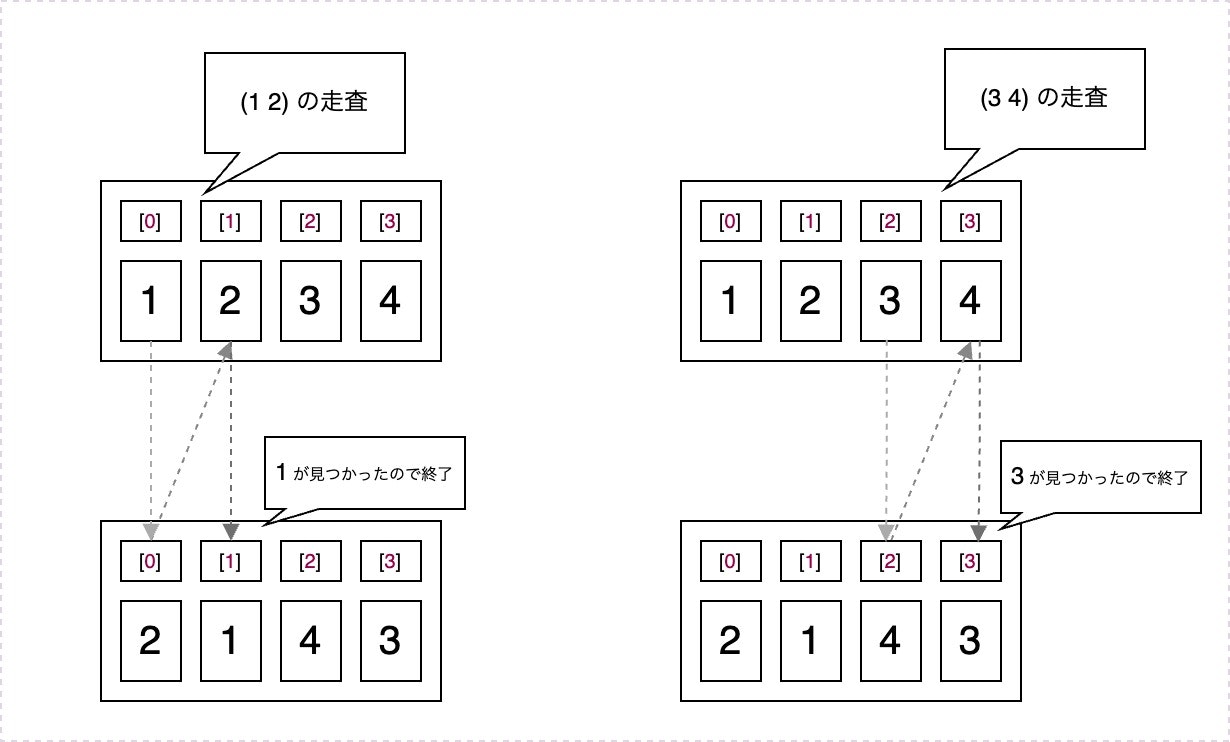
(1,2,3,4) → (4,1,2,3) という順番で置換する場合
1 を スタート地点としてスタート地点が見つかるまで参照先を走査する
この場合1→4→3→2 の順番で走査し、最後に 1が見つかったら一巡したのでそこで終了とする。
この場合、最終的に求まるサイクルは (1 4 3 2) となる。

ただし、 (1 2)(3 4) や (1 3)(2 4)のようなケースがあるので置換パターンを網羅する必要がある
アルゴリズムそのものは上記のものと同じ
走査開始地点が (3 4) であれば 3から開始、 (2 4) なら ２から開始するといった感じで考える。

(1 2)(3 4) の例

一度走査した要素は2回目以降は見る必要がないのでチェック済みであればスキップするようにする必要もある。

これを以下のように実装してみた。

# 置換前 → 置換後のサイクルを求める。
# 例えば identity_set が (1 2 3) で permuted_set が (2 3 1) である場合、
# 1 → 2 → 3 → 1 という置換になるので計算結果は (1 2 3) になる。
# identity_set が (1 2 3 4) で permuted_set が (2 1 4 3) の場合、
# 「1 と 2 の交換」と 「3 と 4 の交換」という操作になる(循環しないので別々の操作と扱う) ので
# (1 2)(3 4) となる
def scan_cycle(identity_set: tuple, permuted_set: tuple) -> tuple[tuple]:
    cycle_value: list[tuple] = []

    def has_scanned(value):
        for cycle in cycle_value:
            if value in cycle:
                return True
        return False

    # value が identity_set の何番目に存在するのかをチェックし、 identity_set にセットされている場所の permuted_set の値をチェックする。
    # 走査済みではないのであれば cycle に perm_value を登録し、今度は perm_value の値を使って再帰的に同様のチェックを行う。
    def find_cycle(value, cycle: list[int]):
        id_index = identity_set.index(value)
        perm_value = permuted_set[id_index]
        if perm_value in cycle or has_scanned(perm_value):
            return
        cycle.append(perm_value)
        find_cycle(perm_value, cycle)

    for index in range(len(identity_set)):
        id_value = identity_set[index]
        if has_scanned(id_value):
            continue
        perm_value = permuted_set[index]
        if id_value != perm_value:
            cycle = [id_value, perm_value]
            find_cycle(perm_value, cycle)
            cycle_value.append(tuple(cycle))

    if len(cycle_value) == 0:
        cycle_value.append(tuple([]))
    return tuple(cycle_value)

群と要素の関係性を持ったクラスを作る

これらのサイクルの積とサイクルを持った対称群の要素を表すクラスとして PermutationGroupElement というクラスを定義する

# 対称群の元を定義する
class PermutationGroupElement:
    # identity_set ... 恒等元の役割を持つ、 (1,2,3,...n) の集合
    #              この値をもとに置換操作を行う
    # permuted_set ... identity_set を置換した後の数列
    def __init__(self, identity_set: tuple, permuted_set: tuple) -> None:
        self.identity_set = identity_set
        self.permuted_set = permuted_set
        self.permutations = parse_cycle_products(self.permuted_set, identity_set)
        self.cycle_value = scan_cycle(self.identity_set, self.permuted_set)

この PermutationGroupElement は群の要素でなければいけないので
要素を管理する群クラスを用意する。
剰余類や共役類、商群や巡回群などの存在を考慮すると「対称群だけ」ではなく置換操作によって作られた群全般を表現できたほうが良い。
名前は「置換群」というより広い意味合いを含めるために PermutationGroup という名前にする。

class PermutationGroup:
    def __init__(self) -> None:
        self.root: PermutationGroup = None
        self.identity_set: tuple[int, ...] = ()
        self.elements: dict[tuple, PermutationGroupElement] = {}

しかし、対称群は交代群 An なども含めたいので対称群は対称群で別途クラスが欲しいので、SymmetricGroupという名前で継承して実装することにした

class SymmetricGroup(PermutationGroup):
    # 次数 n の順序付き集合を作る
    # 例として n が 3 の場合は (1, 2, 3) という集合になる。
    def __init__(self, n: int) -> None:
        super().__init__()
        identity_set = []
        for i in range(n):
            identity_set.append(i + 1)
        self.root = self
        self.identity_set = tuple(identity_set)

        # 全ての組み合わせパターンを生成
        permuted_sets = list(permutations(self.identity_set))
        for permuted_set in permuted_sets:
            element = PermutationGroupElement(self, self.identity_set, permuted_set)
            self.elements[element.id] = element

実際はもう少しいろいろと書いているのだが、本記事には不要と判断し割愛している。
今回は数学的な話を中心にしたいのであまり技術的な部分には触れないが、実際のソースコードは以下の GitHub リポジトリに上げているので興味のある方は見て頂ければと
https://github.com/kawawa1989/py-algebra

商群を求める

以上のような流れを経て置換群をプログラムした。
さっそくこの置換群を使い群の構造について調べてみたい。
今回は ４次対称群 S4 を作成してその構造を調べてみようと思う

そもそも商群とか剰余類って何よ？という方もいるかと思うので説明したいものの、これは実際に計算した結果を出しながら解説したほうがわかりやすいと思うので実行結果を見ながら解説していく

交代群を求める

まず、群を G という名前で仮定したとき その正規部分群 H が存在するのであればその二つの商群 G/H を作ることができる。
というのが商群の定義である。
次に「正規部分群ってなに？」という話になるのだが、一旦は 「ある群の中に存在するもう一つの群」 くらいの認識で良い。

対称群には必ず正規部分群が存在するという面白い性質がある。
それは交代群 An と呼ばれる群で、対称群 S4 の場合は交代群の次数も4で A4 という名前になる。
今回作ったプログラムでも交代群は求められるので早速求めてみよう

まず S4 の要素は以下の通りになる

S4 = SymmetricGroup(4)
print("-------------------------------")
print(f"S4 (length={S4.order}):")
print("-------------------------------")
print(S4)

実行結果
-------------------------------
S4 (length=24):
-------------------------------
()
(3, 4)
(2, 3)
(2, 3, 4)
(2, 4, 3)
(2, 4)
(1, 2)
(1, 2)(3, 4)
(1, 2, 3)
(1, 2, 3, 4)
(1, 2, 4, 3)
(1, 2, 4)
(1, 3, 2)
(1, 3, 4, 2)
(1, 3)
(1, 3, 4)
(1, 3)(2, 4)
(1, 3, 2, 4)
(1, 4, 3, 2)
(1, 4, 2)
(1, 4, 3)
(1, 4)
(1, 4, 2, 3)
(1, 4)(2, 3)

次に交代群を見てみよう
SymmetricGroup に alternating_group という交代群を取得するプロパティを追加した。

A4 = S4.alternating_group
print("-------------------------------")
print(f"A4 (length={A4.order}):")
print("-------------------------------")
print(A4)

実行結果
-------------------------------
A4 (length=12):
-------------------------------
()
(2, 3, 4)
(2, 4, 3)
(1, 2)(3, 4)
(1, 2, 3)
(1, 2, 4)
(1, 3, 2)
(1, 3, 4)
(1, 3)(2, 4)
(1, 4, 2)
(1, 4, 3)
(1, 4)(2, 3)

交代群の性質

交代群の要素数は常に対称群の要素数の半分であり、
例えば $S_3$ なら　$S_3$ は6つあるので $A_3$ は要素数が 3 つとなるし、
$S_4$ の交代群 $A_4$ であれば 24個の半分なので 12 個、
$S_5$ であれば120個あるので $A_5$ は 60個となる。

ではどのような要素が交代群の要素になるのか？
長さ 2 のサイクルまで分解したときにサイクル数が偶数になる場合、それを 偶置換 と呼ぶ。(逆に奇数なら 奇置換 と呼ぶ)

交代群はこの偶置換の集合である。
では実際にどのようなサイクル数になるのか、サイクルの積を見てみよう。

先ほど求めたサイクルの積は各要素に持たせているので、この積を使って一覧表を作ってみる。

置換後の集合	サイクル	サイクルの長さ	サイクルの積
(1,2,3,4)	()	0	()
(1,3,4,2)	(2 3 4)	2	(2 3) (3 4)
(1,4,2,3)	(2 4 3)	2	(2 4) (3 4)
(2,1,4,3)	(1 2)(3 4)	2	(1 2) (3 4)
(2,3,1,4)	(1 2 3)	2	(1 2) (2 3)
(2,4,3,1)	(1 2 4)	2	(1 2) (2 4)
(3,1,2,4)	(1 3 2)	2	(1 3) (2 3)
(3,2,4,1)	(1 3 4)	2	(1 3) (3 4)
(3,4,1,2)	(1 3)(2 4)	2	(1 3) (2 4)
(4,1,3,2)	(1 4 2)	2	(1 4) (2 4)
(4,2,1,3)	(1 4 3)	2	(1 4) (3 4)
(4,3,2,1)	(1 4)(2 3)	2	(1 4) (2 3)

となるので 全て偶数回数であることがわかった。

交代群は正規部分群

交代群は正規部分群である。
やや順不同になるのだが、次は「部分群とは何か？」についてを $S_4$ 、$A_4$ を用いて考えてみよう。

部分群の定義

まず、ある群 $G$ と部分群 $H$ には以下の性質がある。

1. 演算が $H$ において閉じていること
   この「閉じている」　という表現は代数学でしばしば登場するが、つまり $H$ のいかなる要素 $a,b$ を組み合わせ $ab$ という演算を行なってもその演算結果の値もまた $H$ の要素である事を「閉じている」という。
   つまり $ab∈H$ である。

2. $H$ の任意の要素 $a$ についても逆元が $H$ の中に存在すること
   $H$ のどのような要素 $a$ をとってもその $a$ には逆元 $a^{−1}$ が存在し、なおかつ $a∈H$ である必要がある。

3. 部分群 $H$ の単位元は群 $G$ と同じ単位元であること
   単位元とは $ae=a$ となるような $e$ のことを言うのだった。
   この単位元とは恒等写像のことであり、対称群に関して言えば () (置換操作をしない要素) が恒等写像になる。

この3つを満たせば部分群である。
では、部分群を満たしているかを一つ一つ見てみよう。
csv 出力してエクセルで演算表を作ってみた

黄色に塗りつぶされている箇所が部分群 $A_4$ である。

各要素に逆元が存在している
また、全ての演算で $H$ で閉じている事も演算表からわかる
また単位元が存在し、これは $G$ (ここでは $S_4$ のこと) と同一である
というところから $A_4$ は少なくとも部分群ではありそうであることがわかった。

上記のような図でいちいち調べずとも、交代群 $A_n$ は偶置換のみを集めた集合なので、偶置換と偶置換を演算すればその結果も偶置換となる事からその演算は「閉じている」と言える。

置換操作は逆順に積めば逆元となるので逆操作となる偶置換もまた交代群 $A_n$ の中に存在する事がわかる。
例えば (1, 2, 3, 4) を (2, 4, 3, 1) に置換する (1 2 4) という操作は、
まず (2 4) で置き換えをして (1,4,3,2)
次に (1 2) で置き換えをして (2,4,3,1)
という順番で置き換え出来るので、ひっくり返して (2 4)(1 2) という操作 (1 4 2) が逆操作になる。
この事から中身を調べなくても $A_n$ が部分群である事が示せた

共役類(きょうやくるい)の存在

部分群を示せたのは良いが、どうあれば正規部分群なのか？という話が次に来る。
正規部分群は部分群である上で、それに加え 共役類の和 である必要がある。

共役類とは何ぞ？という話になるのだが、これをやる前に同値関係の話が必要になる。
同値関係に関しては後述、一旦群の中には「群には共役類と呼ばれる、ある共通した性質を持つグループで分けることができる」 程度の理解で問題ないと思うのでそのような認識で読んでいただければと思う。

共役類とは、ある群 G の中で全ての要素 a に対して $b = gag^{-1}$ となる b が存在することをいう。
$S_4$ は大きすぎるので対称群 $S_3$ の共役類について考えてみよう。
対称群 $S_3$ の要素とその逆元は以下のように対応付けられる。

$g$	$g^{-1}$
()	()
(2 3)	(2 3)
(1 2)	(1 2)
(1 3)	(1 3)
(1 2 3)	(1 3 2)
(1 3 2)	(1 2 3)

(1 2), (1 3), (2 3) の共役

これに上記の式を当てはめる。

(2 3)

例えば、 (2 3) を aとするなら以下のような演算を全ての要素に対して行う

$g$	$a$	$g^{-1}$		$b$
()	(2 3)	()	=	(2 3)
(2 3)	(2 3)	(2 3)	=	(2 3)
(1 2)	(2 3)	(1 2)	=	(1 3)
(1 3)	(2 3)	(1 3)	=	(1 3)
(1 2 3)	(2 3)	(1 3 2)	=	(1 2)
(1 3 2)	(2 3)	(1 2 3)	=	(1 2)

python では以下のように書くと求められる

S3 = SymmetricGroup(3)
a = S3["(2 3)"]
for g in S3:
    b = g * a * g.inverse()
    print(b)

実はこのとき、(2 3) だけでなく上記の式の $a$ として (2 3), (1 2), (1 3) を指定すれば、結果は必ず (2 3), (1 2), (1 3) のどれかになる。

(1 3)

$g$	$a$	$g^{-1}$		$b$
()	(1 3)	()	=	(1 3)
(2 3)	(1 3)	(2 3)	=	(1 2)
(1 2)	(1 3)	(1 2)	=	(2 3)
(1 3)	(1 3)	(1 3)	=	(1 3)
(1 2 3)	(1 3)	(1 3 2)	=	(1 2)
(1 3 2)	(1 3)	(1 2 3)	=	(2 3)

(1 2)

$g$	$a$	$g^{-1}$		$b$
()	(1 2)	()	=	(1 2)
(2 3)	(1 2)	(2 3)	=	(1 3)
(1 2)	(1 2)	(1 2)	=	(1 2)
(1 3)	(1 2)	(1 3)	=	(2 3)
(1 2 3)	(1 2)	(1 3 2)	=	(2 3)
(1 3 2)	(1 2)	(1 2 3)	=	(1 3)

これは対称群 $S_4$, $S_5$ と増やしても同じ性質を持ったグループが生まれる。
このような関係性を 共役類 と呼ぶわけである。
この共役類は多くの性質を共有している。

() の共役

また、この $a$ を恒等写像にした場合は実質 $gg^{-1}$ と等価なので、全て恒等写像になることがわかる

$g$	$a$	$g^{-1}$		$b$
()	()	()	=	()
(2 3)	()	(2 3)	=	()
(1 2)	()	(1 2)	=	()
(1 3)	()	(1 3)	=	()
(1 2 3)	()	(1 3 2)	=	()
(1 3 2)	()	(1 2 3)	=	()

(1 2 3), (1 3 2) の共役

(1 2 3)

$g$	$a$	$g^{-1}$		$b$
()	(1 2 3)	()	=	(1 2 3)
(2 3)	(1 2 3)	(2 3)	=	(1 3 2)
(1 2)	(1 2 3)	(1 2)	=	(1 3 2)
(1 3)	(1 2 3)	(1 3)	=	(1 3 2)
(1 2 3)	(1 2 3)	(1 3 2)	=	(1 2 3)
(1 3 2)	(1 2 3)	(1 2 3)	=	(1 2 2)

(1 3 2)

$g$	$a$	$g^{-1}$		$b$
()	(1 2 3)	()	=	(1 3 2)
(2 3)	(1 2 3)	(2 3)	=	(1 2 3)
(1 2)	(1 2 3)	(1 2)	=	(1 2 3)
(1 3)	(1 2 3)	(1 3)	=	(1 2 3)
(1 2 3)	(1 2 3)	(1 3 2)	=	(1 3 2)
(1 3 2)	(1 2 3)	(1 2 3)	=	(1 3 2)

共役類は同値関係

共役類は同値関係であり、以下のような関係性が成り立つ。

1. a ∼ a (反射律)
2. a ∼ b (対称律)
3. a ∼ b かつ b ∼ c なら a ∼ c (推移律)

共役類が同値関係であることの検証

∼ は 二項関係 と呼ばれ、書物によっては aRa, aRb のように R で表現することもある。

1. 任意の要素 a を取ってきて $a=eae^{-1}$
   上記の一覧を見ても成り立っていることがわかる。

2. 要素 a, b があるとき $a=pbp^{-1}$
   右から $p$ を演算すると $ap=pb$
   左から $p^{-1}$ を演算すると$p^{-1}ap = b$
   
   このとき、 $q = p^{-1}, q^{-1} = p$ とするなら $qaq^{-1} = b$ なので対称律も成り立っている。
   試しに a = (1 2), b = (2 3), p=(1 3 2) として見てみると
   $a = pbp^{-1}$ は (1 2) = (1 3 2)(2 3)(1 2 3) となる。
   これを上の演算と同じように、両辺に掛け算すると
   (1 2 3)(1 2)(1 3 2) = (2 3) になることもわかる。

3. $①: b = pap^{-1}, ②: c = qbq^{-1}$
   となる p と q がそれぞれ存在するなら、対称律から $c = q(pap^{-1})q^{-1}$ であり、
   $(qp) a (p^{-1}q^{-1})$ になる。
   $qp・p^{-1}q^{-1}$ をするとこれは $q$ $p・p^{-1}$ $q^{-1}$
   $p・p^{-1}$ は単位元 $e$ になるので $qeq^{-1}$ したがって $qq^{-1}$
   $qq^{-1}$ すると e なので $(p^{-1}q^{-1}) = (qp)^{-1}$ となる。
   したがって $c = (qp)a(qp)^{-1}$ が成立するので推移律も成り立つ

少し長くなったので続きはまた別の記事に書きます

参考

対称群の共役類と整数の分割について(プログラミングと仕事論)
部分群とその具体例(高校数学の美しい物語)