1. はじめに
1-1. 本記事の概要と目標
今回の分析のテーマは 「電力需要予測」 ということで、
東京電力が公開している実際の電力消費量のデータをもとに、
将来の電力需要を予測するモデルを構築します。
また電力消費量のデータに加えて、
気象庁の公開する天気情報のデータも使用します。
モデルは RNN/GRU/LSTM の3つを使用し、
いくつかの点で精度を比較していきます。
1-2. 分析の流れ
本分析は以下の流れで進行していきます。
1.データの準備
2.データ前処理
3.特徴量作成
4.学習用データの作成
5.モデル構築/学習
6.精度の比較
7.考察
2. RNN/GRU/LSTMの仕組み
2-1. RNN(Recurrent Neural Network)
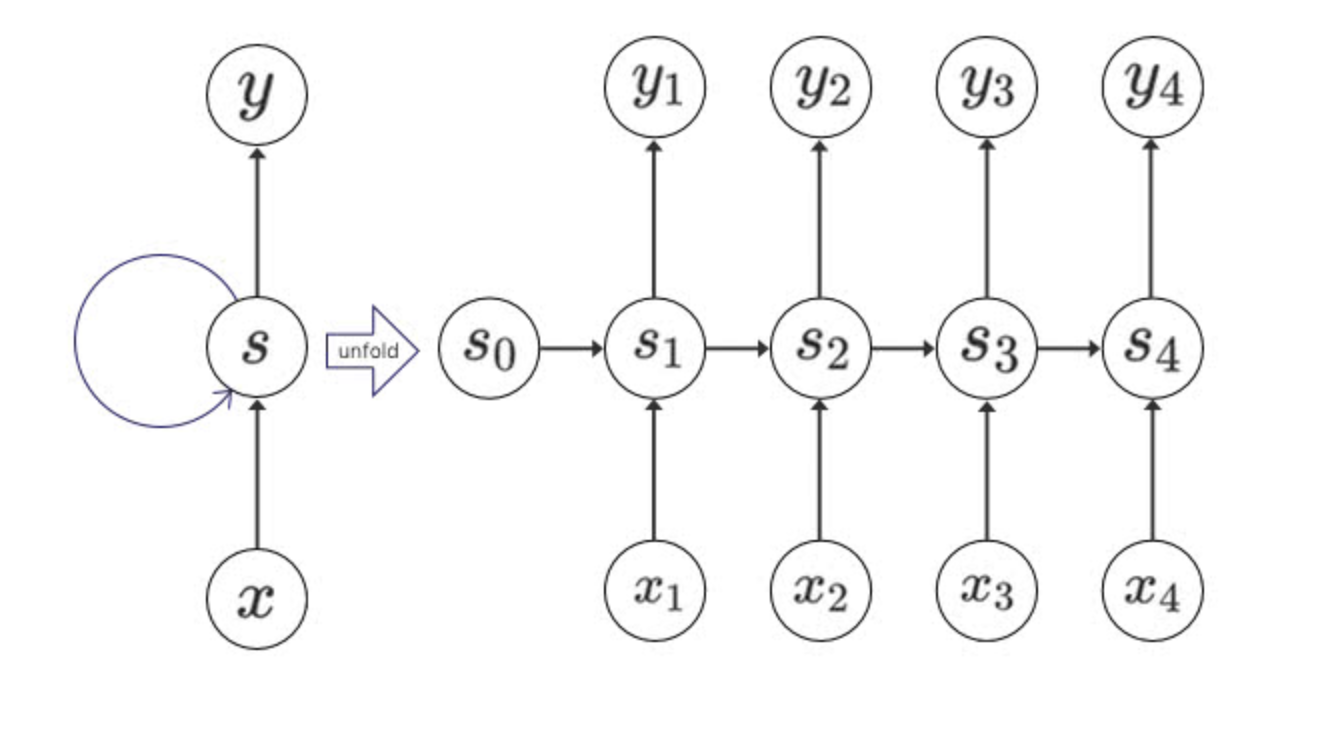
RNNは出力した値を再度入力として用いる、
内部にループ構造を持ったネットワーク のモデルです。
今度こそわかるぞRNN, LSTM編
https://qiita.com/kazukiii/items/df809d6cd5d7d1f57be3
前の出力を次の入力として連続で扱うため、
時系列データや自然言語データなどの、
順序自体に意味を持つデータの学習において力を発揮します。
しかしパラメータの更新の際に勾配消失/勾配爆発が起きやすく、
より長期間のデータになると学習が進まなくなる欠点があります。
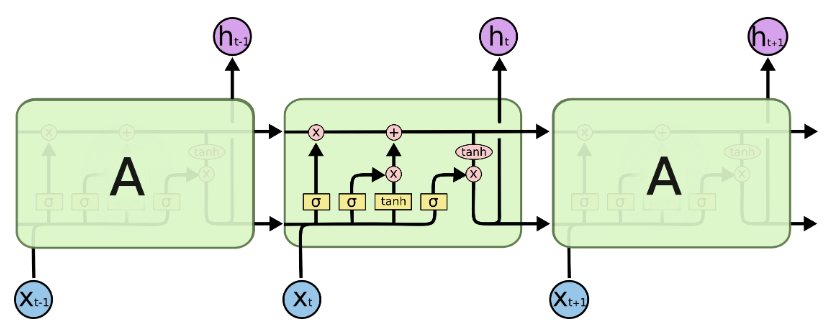
2-2. LSTM(Long Short-Term Memory)
RNNの欠点である勾配消失/勾配爆発に対して、
内部に3つのゲートを持つ ことで改善を図ったのがLSTMです。
今度こそわかるぞRNN, LSTM編
https://qiita.com/kazukiii/items/df809d6cd5d7d1f57be3
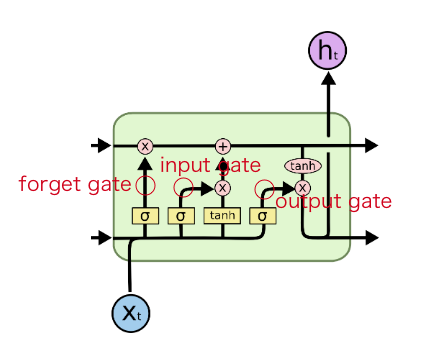
それぞれ3つのゲートは以下の役割を持っています。
・Input gate: セルにエンコードされる新しい情報を制御
・Forget gate: セル内のどの情報を忘れるかを制御
・Output gate: セル内のどの程度情報を次の時刻に伝えるかを制御
今度こそわかるぞRNN, LSTM編
https://qiita.com/kazukiii/items/df809d6cd5d7d1f57be3
RNNと違うのは、内部に値を保持するための構造(セル)を持ち、
長期間に渡って必要な値を保ちながら計算を行える点です。
しかし計算するパラメータが大幅に増えており、
計算コストが高くなっている点が欠点と言えます。
2-3. GRU(Gated Recurrent Unit)
長期で記憶を維持できるという LSTMの長所を持ちながら、
計算をより簡易的に改善 したモデルがGRUです。
GRU(Gated Recurrent Unit)
https://cvml-expertguide.net/terms/dl/rnn/gru/
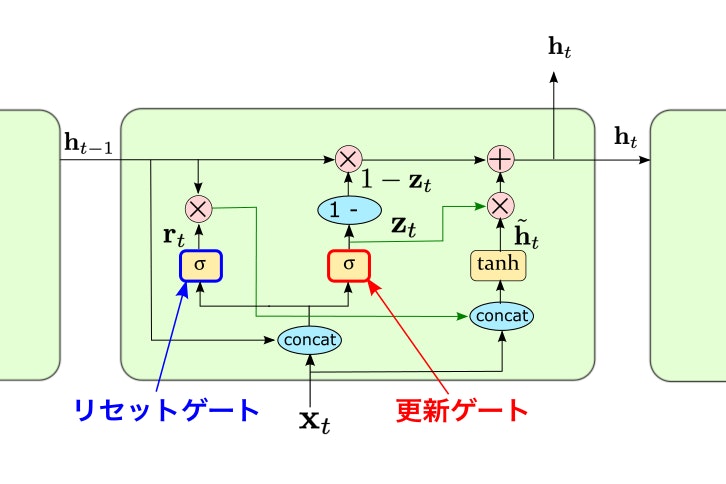
GRUは以下の2つのゲートを内部に持ちます。
・Reset gate: 記憶の忘れる程度を調整
・Update gate: 新たに記憶として覚える程度を調整
上記2つのゲートで計算した重みを用いることで、
入力X_tとh_t-1から次の時刻に渡すh_tを更新しています。
しかし簡易版ということもあって、
長期記憶の機能に関してはLSTMが優れている点は注意です。
2-4. GRUとLSTMの使い分け
入力する特徴ベクトルが低~中次元であり、
系列長もあまり長くない場合にはLSTM で問題はなく、
計算コストが高くなる場合にはGRUが望ましい とされているようです。
今回使用するデータセットは特徴量が10以下で、
系列長は30,000程のデータではありますが、
比較検討が目的であるため全てのモデルを実装します。
3. データの準備
3-1. データのダウンロード
まずは今回の分析のターゲットとなるデータの準備です。
今回の分析では 2018-2021年の4年分 の実績データを使用します。
以下のリンクから取得することが可能です。
data_18 = pd.read_csv("./data/power_demand/juyo-2018.csv", encoding="SHIFT-JIS", skiprows=2)
data_18
実際に読み込んだ2018年のデータの中身を見ると、
2018年の1月1日の0時から1時間ごとに、
電力の消費実績が記録されていることが確認できます。
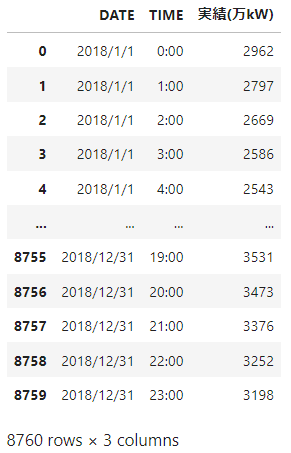
残りのデータも読み込み、日時のデータを少しいじります。
作成するのは 月、日、時間、曜日の特徴量 です。
ついでにカラムの名前も見やすいように変更します。
#2019年以降のデータ読み込みは省略
data = pd.concat([data_18, data_19, data_20, data_21])
data.reset_index(drop=True, inplace=True)
data.rename(columns={"実績(万kW)":"kw"}, inplace=True)
tmp_list = []
for date,time in zip(data["DATE"], data["TIME"]):
strdate = date + " " + time
tmp_list.append(dt.datetime.strptime(strdate, "%Y/%m/%d %H:%M"))
data["datetime"] = tmp_list
data["month"] = data["DATE"].map(lambda x : x.split("/")[1])
data["day"] = data["DATE"].map(lambda x : x.split("/")[-1])
data["hour"] = data["TIME"].map(lambda x : x.split(":")[0])
data["weekday"] = data["datetime"].map(lambda x : dt.datetime.weekday(x))
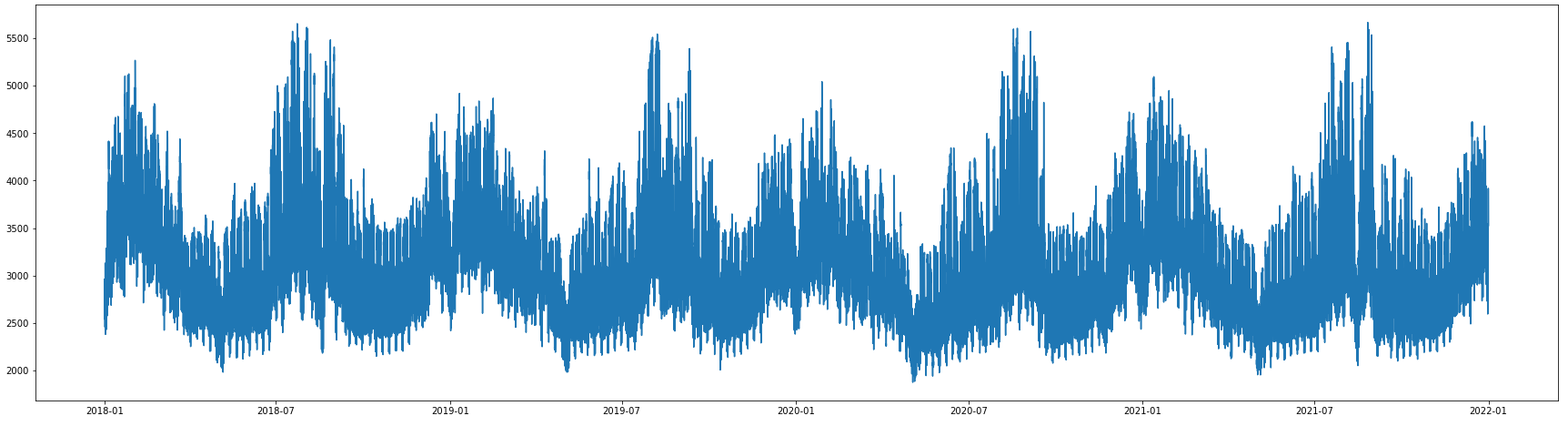
ここで取り込んだ電気使用量のデータを見てみると、
夏と冬の時期にそれぞれ増加している様子が分かります。
plt.figure(figsize=(30,8))
plt.plot(data["datetime"], data["kw"])
plt.show()
次に気象庁の公開する天気情報から、
同期間における 「天気, 降水量, 気温, 湿度」 のデータを取得します。
こちらのサイトでは同時取得可能なデータ数が限られているので、
必要なデータを少しずつ取得し、後でCSVデータを結合して使用します。
weather_18_0 = pd.read_csv("./data/weather/tokyo_2018/with_temperature.csv", encoding="SHIFT-JIS", skiprows=3).iloc[1:,:2]
weather_18_1 = pd.read_csv("./data/weather/tokyo_2018/with_precipitation.csv", encoding="SHIFT-JIS", skiprows=3).iloc[1:,:2]
weather_18_2 = pd.read_csv("./data/weather/tokyo_2018/with_weather.csv", encoding="SHIFT-JIS", skiprows=3).iloc[1:,:2]
weather_18_3 = pd.read_csv("./data/weather/tokyo_2018/with_humidity.csv", encoding="SHIFT-JIS", skiprows=1).iloc[2:,:2]
weather_18_3.rename(columns={"Unnamed: 0":"年月日時", "東京":"湿度"}, inplace=True)
weather_18_3.reset_index(drop=True, inplace=True)
data18 = weather_18_0.join([weather_18_1.iloc[:, 1], weather_18_2.iloc[:, 1], weather_18_3.iloc[:, 1]])
取得した項目によってCSVの作りが違うので、
with_humidityのデータだけskiprowsの数を変えています。
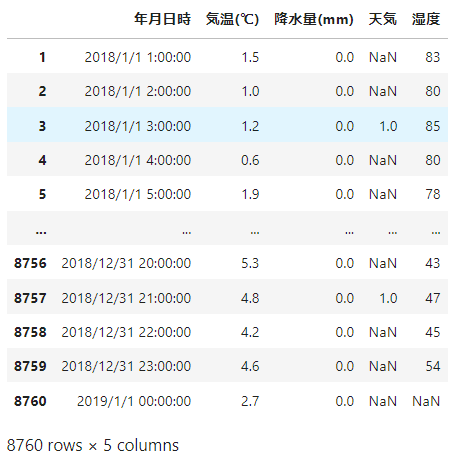
見やすいようにカラムの名前を変更し、
取得した2018年の天気情報を見ると画像のようになります。
ここでの注意点は以下の3つです。
・取得日時が1/1の1時からになっている
・天気記号に対応した番号が振られている
・天気が3時間置きでしか観測されていない
残りのデータも同様に読み込み、縦に結合します。
また天気情報はその日の中で近い時間の天気を複製し、
日時の表示形式を電気使用量のデータに合わせます。
#2019年以降のデータ読み込みは省略
weather_data = pd.concat([data18, data19, data20, data21])
weather_data.reset_index(drop=True, inplace=True)
start_num = 0
weather_list = []
for _ in range(int(weather_data.shape[0]/24)):
tmp_df = weather_data.iloc[start_num: start_num+24, 3]
tmp_df.reset_index(drop=True, inplace=True)
for _ in range(4):
weather_list.append(tmp_df[2])
for _ in range(3):
weather_list.append(tmp_df[5])
for _ in range(3):
weather_list.append(tmp_df[8])
for _ in range(3):
weather_list.append(tmp_df[11])
for _ in range(3):
weather_list.append(tmp_df[14])
for _ in range(3):
weather_list.append(tmp_df[17])
for _ in range(5):
weather_list.append(tmp_df[20])
start_num += 24
weather_data["天気"] = weather_list
weather_data["年月日時"] = weather_data["年月日時"].map(lambda x : dt.datetime.strptime(x, "%Y/%m/%d %H:%M:%S"))
weather_data.rename(columns={"年月日時":"datetime"}, inplace=True)
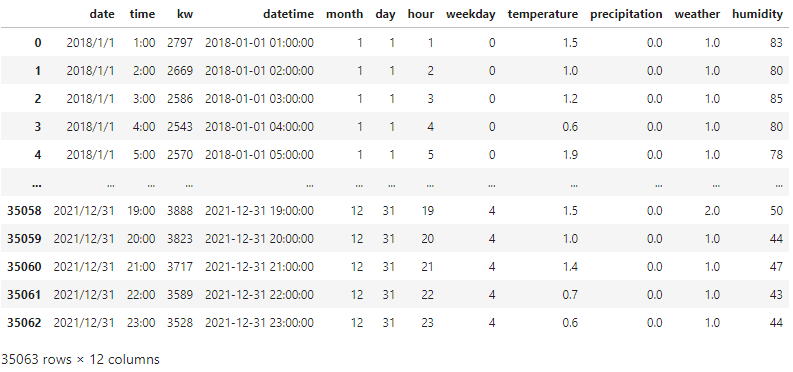
ここで電気使用量のデータと天気情報のデータを結合します。
改めてカラムをここで整理しておきます。
df = pd.merge(data, weather_data, how="left", on="datetime")
# 2019/01/01 00:00(0行目)の天気情報データが無かったので削除
df = df.iloc[1:, :].reset_index(drop=True)
df.rename(columns={"DATE":"date", "TIME":"time", "気温(℃)":"temperature", "降水量(mm)":"precipitation", "天気":"weather", "湿度":"humidity"}, inplace=True)
3-2. 前処理
改めてここからデータの前処理を行います。
まずは天気の情報が特殊な値になっているので、
こちらのページを参考に直していきます。
変換のイメージとしては以下の通りです。
0.0:「晴れや快晴」外出の妨げにならない気候状態
0.5:「曇りや霧」若干外出の妨げになる気候状態
1.0:「雨や雷」外出の妨げになる気候状態
上記のイメージで各天気を主観的に数値化しています。
#天気一覧から辞書を作成
w_dic = {1:0.0, 2:0.0, 3:0.3, 4:0.5, 5:0.6, 6:1.0, 7:1.0, 8:0.6, 9:0.7, 10:1.0, 11:1.0,
12:1.0, 13:1.0, 14:1.0, 15:1.0, 16:0.8, 17:1.0, 18:0.8, 19:1.0, 22:1.0, 23:1.0, 24:1.0, 28:0.6, 101:1.0}
# "weather"列を0から1の範囲に変換
df["weather"] = df["weather"].astype("int").map(lambda x: w_dic[x])
欠損値を確認すると、気温と湿度に欠損があります。
時系列データなので直前のデータで補完することとし、
また湿度は0.**の表記に直しておきます。
#欠損値を直前の値で補完
df = df.fillna(method="pad")
df["weekday"] = df["weekday"].astype("object")
df["humidity"] = df["humidity"].map(lambda x : int(x)/100)
ここで再度データの特徴量を観察しておきます。
df["humidity"].plot(figsize=(30,3))
df["temperature"].plot(figsize=(30,3))
df["kw"].plot(figsize=(30,3))



気温も湿度も季節に沿って変動しているように見えますが、
湿度は1.0が最大のため、グラフ上辺に少し違和感があります。
3-3. 学習用データフレーム作成
ここからはモデルの学習に使うデータ形式に合わせて、
データフレームの変換作業を行っていきます。
まずは学習に不要な特徴量を捨てて、
先に訓練データとテストデータに分割しておきます。
# "date", "time"を落とす
df = df.iloc[:, 2:]
# "kw"をtargetに、他をfeatureに
feature = df.iloc[:, 2:]
target = df.iloc[:, 0]
# 全体の2割をtestデータとして分割
train_size = round(feature.shape[0] * 0.8)
train_x = feature.iloc[:train_size, :]
test_x = feature.iloc[train_size:, :].reset_index(drop=True)
train_y = target.iloc[:train_size]
test_y = target.iloc[train_size:].reset_index(drop=True)
各カラムの値を0から1の値に変換したのち、
モデルに渡すためにデータ型をfloat32に変換しておきます。
from sklearn.preprocessing import MinMaxScaler
mms_x = MinMaxScaler()
mms_x.fit(train_x.iloc[:, 4:])
train_x.iloc[:, 4:] = mms_x.transform(train_x.iloc[:, 4:])
test_x.iloc[:, 4:] = mms_x.transform(test_x.iloc[:, 4:])
mms_y = MinMaxScaler()
mms_y.fit(train_y.values.reshape(-1,1))
train_y = mms_y.transform(train_y.values.reshape(-1,1))
test_y = mms_y.transform(test_y.values.reshape(-1,1))
train_x = train_x.astype(np.float32)
test_x = test_x.astype(np.float32)
この時点でtrain_xとtrain_yは以下のようになっています。
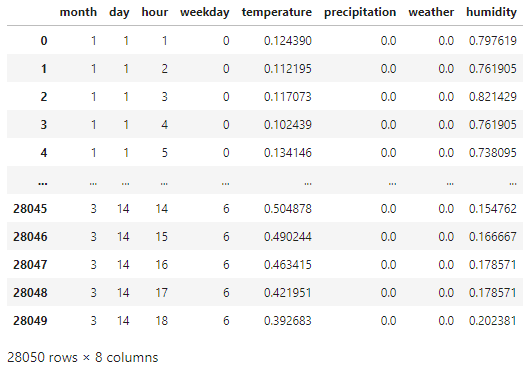
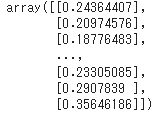
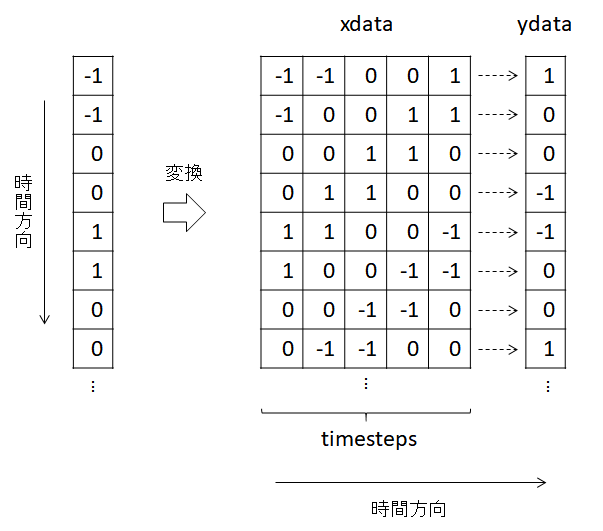
今回使用するモデルの学習では数個の連続したデータを参照し、
次のデータを予測するようアルゴリズムになっているため、
データを以下イメージのような形に変換する必要があります。
Kerasを使ったRNN, GRU, LSTMによる時系列予測
https://helve-blog.com/posts/python/keras-recurrent-neural-network/
今回はまず最初に6時間分のデータを参照して学習するように、
6件のデータを1つのまとまりとして処理します。
# 前6時間分のデータを参照する
timesteps = 6
data_x = []
xarr = np.array
for i in range(timesteps, train_x.shape[0]):
xset = []
for j in range(train_x.shape[1]):
d = train_x.iloc[i-timesteps:i, j]
xset.append(d)
xarr = np.array(xset).reshape(timesteps, train_x.shape[1])
data_x.append(xarr)
x_train = np.array(data_x)
# 6件目以降のデータを目的変数に
y_train = train_y[timesteps:]
#testデータも同様に変換
data_x = []
xarr = np.array
for i in range(timesteps, test_x.shape[0]):
xset = []
for j in range(test_x.shape[1]):
d = test_x.iloc[i-timesteps:i, j]
xset.append(d)
xarr = np.array(xset).reshape(timesteps, test_x.shape[1])
data_x.append(xarr)
x_test = np.array(data_x)
# 6件目以降のデータを目的変数に
y_test = test_y[timesteps:]
この時点で学習用データを確認しておくと、
["データ数", "timesteps", "特徴量数"]の3次元 になっています。

4. モデル作成/学習
4-1. ベンチマーク
まずは今回の分析精度のベンチマークとして、
簡単なRNNのモデルを構築して学習、予測してみます。
また今回は実装の手軽さ、コードの見やすさから
kerasを用いてRNN等のモデルを実装していきます。
ユニット数64のRNNモデル で学習し、その結果をmatplotで可視化します。
%%time
from keras.models import Sequential
from keras.layers import Dense, LSTM, SimpleRNN, GRU
from keras.layers import Dropout
from tensorflow.keras.callbacks import EarlyStopping
neuron = 64
actfunc = "tanh"
dropout = 0.2
epochs = 300
model_RNN_64 = Sequential()
model_RNN_64.add(SimpleRNN(neuron, activation=actfunc, batch_input_shape=(None, timesteps, x_train.shape[2]), return_sequences=False))
model_RNN_64.add(Dropout(dropout))
model_RNN_64.add(Dense(1, activation="linear"))
model_RNN_64.compile(loss="mean_squared_error", optimizer="adam")
early_stopping = EarlyStopping(monitor='val_loss', min_delta=0.0, patience=3)
history_RNN_64 = model_RNN_64.fit(x_train, y_train, batch_size=128, epochs=epochs, validation_split=0.2, callbacks=[early_stopping])
plt.figure(figsize=(15,8))
plt.plot(history_RNN_64.history['loss'], label='Train Loss')
plt.plot(history_RNN_64.history['val_loss'], label='valid Loss')
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epochs')
plt.legend(loc='upper right')
plt.show()
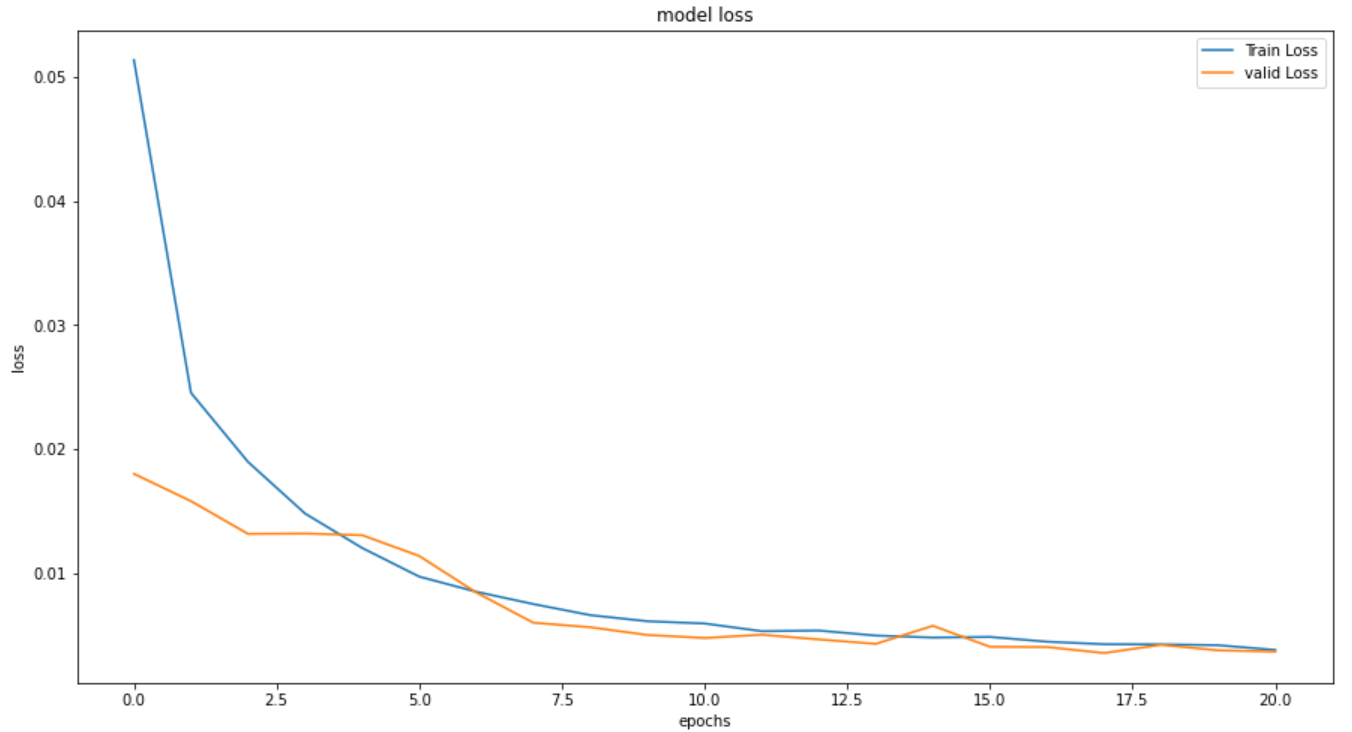
学習は 26.5秒 、エポック数は 21回 で収束しました。
このモデルでテストデータを予測して評価指標を出します。
y_test_pred_RNN_64 = model_RNN_64.predict(x_test)
y_test_pred_RNN_64 = mms_y.inverse_transform(y_test_pred_RNN_64)
y_t = mms_y.inverse_transform(y_test)
RNN_RMSE_64 = np.sqrt(mean_squared_error(y_t, y_test_pred_RNN_64))
RNN_MAE_64 = mean_absolute_error(y_t, y_test_pred_RNN_64)
RNN_MAPE_64 = mean_absolute_percentage_error(y_t, y_test_pred_RNN_64)
# 指標出力
print('RMSE:')
print(RNN_RMSE_64)
print('MAE:')
print(RNN_MAE_64)
print('MAPE:')
print(RNN_MAPE_64)

まだ比較対象がないので評価は不明ですが、
電気使用量が 「平均:3,238、標準偏差:667」 なので、
RMSEの値はそれほど悪い結果ではなさそうです。
#テストデータ(青)と予測(黄色)を描画
plt.figure(figsize=(30,8))
plt.plot(y_t, c="b")
plt.plot(y_test_pred_RNN_64, c="y")
plt.show()
# 後ろから2週間分(24*7*2)のデータだけ描画
plt.figure(figsize=(30,8))
plt.plot(y_t[-336:], c="b")
plt.plot(y_test_pred_GRU[-336:], c="y")
plt.show()
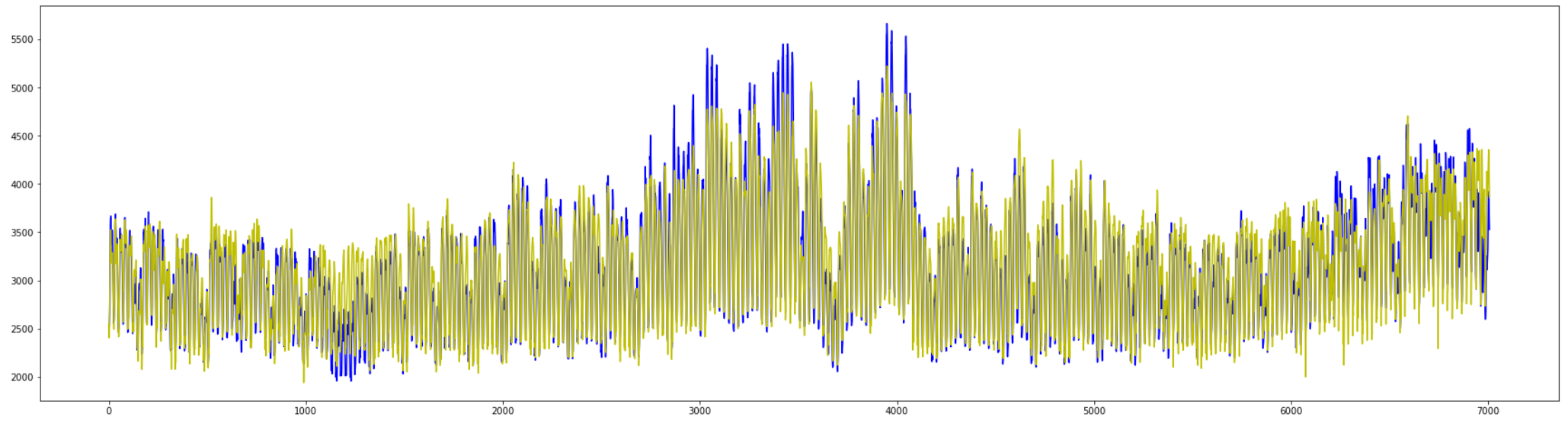
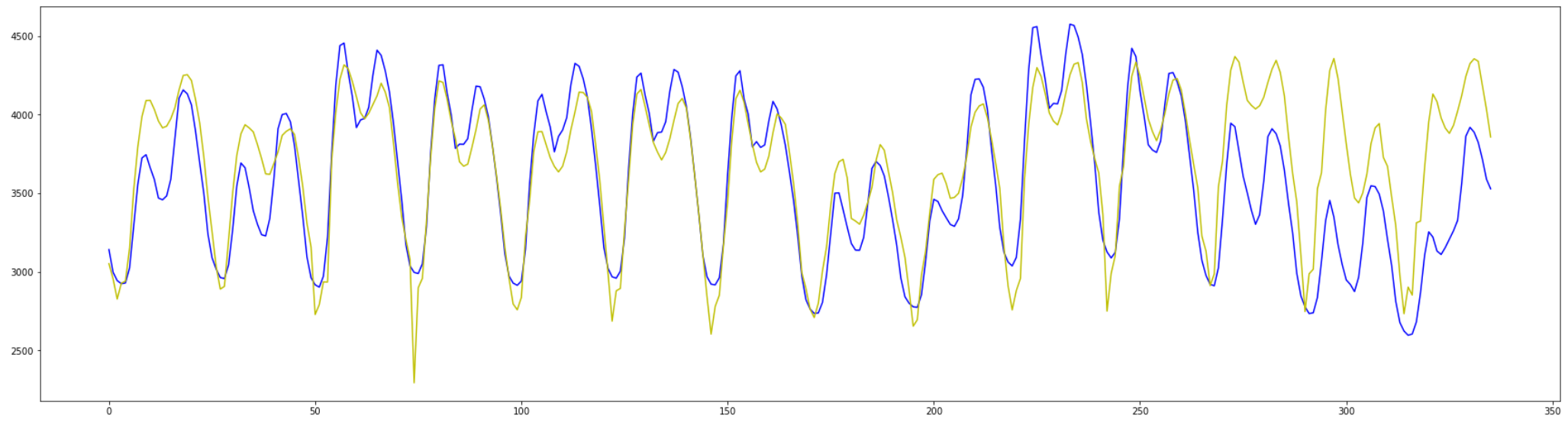
全体の大きな傾向は掴めていそうですが、
ところどころ上下の変動で外れている期間が見られます。
4-2. GRU/LSTMの比較
RNNの実装と同様にGRUとLSTMを実装します。
モデルの構成はRNNとまったく同じです。
4-2-1. GRU
まずはGRUの結果について見ていきます。
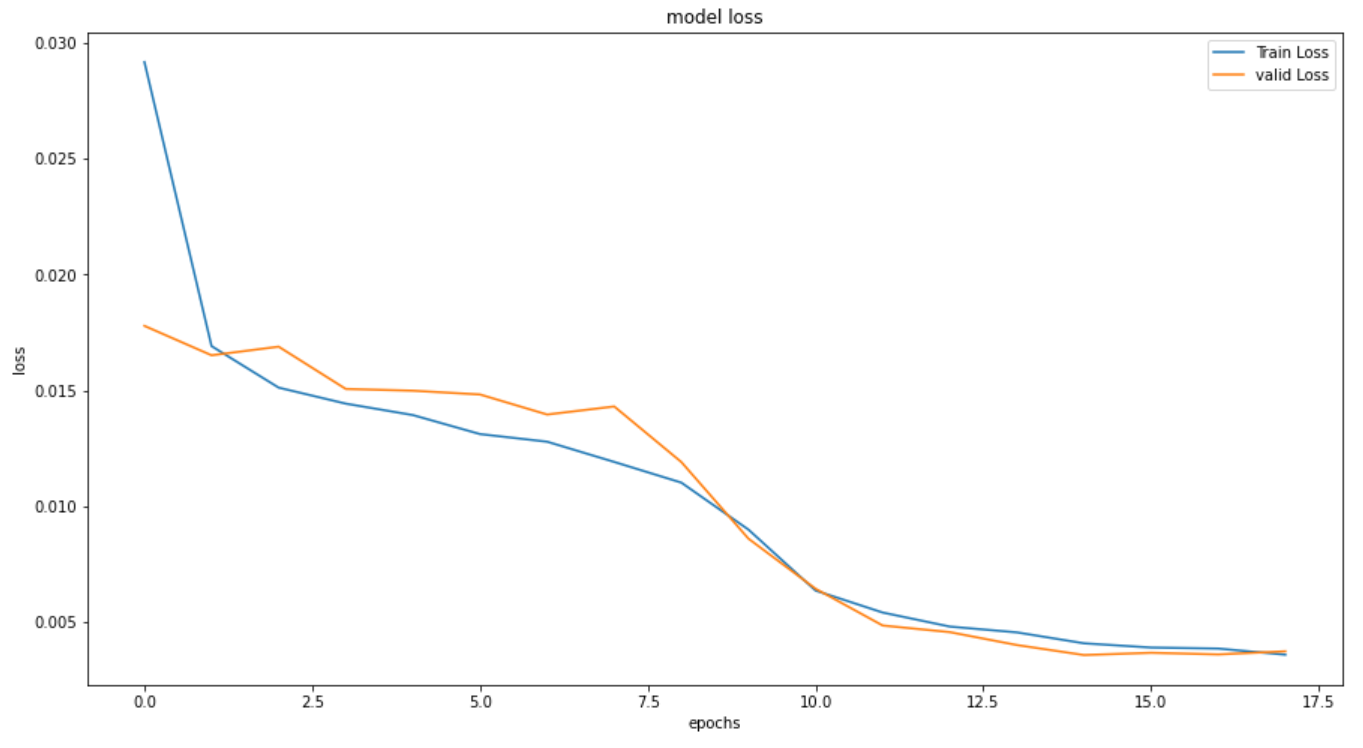
エポックは 18回 で順調に学習しています。
しかしGRUの学習には 42.5秒 かかり、
RNNの35秒からは10秒弱、時間が伸びています。

RMSEを含む全ての評価指標において改善が見られます。
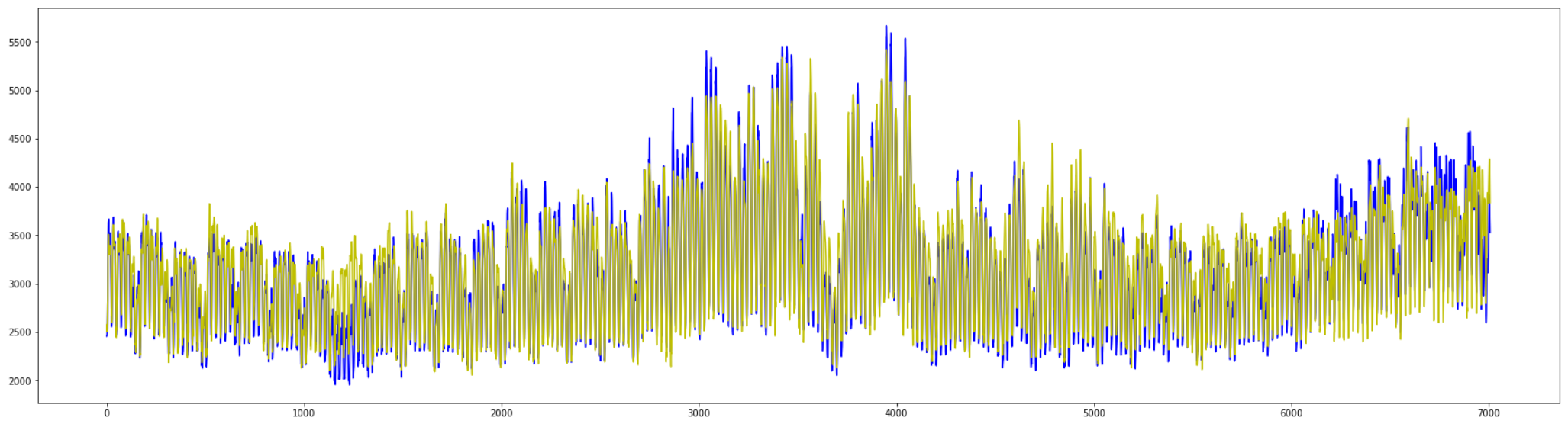
こちらもRNN同様、全体の変化はおおまかに捉えています。
4-2-2. LSTM
次にLSTMの結果です。
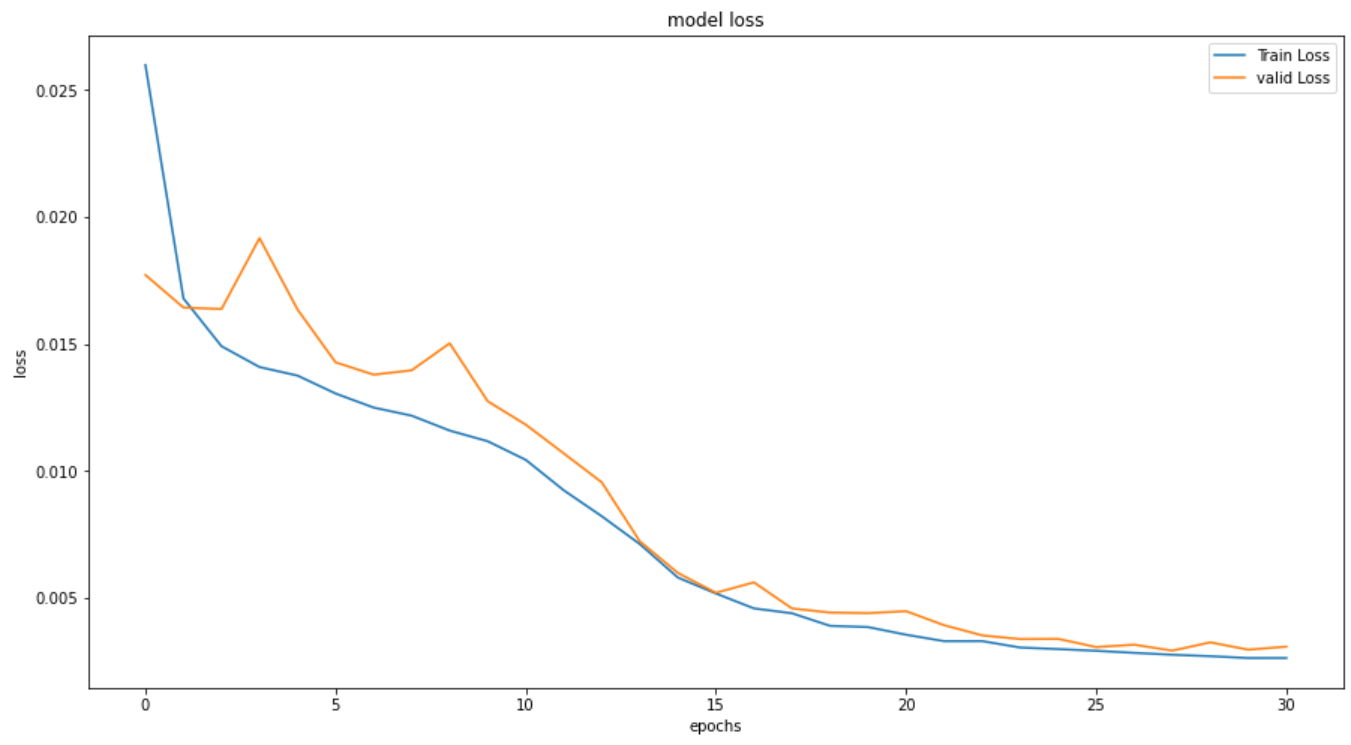
エポック数は 31回 で、学習時間は 76秒 でした。
GRUよりもさらに30秒ほど伸びています。

評価指標も全てGRUから改善されています。
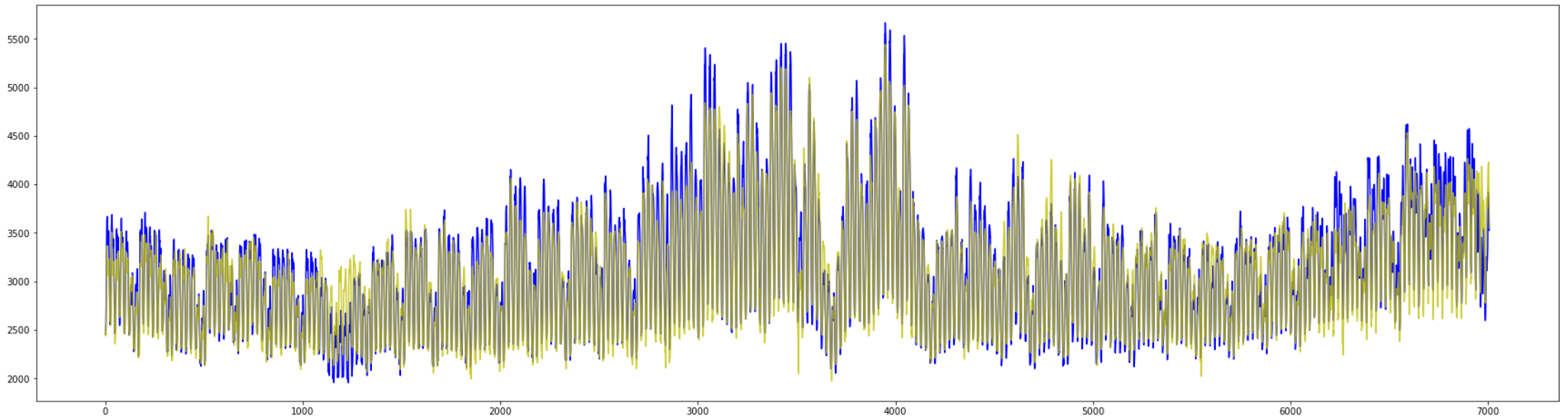
全体の予測に関しても同様の傾向です。
ただ何となく全体の振れ幅が小さいようにも見えます。
4-3. アーキテクチャによる比較
次にLSTMのアーキテクチャを変更して比較していきます。
以下の4つのパターンで構築します。
・ユニット数64(上記で実装したモデル)
・ユニット数128
・ユニット数256
・ユニット数128×2のLSTMスタッキングモデル
4-3-1. ユニット数128
まずは ユニット数128個 のモデルです。
%%time
neuron = 128
actfunc = "tanh"
dropout = 0.2
epochs = 300
model_LSTM_128 = Sequential()
model_LSTM_128.add(LSTM(neuron, activation=actfunc, batch_input_shape=(None, timesteps, x_train.shape[2]), return_sequences=False))
model_LSTM_128.add(Dropout(dropout))
model_LSTM_128.add(Dense(1, activation="linear"))
model_LSTM_128.compile(loss="mean_squared_error", optimizer="adam")
early_stopping = EarlyStopping(monitor='val_loss', min_delta=0.0, patience=3)
history_LSTM_128 = model_LSTM_128.fit(x_train, y_train, batch_size=128, epochs=epochs, validation_split=0.2, callbacks=[early_stopping])
こちら上記同様に結果を表示していきます。
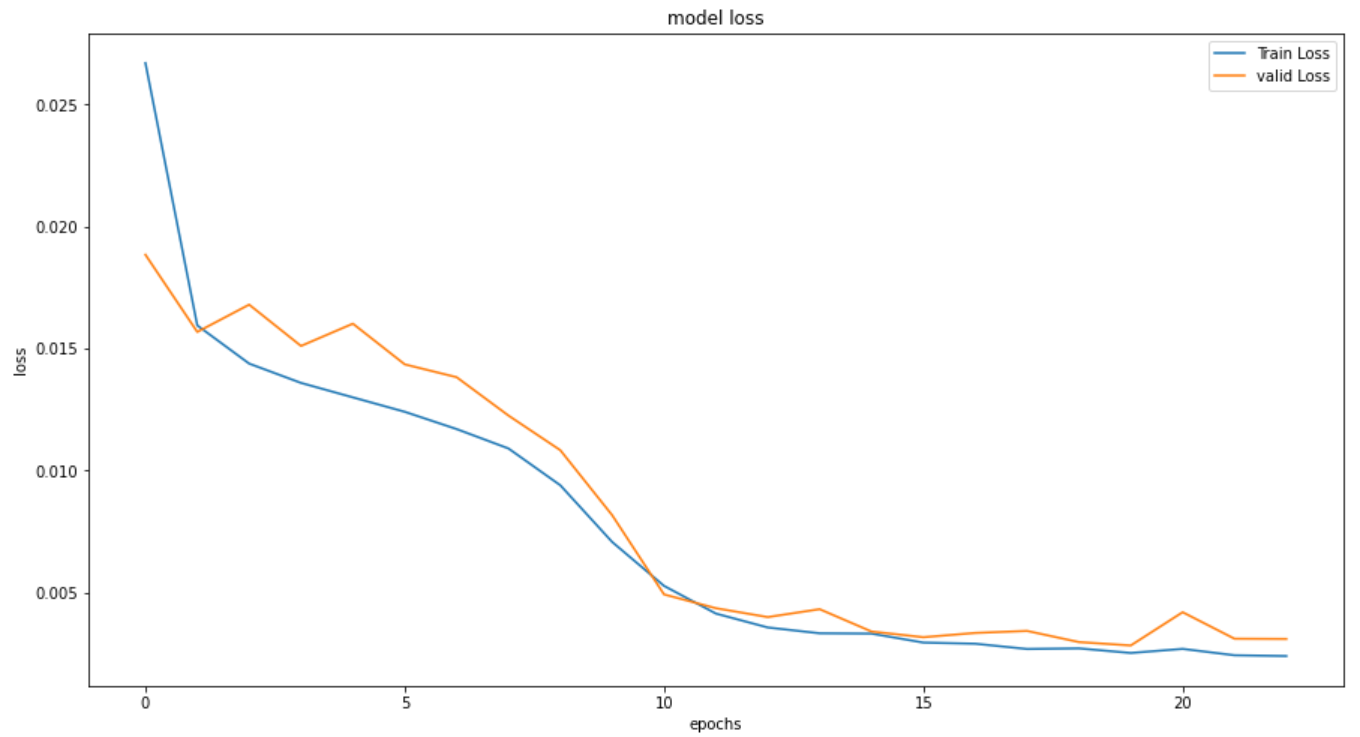
エポック数は 23回 で、時間は 75秒 でした。
収束が早かったため、計算時間は変化なしでした。

RMSEは改善していますが、他2つは悪化しています。
この結果の差は、乱数による誤差の範囲かと思われます。
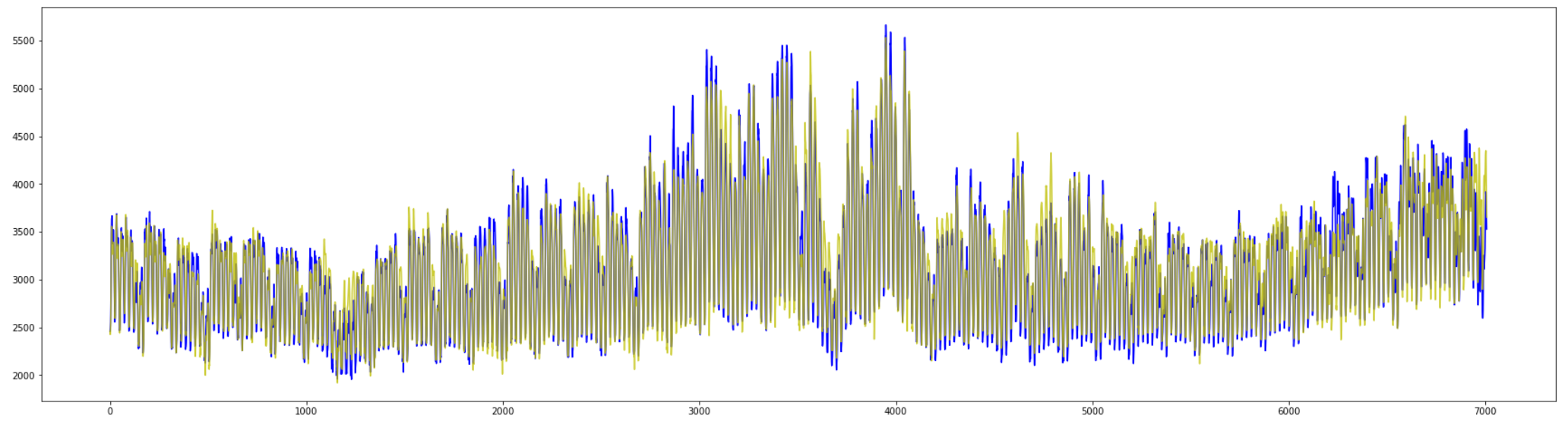
全体の予測としては上下の振れ幅は適応しているように見えます。
中間の上昇幅や、最後の1割ほどの変化がうまく予測できません。
4-3-2. ユニット数256
同様に ユニット数を256 にしてモデルを構築します。
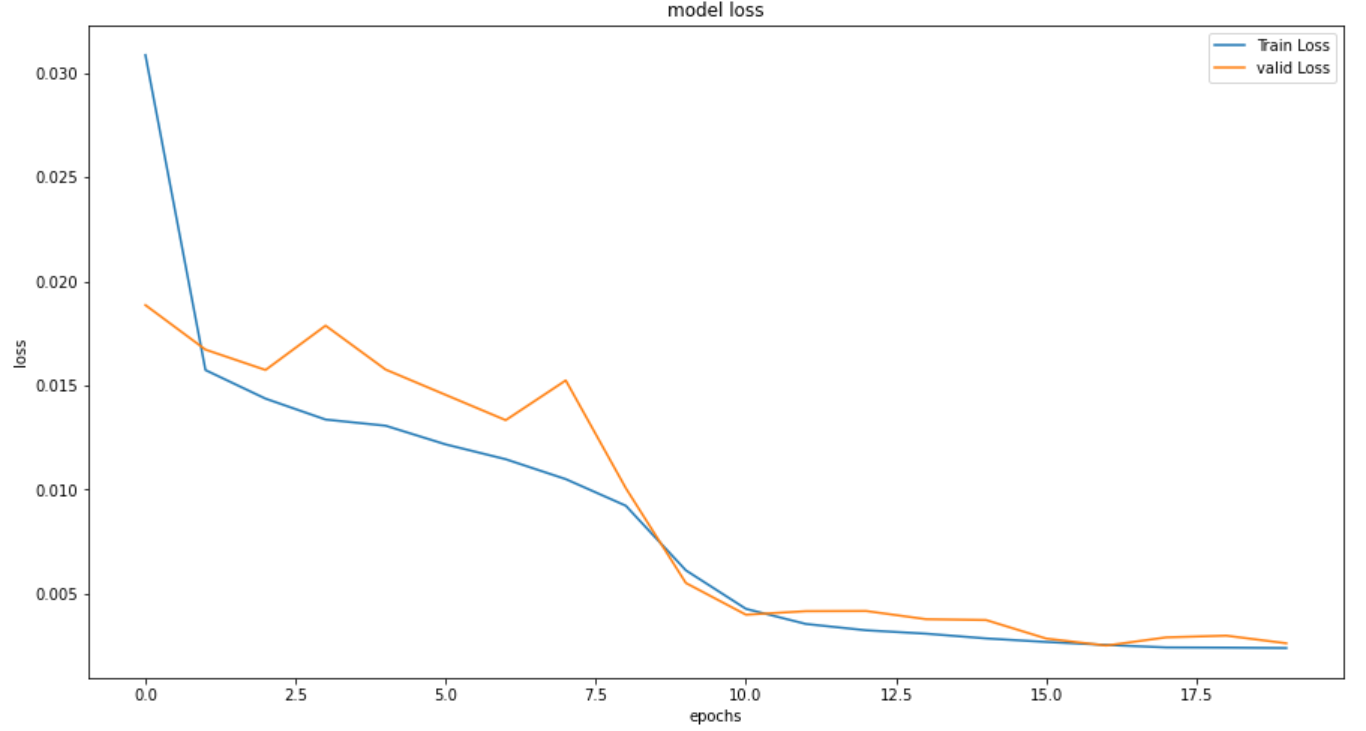
10エポックあたりから精度が落ち着いています。
最終エポックは20 で、計算時間は 102秒 でした。
順当に計算時間は伸びてきています。

RMSEは悪化しましたが、MAEとMAPEは改善しました。
計算コストに対する改善幅としては微妙な気もします。
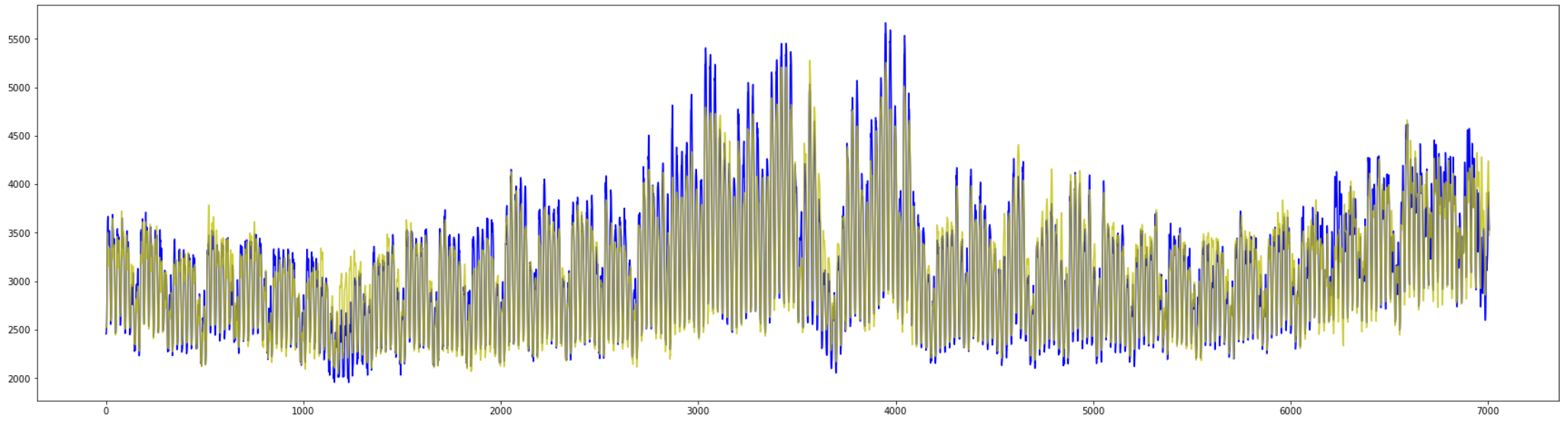
全体の予測はユニット数64の時と少し似ていて、
下に対する振れ幅が小さいような予測になっています。
中間時期の上に対する振れ幅は大きく外しています。
4-3-3. スタッキングモデル
最後に ユニット数126のLSTM層を2回繰り返し て
スタッキングモデルを構築してみます。
%%time
neuron = 128
actfunc = "tanh"
dropout = 0.2
epochs = 300
model_LSTM_stack = Sequential()
model_LSTM_stack.add(LSTM(neuron, activation=actfunc, batch_input_shape=(None, timesteps, x_train.shape[2]), return_sequences=True))
model_LSTM_stack.add(Dropout(dropout))
model_LSTM_stack.add(LSTM(128, activation=actfunc))
model_LSTM_stack.add(Dropout(dropout))
model_LSTM_stack.add(Dense(1, activation="linear"))
model_LSTM_stack.compile(loss="mean_squared_error", optimizer="adam")
early_stopping = EarlyStopping(monitor='val_loss', min_delta=0.0, patience=5)
history_LSTM_stack = model_LSTM_stack.fit(x_train, y_train, batch_size=128, epochs=epochs, validation_split=0.2, callbacks=[early_stopping])
1個目のLSTM層に同じように層を追加しています。
スタッキングを行う際はreturn_sequences=Trueを設定し、
出力が元の3次元と同じになるようにしています。
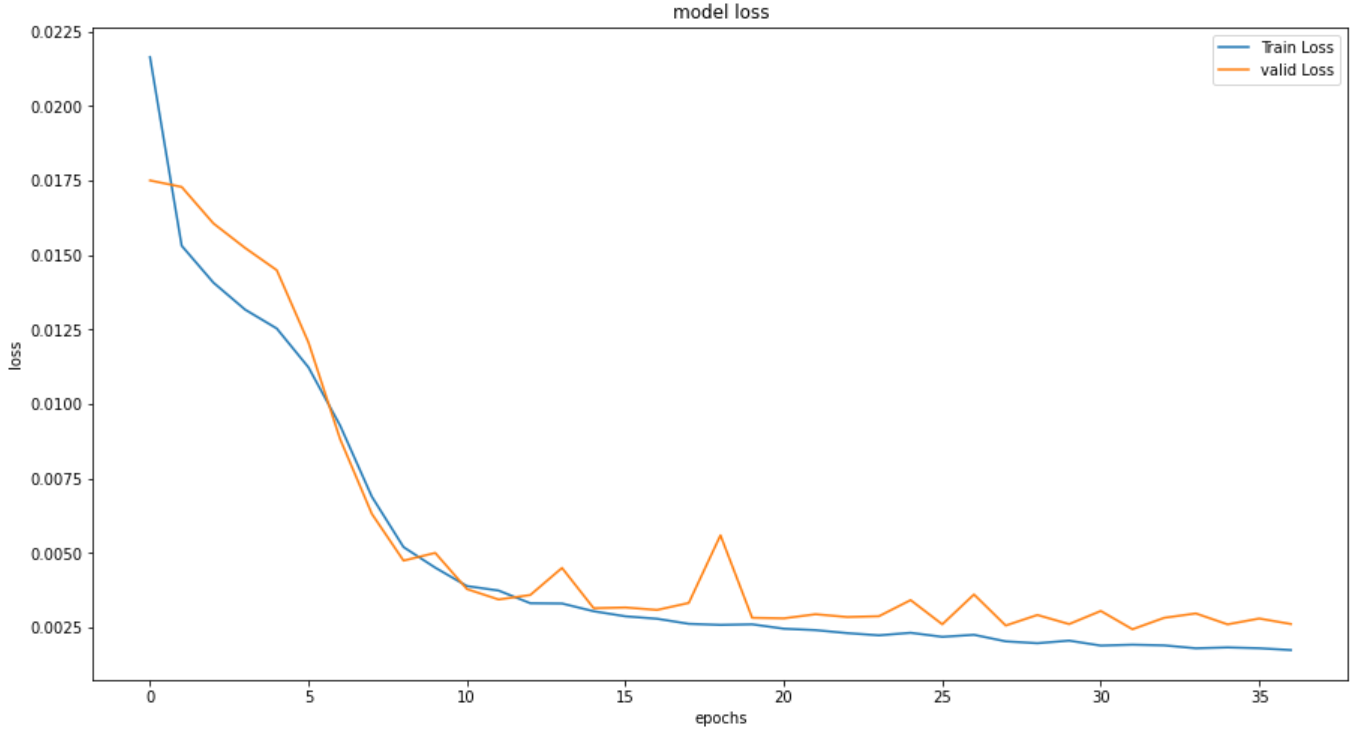
15エポックあたりから改善幅は小さくなっていますが、
最終的にエポック数 37回 まで進み、計算時間は 243秒 でした。

精度は全ての項目で改善が見られ、
今までで最も精度の高いモデルとなりました。
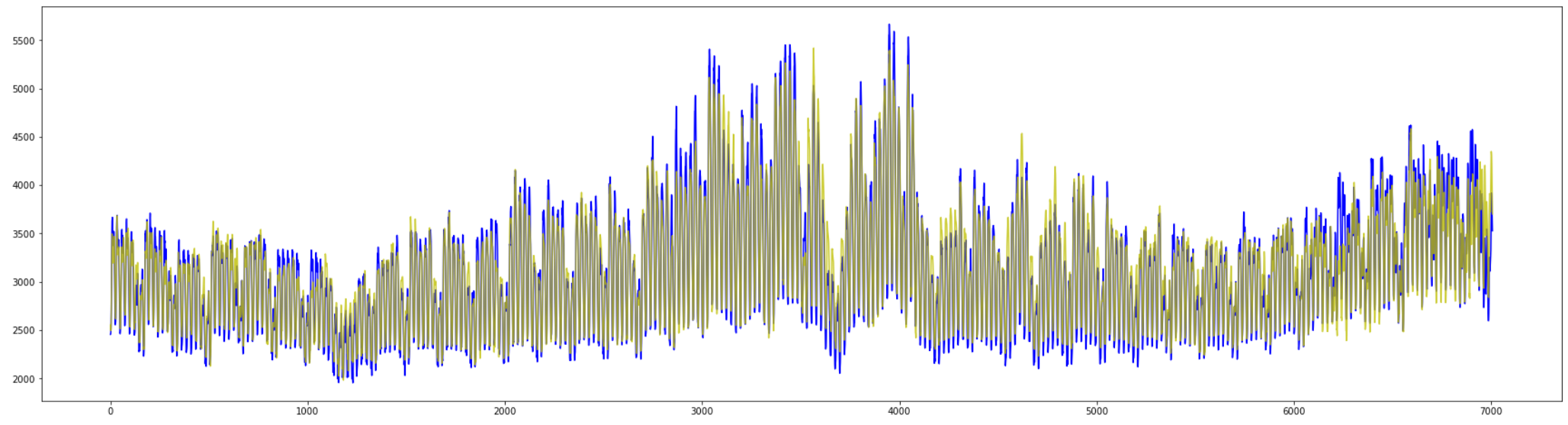
中間の期間の上下幅もうまく予測ができていますが、
いまだに最後の1割ほどの期間は外れ気味です。
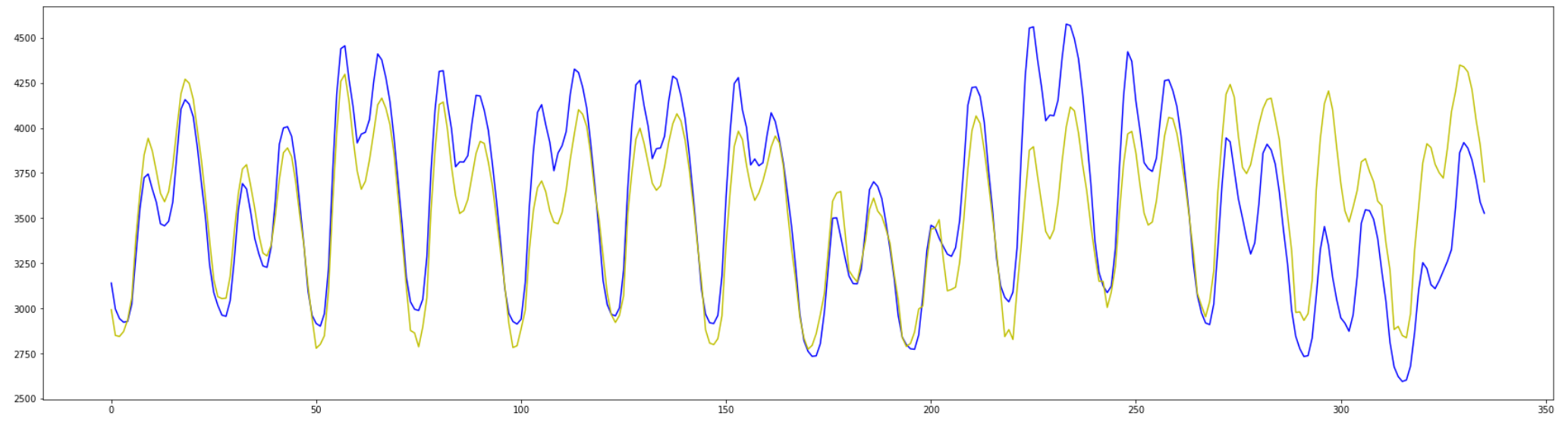
最後の2週間を見てみると変化の形は
それなりに高い精度で描画してくれています。
(青:観測した値 / 黄色:予測した値)
4-4. 結果の出力と観察
上記のようなモデル比較をRNN/GRUについても行い、
また timestepsを6から12,24に変更して 検証を行いました。
4-4-1. timesteps=6の場合
まずはtimesteps=6の結果一覧です。
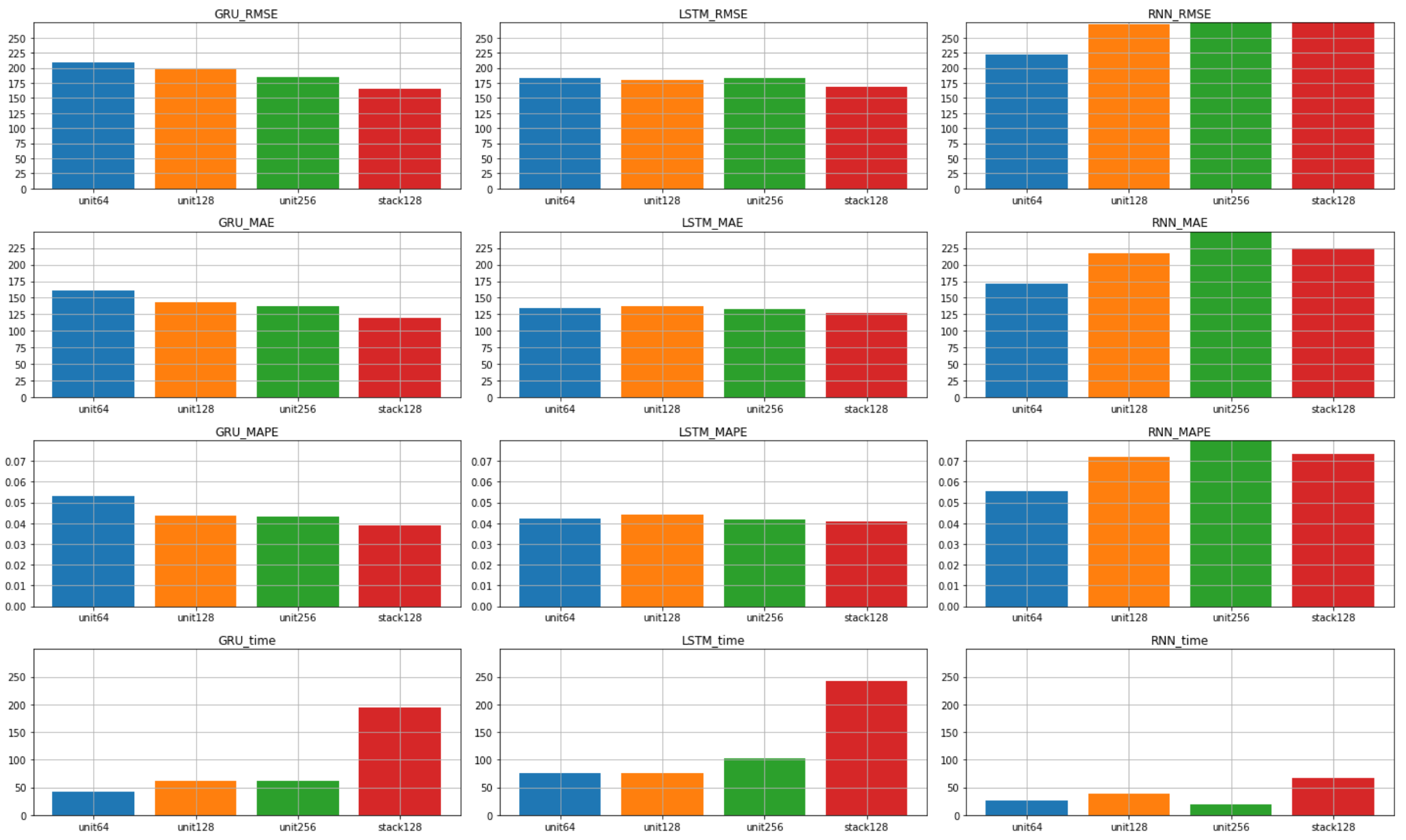
RNNはモデルを複雑にしても精度が上がらず、
おそらく勾配消失により学習が不可になっていました。
最終的に評価制度において最も精度が高かったのは
ユニット数126のGRUスタッキングモデル でした。
計算時間もLSTMと比べて短く、
学習の経過も安定していたように思います。
4-4-2. timesteps=12の場合
次にtimesteps=12の結果一覧です。
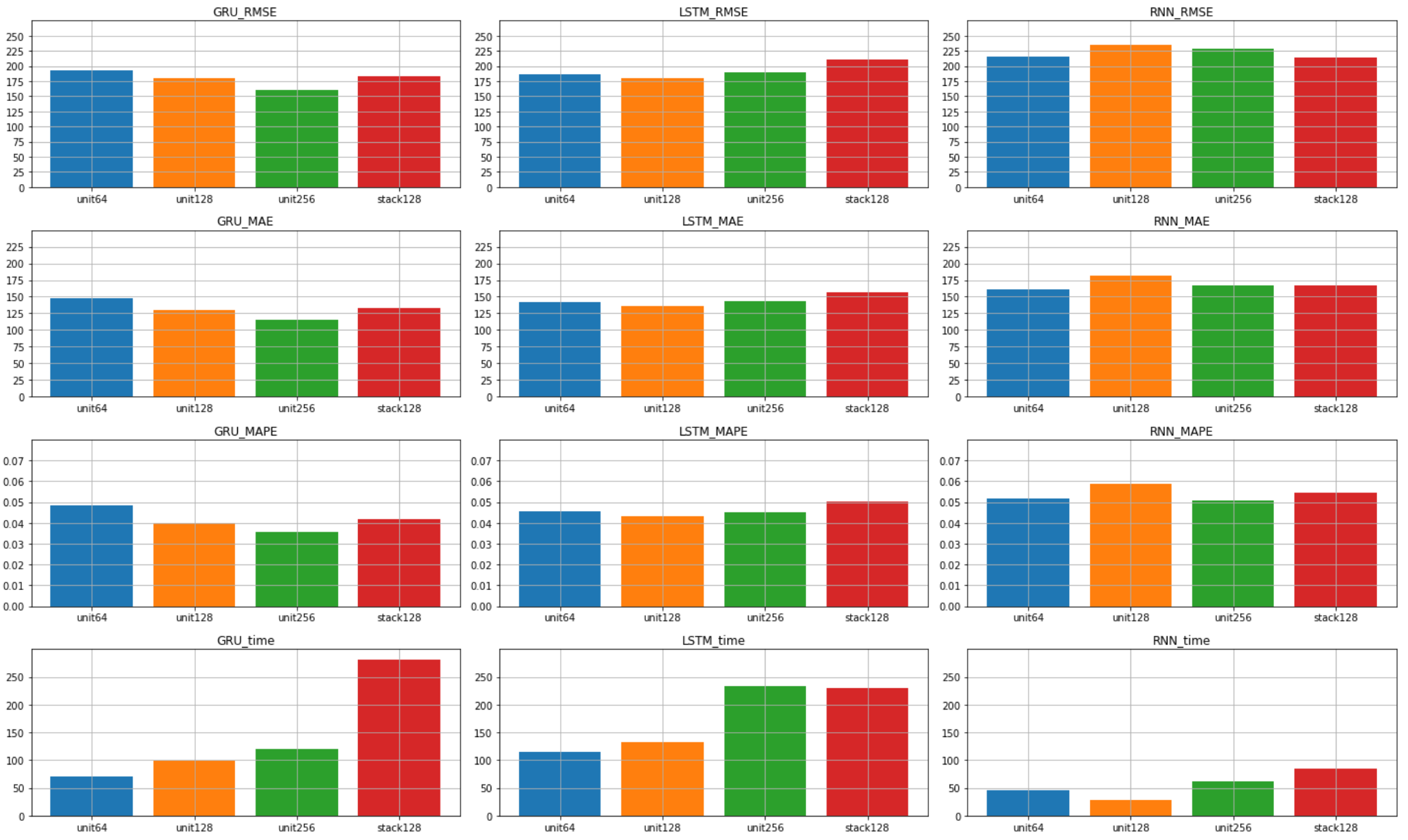
今度は ユニット数256のGRU の精度が良くなりました。
予測の精度自体もtimesteps=6の時よりも改善しています。
計算コストはtimesteps=12の方が多いはずですが、
収束までのエポック数に影響してか、
全体的に計算時間が少し短くなっています。
RNNについては精度がtimestepsによって
unit数128と256のモデルにおいて精度が大幅に改善しました。
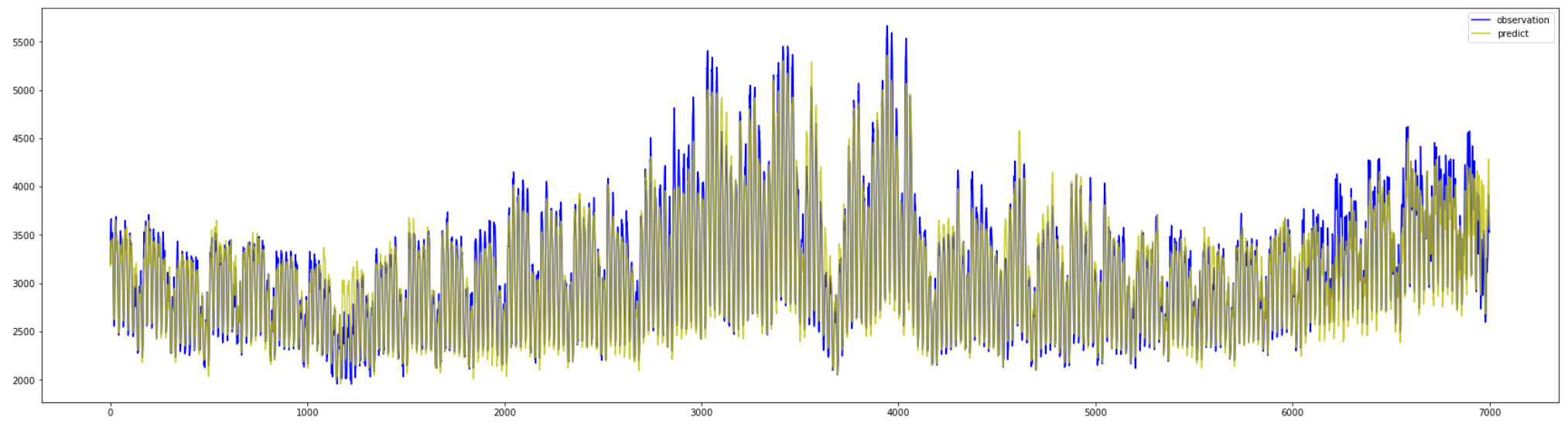
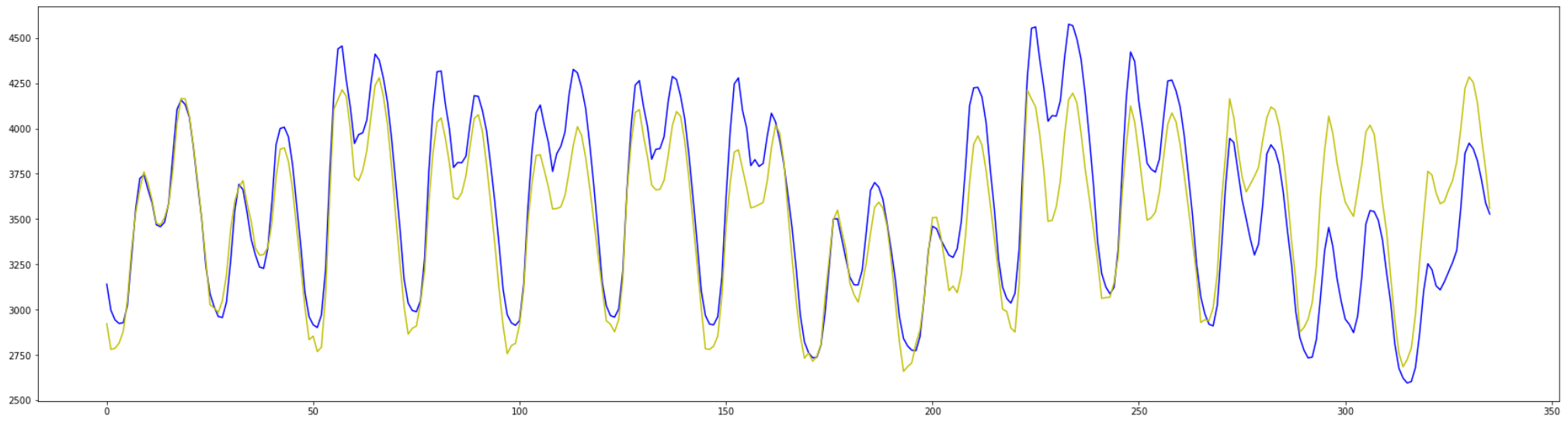
最終的に ユニット数256のGRU が最も精度が高かったので、
その予測のプロットをこちらに添付しておきます。
(青:観測した値 / 黄色:予測した値)
4-4-3. timesteps=24の場合
最後にtimesteps=24の結果の一覧を確認します。
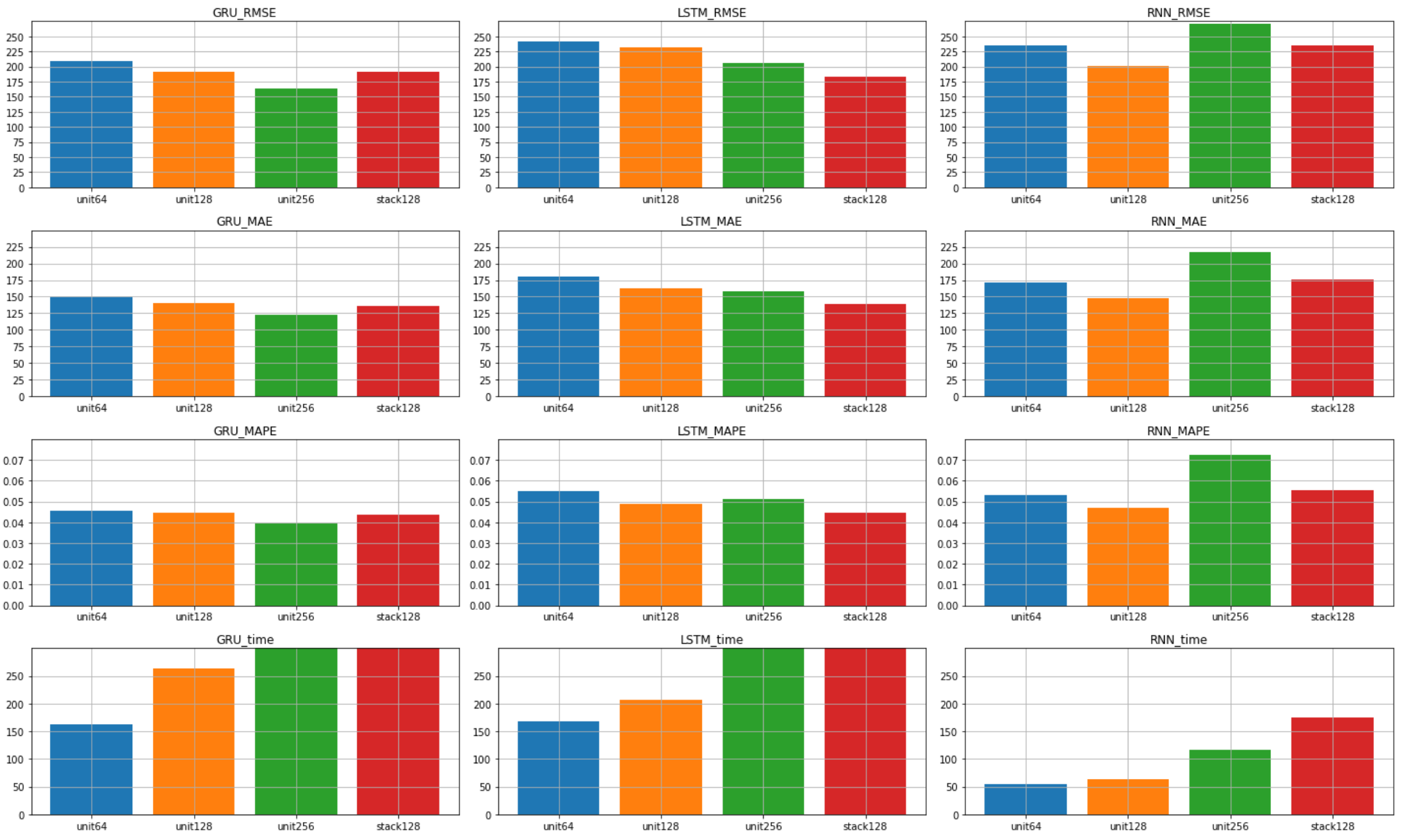
timesteps=6, 12と比較できるように
グラフのtickをあえて変更せずに表示しています。
この一覧の中で最も精度が良いのはGRU256ですが、
LSTMはモデルが複雑になるに連れて
精度が改善されていく傾向が見て取れます。
データサイズがより大きく、
参照する期間がより長い場合にはLSTMのモデルの
複雑さを増すことで精度が改善できるかも知れません。
しかし計算時間も大幅に伸びており、
LSTMのスタッキングでは800秒を超えていました。
計算コストと引き換えにはなりますが、
参照する期間を延ばしながら分析を行う場合には、
LSTM層をさらに追加するようなモデルの検討が必要 になりそうです。
5. 課題と所感
5-1. 今後の課題
本分析における今後の課題は以下の通りです。
・特徴量のバリエーションによる精度が未検証
・現状のモデルでは予測期間の天気情報がないと予測が不可能
・計算コストの高いモデルの検証が個人のマシンだと限界がある
特徴量による精度変化の検証は、
・天気, 気温, 湿度, 降水量の有無のパターンを検証
・祝日かどうかの特徴量を追加して検証
あたりを考えています。
未知の期間の予測については、
直近のデータから予測した直後の値をまた入力として受け取り、
それを繰り返すことで未来を予測 するモデルの作成を予定しています。
最後のマシンスペックの問題は特にチャレンジする予定はありませんが、
AWSやGCPを利用して、仮想マシン上で行うのが現実案かと思います。
5-2. 所感
今回初めてRNN/GRU/LSTMのモデルについて学習し、
電気需要の予測にて実装までチャレンジしてみました。
周期性のあるデータだったこともあり、
自分が予想していたよりは精度が良かったのが正直な感想です。
今回のチャレンジで次への課題も明確になったので、
今後は未来の値を予測するモデルの構築に挑戦してみたいです。
5-3. さいごに
最後まで記事を読んで下さりありがとうございました。
ぜひお気軽にコメントなどよろしくお願い致します。
次回のページ
参考ページ